复杂网络流行病传播模型 - SISISSIR(含实例)python

Posted 2022-04-11 司六米希

【复杂网络】流行病传播模型 - SI、SIS、SIR【python】

• 1. 流行病传播概念
• 2.流行病传播模型
• • 2.1 模型数据集
  • • 2.1.1数据集
    • 2.1.2数据导入及绘制
    • 2.1.3数据集网络图
  • 2.2 SI模型
  • • 2.2.1实现思路
    • 2.2.2 代码
    • 2.2.3结果
  • 2.3 SIS模型
  • • 2.3.1实现思路
    • 2.3.2代码
    • 2.3.3结果
  • 2.4 SIR模型
  • • 2.4.1实现思路
    • 2.4.2代码
    • 2.4.3结果

1. 流行病传播概念

• 易感态（Susceptible，S）：尚未感染疾病的个体；
• 感染态(Infected，I)：已经感染疾病且具有传染能力的个体；
• 恢复态(Recovered，R)：治愈后获得了永久免疫能力或者是因病死亡的个体

2.流行病传播模型

2.1 模型数据集

2.1.1数据集

数据集是由200个节点构成的关联图，可以类比理解为200个人的社区，每一个人都有自身的关系连接(称之为邻居节点)

2.1.2数据导入及绘制

代码👇

2.1.3数据集网络图

2.2 SI模型

在节点一旦从S 态变为I 态后，便永远处于I 态。用来描述那些染病后不可能治愈的疾病，或对于突然爆发尚缺乏有效控制的流行病

2.2.1实现思路

1. 创建S，I字典(用于存放正常节点+已被感染节点)
2. 初始化随机种子，并产生随机种子的列表存放在seed_list作为感染者集
3. 获取感染者的邻居【邻居节点会按一定概率被感染】
4. 于I字典【感染者】中增加被随机种子选中的新的感染者
   于S字典【正常者】中减少被随机种子选中的新的感染者
5. 更新新的正常者和感染者【计算存活率】
6. 直至正常者为0，程序结束

2.2.2 代码

详看【3完整代码】

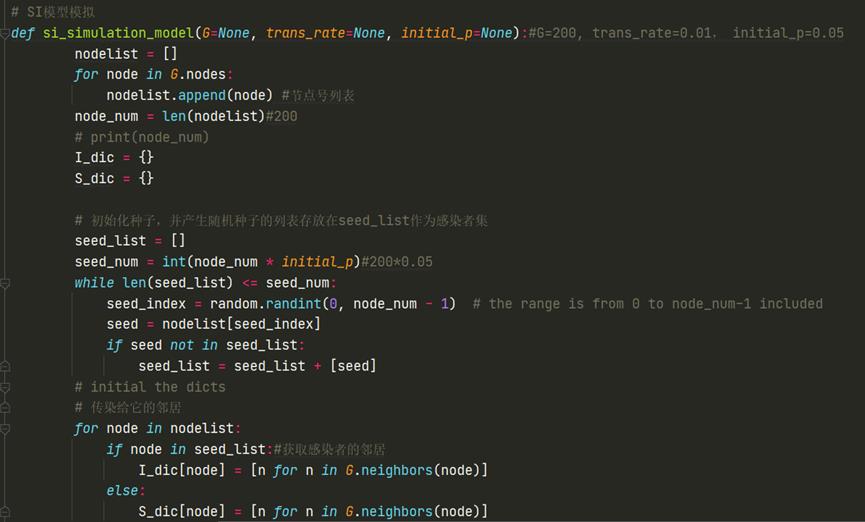
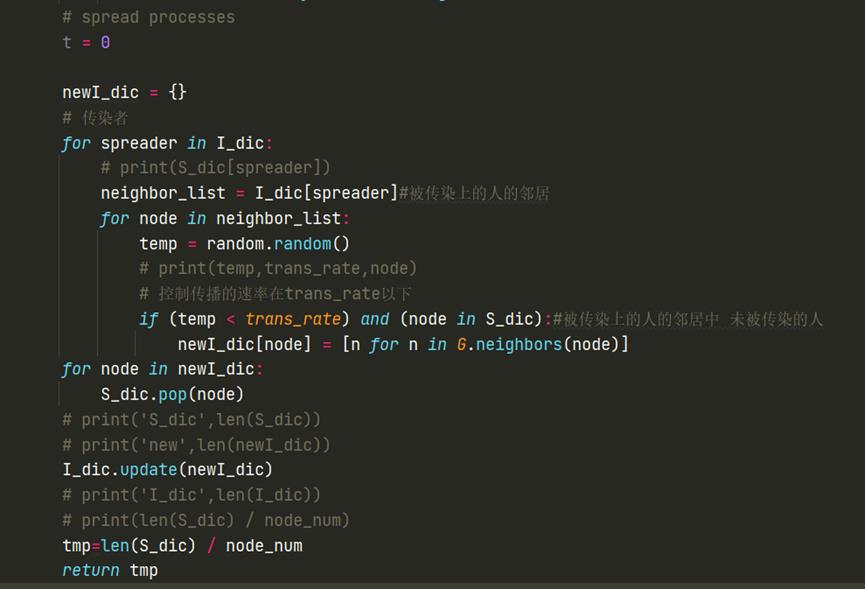
存活率计算👇

2.2.3结果

SI👇

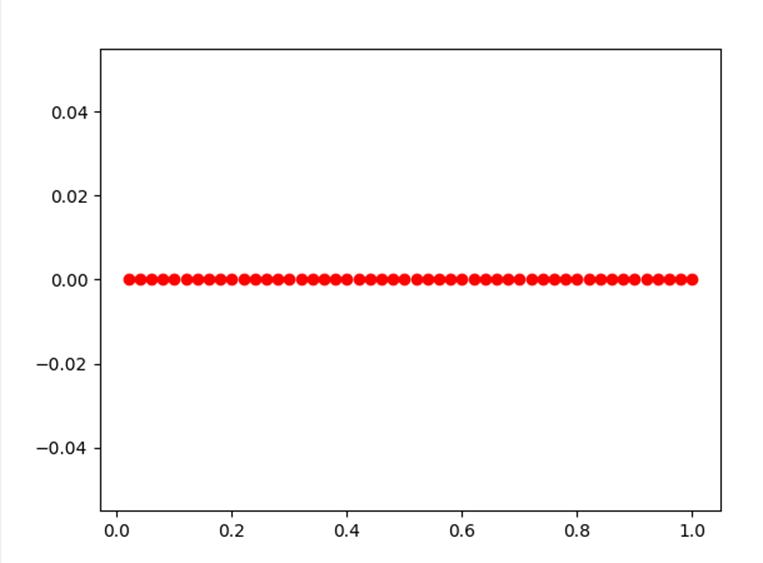
SI绘图改进👇
因为上图0.00是因为在while循环中只有S_dic全部被感染才会返回出来绘制图像，所以会导致无论循环多少次都会是以0.00作为最终结果返回，对此图像改成新的图像如下

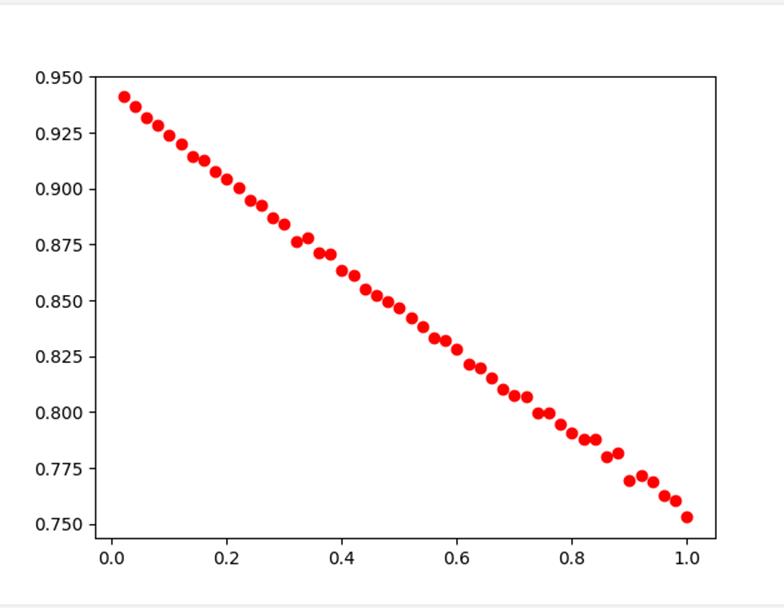
2.3 SIS模型

S 态的节点接触I 态的节点之后会以λ 的概率转换成I 态，同时，I态的节点也会以γ 的概率恢复成S 态

2.3.1实现思路

1. 在实现SI模型的思路基础上，增加一个recov_rate参数【recov_rate概率是感染者恢复正常】，实现I到S的转换
2. 更新新的正常者和感染者【计算存活率】

2.3.2代码

2.3.3结果

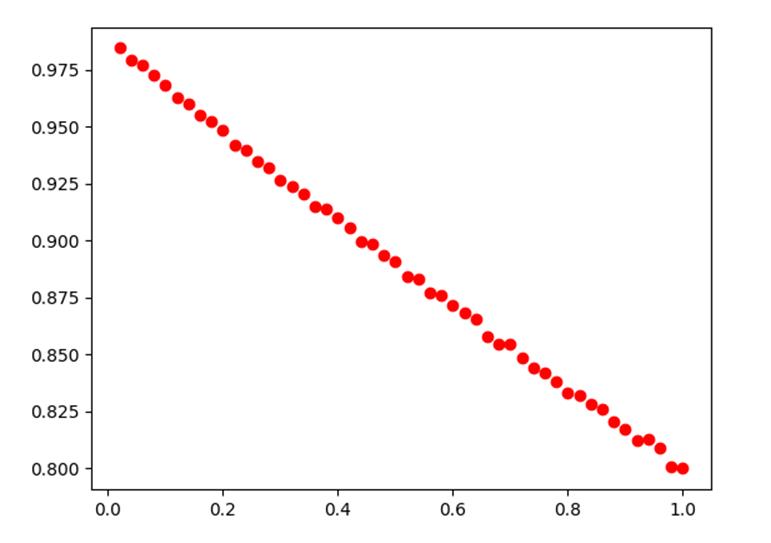
2.4 SIR模型

S 态的节点接触I 态的节点之后会以λ 的概率转换成I 态，I 态的节点会以γ 的概率转换成R 态

2.4.1实现思路

1. 在实现SI模型的思路基础上，增加一个recov_rate参数【此处的recov_rate概率是感染者转换为恢复态】，实现I到R的转换
2. 更新新的正常者、感染者以及恢复者【计算存活率】

2.4.2代码

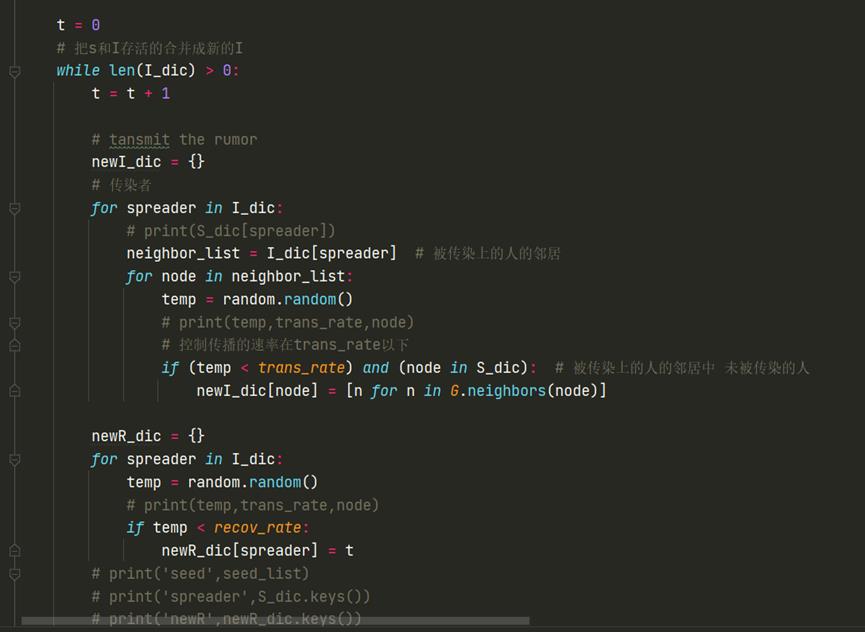
2.4.3结果