[机器学习与scikit-learn-36]：算法-分类-支持向量机-多项式预处理升维实现线性不可分分类的代码示例

Posted 2022-03-30 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123802467

---

目录

前言：

第1章 用线性向量机实现非线性分类的基本思想

第2章 代码示例

2.1 步骤1：导入库

2.2 步骤2：导数数据集

2.3 步骤3：构建待多项式预处理的复合模型并进行模型训练

2.4 步骤4：可视化训练效果

---

前言：

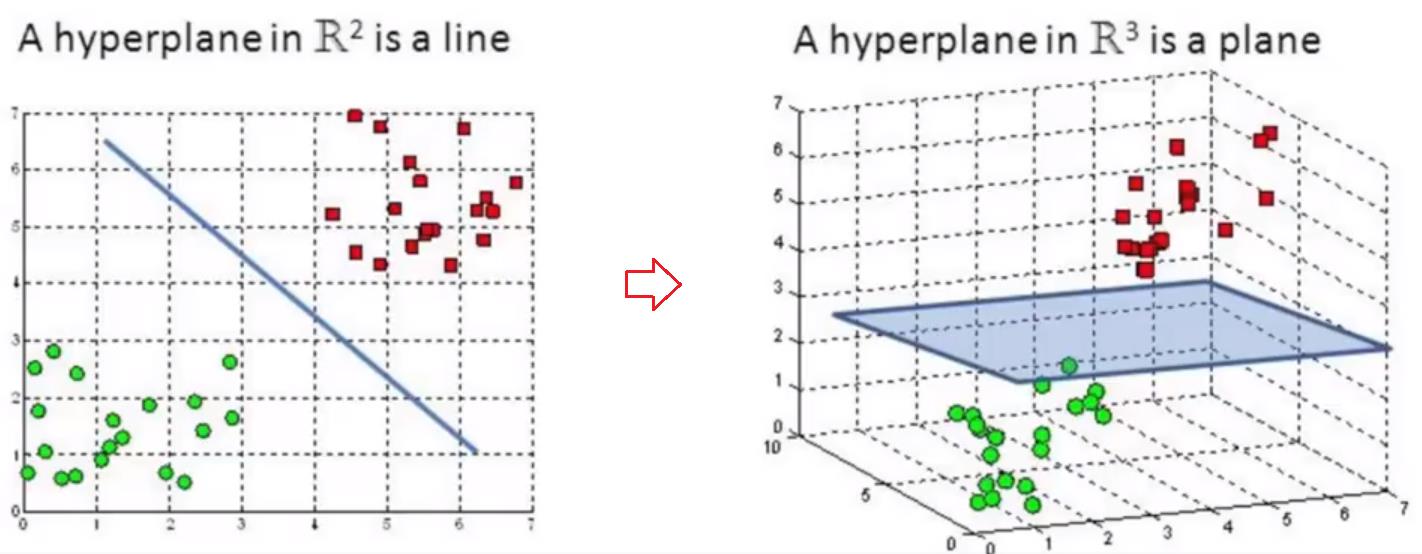
很多时候，原始的分类数据，是线性不可分的，如下图所示：

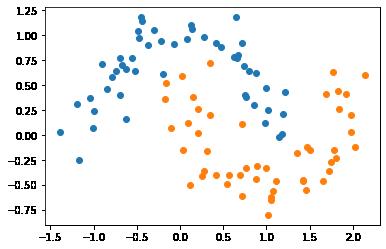
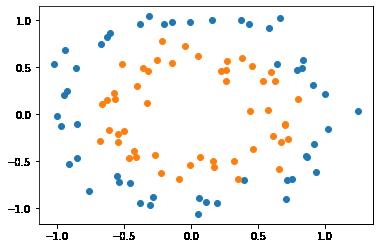
支持向量机可以通过多种方式实现对线性不可分数据的分类。

（1）多项式数据预处理=》数据特征维度的升维

（2）核函数

本文探讨代码展示多项式数据预处理的方法。

第1章 用线性向量机实现非线性分类的基本思想

基本思想是通过多项式数据预处理，实现对原始数据的特征进行升维，在高纬度空间进行线性分类。

（1）线性不可分数据

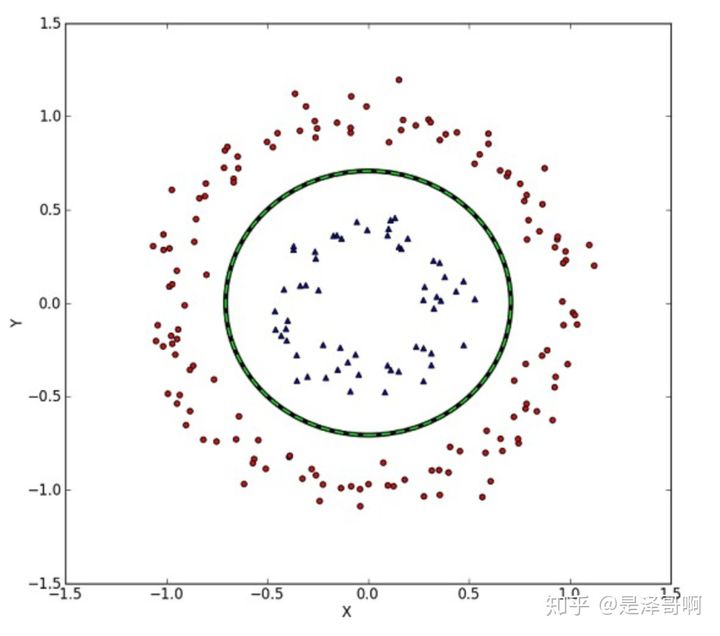
（2）升维后的数据

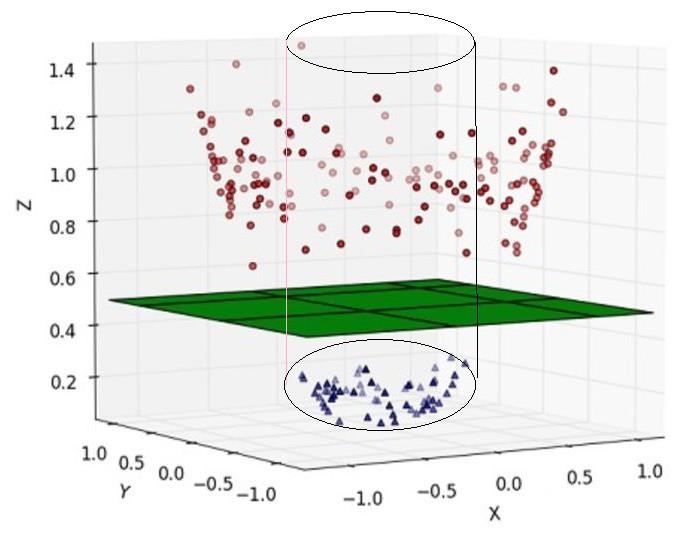
（3）详细的原理参考：

[机器学习与scikit-learn-33]：算法-回归-通过PolynomialFeatures实现数据的升维_文火冰糖的硅基工坊的博客-CSDN博客作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客本文网址：目录前言：第1章 低纬度空间（二维）的非线性样本数据分布第2章 用线性模型拟合拟合非线性分布数据的困难第3章 对非线性分布数据进行升维（三维空间）3.1 什么是升维3.2 升维的本质3.3sklearn中升维方法第4章 在高纬度实现对低纬度非线性分布数据的线性拟合前言：我们常听说降维打击，这是指，在高维度空间可以轻松地实现对低维度空间的打击。本文讲展示这里...https://blog.csdn.net/HiWangWenBing/article/details/123591729

第2章 代码示例

2.1 步骤1：导入库

import numpy as np
import matplotlib.pyplot as plt

2.2 步骤2：导数数据集

# 导入数据集
from sklearn import datasets

# nosize: 设定噪声数据，值越大，噪声越大
# noise = 0.01， 0.1

#x, y = datasets.make_moons(noise=0.1)

#sklearn.datasets.make_circles(n_samples=100, shuffle=True, noise=None, random_state=None, factor=0.8)
# factor：0 < double < 1 默认值0.8, 内外圆之间的比例因子

X, y = datasets.make_circles(noise=0.1, factor=0.6)
print(X.shape)
print(X[0])   # (X1,X2) 二维数据
print(y.shape)
print(y[0])  #标签数据为0或1

# 可视化数据集
plt.scatter(X[y==0,0], X[y==0,1]) # 标签为0的数据
plt.scatter(X[y==1,0], X[y==1,1]) # 标签为1的数据
plt.show()

(100, 2)
[-0.08955658  1.13702652]
(100,)

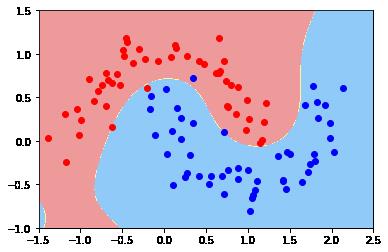
（1）make_moons（）数据集

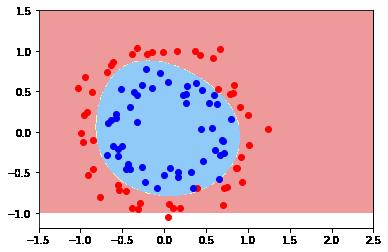
（2）make_circles（）数据集

2.3 步骤3：构建待多项式预处理的复合模型并进行模型训练

本文是通过数据预处理来实现数据的升维，从而可以使用线性模型能够处理原始的非线性可分数据。

# 创建带有数据预处理pipeline复合模型
# 这个复合模型有原始数据输入和整体输出
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline  import Pipeline

def CreatePolynomialSVC(degree, C):
    return Pipeline([
        # 把输入数据进行升维度
        ("poly", PolynomialFeatures(degree=degree)), 
        ("std_scaler", StandardScaler()),
        ("linearSVC", LinearSVC(C=C))
    ])

## C: 控制线性拟合的容错能力
## degree: 非线性的次方数，degree=2：二次抛物线；degree=3：三次方
poly_svc = CreatePolynomialSVC(degree=4, C=1.0)
poly_svc.fit(X,y)
print(poly_svc)

Pipeline(steps=[('poly', PolynomialFeatures(degree=4)),
                ('std_scaler', StandardScaler()), ('linearSVC', LinearSVC())])

2.4 步骤4：可视化训练效果

def plot_boundary(model, axis):
    # 在X轴上取100点
    x_line = np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100))
    # 在Y轴上取100点
    y_line = np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100))
    # 用x_line，y_line构建网格点向量
    x0, x1 = np.meshgrid(x_line, y_line)
    # 构建网格向量X
    X_new = np.c_[x0.ravel(), x1.ravel()]
    
    # ！！！！！！！！！！！！！！！！！！！！！
    # 对网格平面上的所有点进行预测,输出各自的类别0或1
    y_predict = model.predict(X_new)
    print("y_predict.shape",y_predict.shape);
    # zz的输出是0或1
    zz = y_predict.reshape(x0.shape)
    print("zz.shape",zz.shape);
    
    # 彩色可视化
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EE9A9A', '#FFF59D','#90CAF9'])
    # zz值不同，输出颜色不同
    plt.contourf(x0, x1, zz, cmap=custom_cmap)

# 根据可视化后的结果可以看出，原始数据normalization之后的数据，落在【-3，+3】之间
# 因此设置坐标值的范围如下：
xy = [-1.5, 2.5, -1.0, 1.5] 
plot_boundary(poly_svc, axis=xy)

plt.scatter(X[y==0,0], X[y==0,1], color = 'red')
plt.scatter(X[y==1,0], X[y==1,1], color = 'blue')
plt.show()

y_predict.shape (100000,)
zz.shape (250, 400)

（1）make_moons（）数据集

（2）make_circles（）数据集

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/123802467