密码学——公钥密码体系之ElGamal算法3

Posted 2022-03-03 摆渡沧桑

公钥密码体系之Elgamal算法3

1. ElGamal算法

ElGamal算法是基于离散对数求解困难的加密体系。与RSA算法一样，都能用于数据加密和数据签名。但是两者的原理不一样，ELGmal算法基于离散对数问题，而RSA算法基于大数分级困难问题。此外，对于ElGamal算法对于使用相同的私钥，对相同的明文进行加密，每次得到的加密结果却不一样，这是ElGamal算法另一个重要特征。

2. ElGamal算法基本原理

2.1 ElGamal密钥生成

1. 随机选择一个大素数$p$，且要求 $p-1$有大素数因子。再选择一个模$p$的本原元$g$。将$p$和$g$公开。
2. 随机选择一个整数$x$作为私钥，$2\le x\le p-2$
3. 计算$$y=g^{x}modp$$
   取$y$为公钥。

2.2 ElGamal加密过程

1. 对明文$M$进行加密，随机地选取一个整数$k$，$2\le k\le p-2$,并要求$k$与$p-1$互素
2. 计算：
   $$a＝g^{k}modp$$ $$b＝M\ast y^{k}modp$$
3. 密文对为$（a,b）$，并且密文的大小时明文的两倍。

2.3 ElGamal解密过程

1. 由密文可得明文$M$，计算
   $$M=b/a^{x}modp$$
   其中$x$为私钥。
2. 解密过程和Diffie-Hellman密钥交换过程极为类似。
3. 下面给出了加密和解密过程
   

2.4 ElGamal签名过程

签名：

1. 对消息$M$进行签名时，首先选择一个随机数$k$,并要求$k$与$p-1$互素。
2. 计算：
   $$a=g^{k}modp$$
3. 利用扩展欧几里得算法，求出$b$:
   $$M=(xa+kb)mod(p-1)$$
4. 签名结果为（a,b）。需要注意的是，k需要保密。

验签：

1. 需要验证下面公式成立：
   $$y^a{a}^{b}modp=g^{M}modp$$
2. 下面给出签名和验签的大致流程
   
3. 需要注意的是，在每次使用ElGamal算法进行签名时，都需要更新随机数k。

具体案例：

1. 选择$p=11,g=2$,私人秘钥$x=8$,计算：
   $$y=g^{x}modp=>y=2^{8}mod11=3$$
2. 因此，公开秘钥是$y=3,g=2,p=11$
3. 对消息$M=5$进行签名，首先随机选择随机数$k=9$，验证$gcd（9,10）=1$，计算：
   $$a=g^{k}modp=2^{9}mod11=6$$
   利用欧几里得算法求$b$:
   $$M=(ax+kbmod(p-1))$$ $$5=(8\ast 6+9\ast b)mod10$$
   求解得到$b=3$,于是签名对$(a,b)$为$（6,3）$
4. 验签上述签名的正确性，只需要验证下面：
   $$y^a{a}^{b}modp=g^{M}modp$$ $$3^6{6}^{3}mod11=2^{5}mod11$$

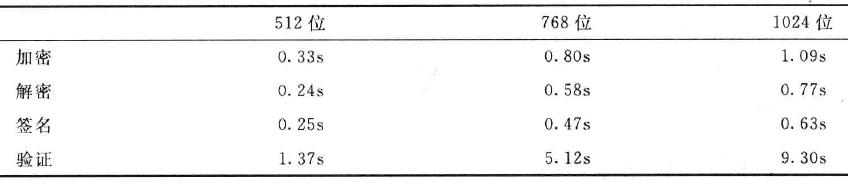
2.5 ElGamal算法软件算法实现的快慢

具有$160bit$的指数的ElGamal算法对不同模数长度的快慢表