算法模板-广度优先遍历

Posted 2022-02-27 周先森爱吃素

本文转载自Maple博客的算法模板-01背包问题，转载请注明出处。

简介

广度优先遍历（Breadth-First-Search，BFS），其特点便体现在广度，它是按“层“”来处理顶点，距离开始点最近的那些顶点首先被访问，而最远的那些顶点则最后被访问，这个和树的层序遍历很像。以下图为例：

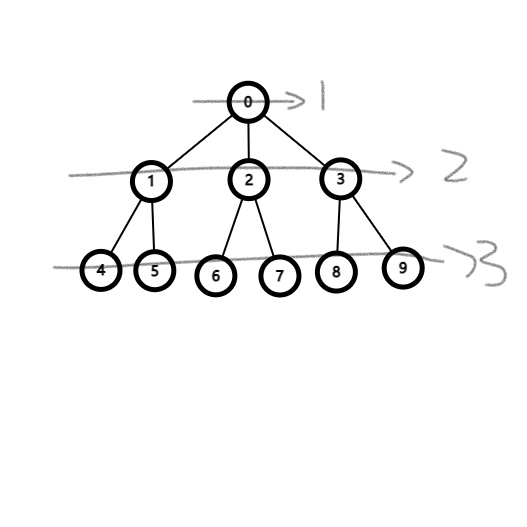
BFS尽可能地搜索与同一个节点连接的所有节点，再进行下一次搜索。

队列实现

显然，DFS一般都与由队列实现：

def BFS(node):
	q = collections.deque([root])
	while q:
		temp = q.popleft()
		print(temp.val)
		q.append(temp.nexts) # 所有与temp相连的节点均入队列

练习题1

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？
处。
示例1：

输入：m = 2, n = 3, k = 1
输出：3

示例2：

输入：m = 3, n = 1, k = 0
输出：1

这题需要判断机器人能走到的区域内的格子数量，代码如下：

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        q = collections.deque([(0, 0)])
        visited = set()
        count = 0
        while q:
            loc1, loc2 = q.popleft()           
            if loc1 < m and loc2 < n and (loc1, loc2) not in visited:
                visited.add((loc1, loc2))
                loc_k = sum([int(i) for i in str(loc1) + str(loc2)])
                if loc_k <= k:
                    count += 1
                    q.append((loc1 + 1, loc2))
                    q.append((loc1, loc2 + 1))
        return count

练习题2

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。
示例：

给定二叉树：
    3
   / \\
  9  20
    /  \\
   15   7
 输出为：
 [
  [3],
  [20,9],
  [15,7]
]

这题就是树的层序遍历，在遍历时顺便记录层数，奇数层和偶数层输出顺序不同，代码如下：

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        q, ans, flag = collections.deque(), [], 1
        q.append(root)
        while q:
            cur = collections.deque()
            while q:
                cur.append(q.popleft())
            ans_cur = []
            while cur:
                temp = cur.popleft()
                ans_cur.append(temp.val)
                if temp.left: q.append(temp.left)
                if temp.right: q.append(temp.right)
            ans.append(ans_cur if flag % 2 else ans_cur[::-1])
            flag += 1
        return ans

补充说明

面对“存在性检验”的搜索题，应当优先考虑基于递归的深度优先遍历和基于队列的广度优先遍历。