快速排序模板秦九昭算法模板深度优先搜索DFS广度优先搜索BFS图的遍历逆元中国剩余定理斯特林公式

Posted 2021-04-11 ACMfans Club

快速排序【模板】：

快速排序是基于二分思想、递归思想和分治思想而提出来的算法，排序的过程是：

1.选基准数（一般情况下选择第一个数即可）

2.把大于基准数的数放在基准数的右边，小于基准数的数放在基准数的左边（具体实现见代码）

3.快速排序实质上就是每一个基准数归位的过程

很有用的URL（漫画：什么是快速排序？（完整版））：http://www.sohu.com/a/246785807_684445

秦九昭算法【模板】

【tip】计算程序耗时工具

深度优先搜索（Depth First Search，DFS）

理解深度优先搜索的关键在于解决“当下该如何做”。至于“下一步如何做”则与“当下该如何做”是一样的。DFS的基本模型：

void dfs( int step )

{

    //判断边界

    //尝试每一种可能for(i=1;i<=n;i++)

    {

       //继续下一步dfs(dtep+1);

    }

    return ;

}

【例程1：走迷宫】

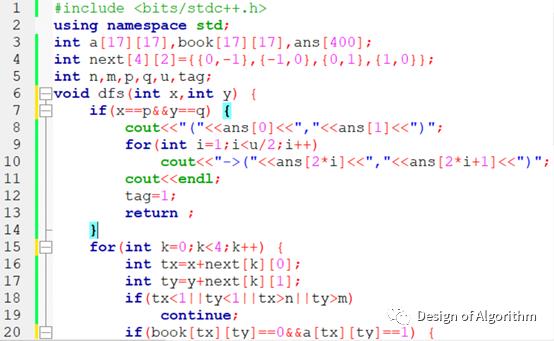
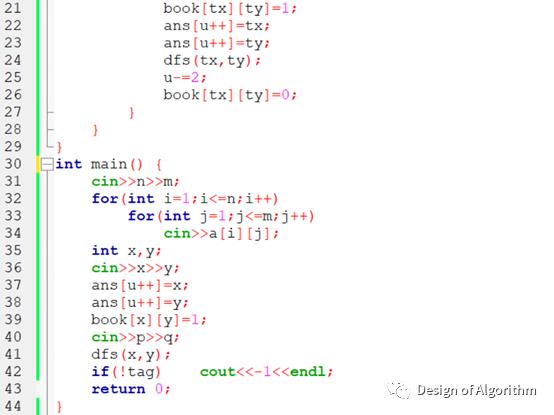
上面的dfs函数演示了深度优先搜索算法模型的一般结构，程序定义四个方向向量next二维数组，运用for循环遍历接下来四个有可能走到的坐标，如果坐标在迷宫之外，那么接着判断下一个坐标，直到结束位置；如果在迷宫之内，那么判断是否已经走过（book二维数组标记），是否存在路障，如果都没有，递归使用dfs进入下一步搜索（体现深度），为输出，定义ans数组来标记走过的每一个坐标，如果顺利到达迷宫出口，则把整个ans输出。

广度优先搜索（Breadth First Search，BFS）

BFS,就是从一个节点开始搜索,搜索完毕后,再从它四周的未访问过的节点开始搜索,重复之前的操作.它就像水波扩散一样.

【例程2：走迷宫改编(输出最短路径步数)】

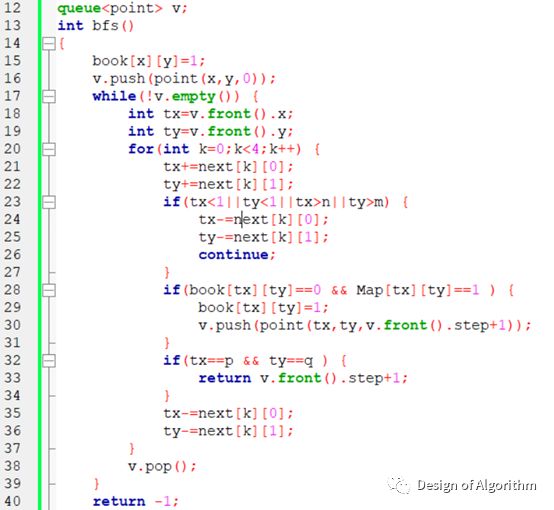
图的遍历

上面提到的BFS和DFS是基于图的遍历思想：

               深度优先遍历

首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；当没有未访问过的顶点时，则返回到上一顶点，继续试探访问别的顶点，直到所有顶点都被访问过。

无向图的邻接矩阵表示法深度遍历：

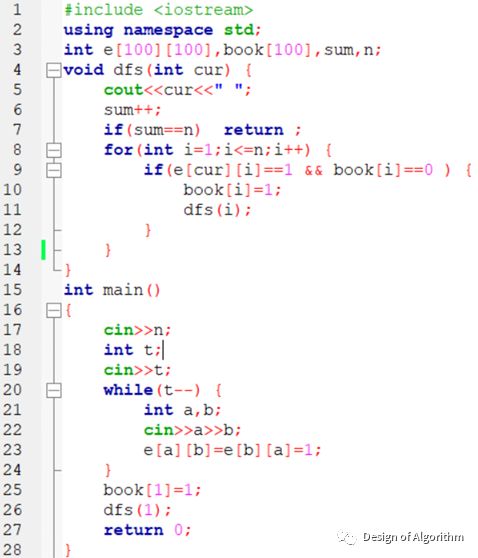
                广度优先遍历

广度优先遍历主要思想是：首先以一个未被访问过的顶点作为起始顶点，访问其所有相邻的顶点，然后对每个相邻的顶点，再访问他们相邻的未被访问过的顶点，直到所有顶点都被访问过。

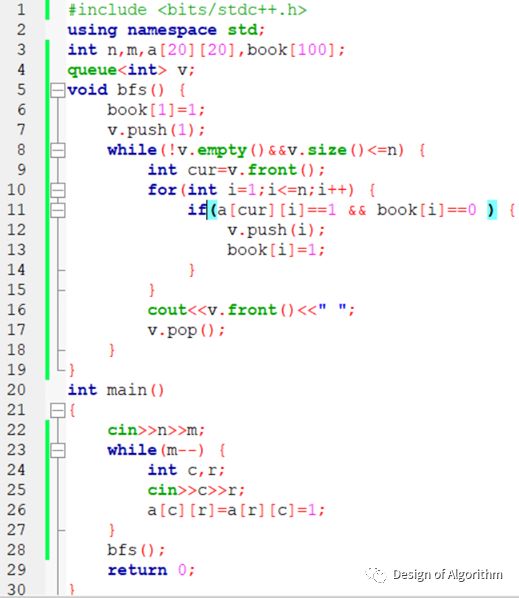
数论之 逆元

一般来说，存在：

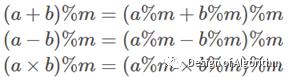
对于除法，取模的分配律不成立，需要用逆元将其转变为乘法，再使用分配律。若ab≡1 (mod m),则称a与b在模m的情况下互为逆元。记b=a⁻¹，所以b又叫a的数论倒数。

求逆元：

1.费马小定理：（只适用于模数为质数的情况）               

    根据逆元的定义，a mod p 的逆元就是a^p-2 ，于是：

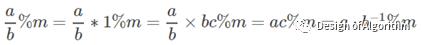
2.扩展欧几里得：

x×inv(x)≡1(modp) 其中 x,px,p 都是已知的。这就是一个未知数为 inv(x)inv(x) , 方程右侧的 c=1c=1 的同余方程 , 求 inv(x)inv(x) 的值, 解出此同余方程即可。

3.递推法：（只适用于模数为质数的情况，要解模的逆元的数 , 数量很多，但是连续）

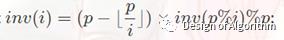
4.阶乘逆元法：（只适用于模数为质数的情况）

 

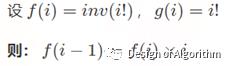
【例程3：乘法逆元模板】

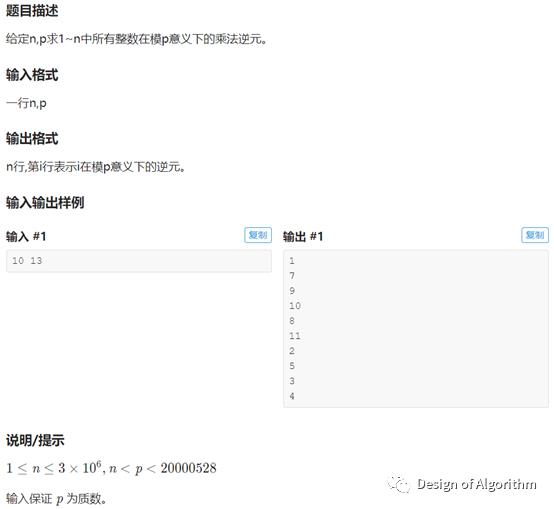
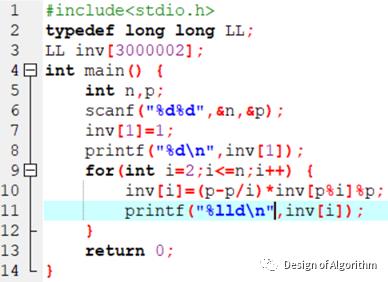
数论之 中国剩余定理初步(From Baidu pedia )

  同余定理：给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)。

  孙子定理是中国古代求解一次同余式组的方法。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

求解同余方程组：

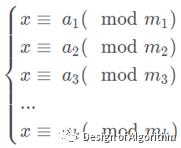
m₁~m_k两两互质，求最小解。

组合数学之 stirling公式

斯特林公式（Stirling's approximation）是一条用来取n的阶乘的近似值的数学公式。一般来说，当n很大的时候，n阶乘的计算量十分大，所以斯特林公式十分好用，而且，即使在n很小的时候，斯特林公式的取值已经十分准确。