剑指offer刷题动态规划（自用）

Posted 2022-02-05 王六六的IT日常

把数字翻译成字符串

题目描述：
给定一个数字，我们按照如下规则把它翻译为字符串：

0 翻译成 a，1 翻译成 b，……，11 翻译成 l，……，25 翻译成 z。

一个数字可能有多个翻译。

例如 $12258$ 有 $5$ 种不同的翻译，它们分别是 bccfi、bwfi、bczi、mcfi 和 mzi。

请编程实现一个函数用来计算一个数字有多少种不同的翻译方法。

参考力扣题解-lin-shen-shi-jian-lu-k 中的图：

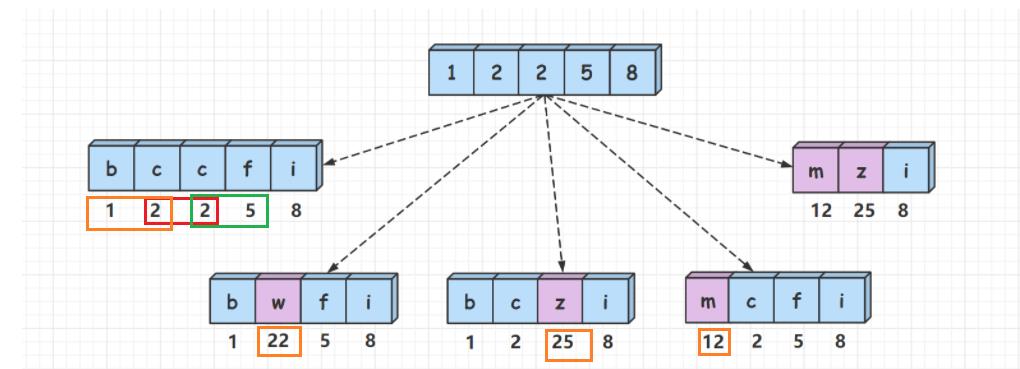
翻译规则：

• 将每一位单独翻译
• 将相邻两位组合起来翻译（组合数字范围在$10-25$之间）

为了可以很方便的将数字的相邻两位组合起来，我们可以先将数字num转化成字符串数组s[]。

状态表示：
定义f[i]表示前i个数字一共有多少种不同的翻译方法。
那么，f[n]就表示前n个数字一共有多少种不同的翻译方法，即为答案。

状态计算:
假设字符串数组为s[]，对于第i个数字，分成两种决策：

1. 单独翻译s[i]。由于求的是方案数，如果确定了第i个数字的翻译方式，那么翻译前i个数字和翻译前i - 1个数的方法数就是相同的，即f[i] = f[i - 1]。(s[]数组下标从1开始)
2. 将s[i]和s[i - 1]组合起来翻译(组合的数字范围在$10-25$之间)。如果确定了第i个数和第i - 1个数的翻译方式，那么翻译前i个数字和翻译前i - 2个数的翻译方法数就是相同的，即f[i] = f[i - 2]。(s[]数组下标从1开始)

最后将两种决策的方案数加起来，因此，状态转移方程为： f[i] = f[i - 1] + f[i - 2]。

K神题解

class Solution 
    public int translateNum(int num) 
        String s = String.valueOf(num);
        
        //字符数组
        char[] chs = s.toCharArray();
        int n = chs.length;
        
        //前i个字符有多少种翻译方法
        int[] dp = new int[n + 1]; 

        //翻译前0个数的方案数为1
        dp[0] = 1;
        dp[1] = 1;
        
        for(int i = 2;i <= n;i++)
            //单独翻译
            dp[i] = dp[i - 1];
            
            if(i > 1)
                int t = (chs[i - 2] - '0') * 10 + (chs[i - 1] - '0');
                //即两个组成的数字在[10,25]范围内才行。
                if(t >= 10 && t <=25 )
                    //将s[i] 和 s[i - 1]组合翻译
                    dp[i] += dp[i -2];
                

            
            
        
        return dp[n];

    

礼物的最大价值

题目描述：
在一个 $m\times n$ 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。
你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格直到到达棋盘的右下角。
给定一个棋盘及其上面的礼物，请计算你最多能拿到多少价值的礼物？

解题：

根据题目说明，易得某单元格只可能从上边单元格或左边单元格到达。

设$dp(i,j)$为从棋盘左上角走至单元格$(i,j)$的礼物最大累计价值，易得到以下递推关系：$dp(i,j)$等于$dp(i,j-1)$和$dp(i-1,j)$中的较大值加上当前单元格礼物价值$grid(i,j)$。

状态转移方程：
$$dp(i,j)=max[dp(i,j-1),dp(i-1,j)]+grid(i,j)$$

K神题解

class Solution 
    public int maxValue(int[][] grid) 
        int m = grid.length, n = grid[0].length;
        for(int i = 0; i < m; i++) 
            for(int j = 0; j < n; j++) 
                if(i == 0 && j == 0) 
                    continue;
                
                if(i == 0) 
                    grid[i][j] += grid[i][j - 1] ;
                else if(j == 0) 
                    grid[i][j] += grid[i - 1][j];
                else 
                    grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
                
            
        
        return grid[m - 1][n - 1];
    

当 grid矩阵很大时， i = 0或 j = 0的情况仅占极少数，相当循环每轮都冗余了一次判断。因此，可先初始化矩阵第一行和第一列，再开始遍历递推。
继续提高效率：

class Solution 
    public int maxValue(int[][] grid) 
        int m = grid.length, n = grid[0].length;
        
        // 初始化第一行 i= 0
        for(int j = 1; j < n; j++) 
            grid[0][j] += grid[0][j - 1];
        
            
        // 初始化第一列 j = 0
        for(int i = 1; i < m; i++) 
            grid[i][0] += grid[i - 1][0];
        
            
        for(int i = 1; i < m; i++)
            for(int j = 1; j < n; j++) 
                grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
               

              
        return grid[m - 1][n - 1];