剑指offer——第二十九天(动态规划“困难”）

Posted 2021-12-15 北聖

第二十九天——动态规划

• 第一题：剑指 Offer 19. 正则表达式匹配
• • • 问题描述
    • 思路
    • 代码
    • • 时间空间复杂度
    • 代码（皮一下）
    • • 时间空间复杂度
• 第二题：剑指 Offer 49. 丑数
• • • 问题描述
    • 思路
    • 代码
    • • 时间空间复杂度
• 第三题：剑指 Offer 60. n个骰子的点数
• • • 问题描述
    • 思路
    • 代码
    • • 时间空间复杂度

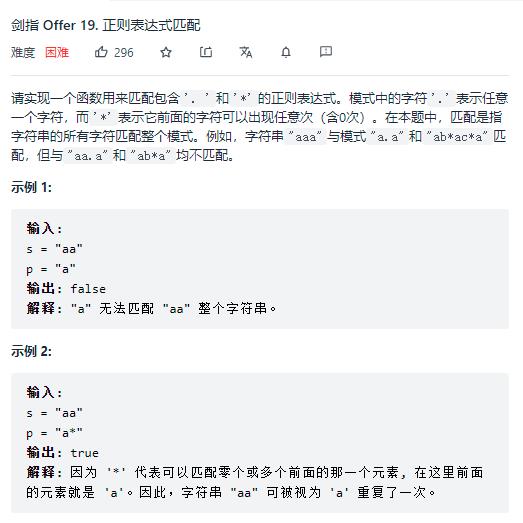
第一题：剑指 Offer 19. 正则表达式匹配

问题描述

思路

代码

public class Solution 

    // 最直观版
    public boolean isMatch(String s, String p) 
        int m = s.length();
        int n = p.length();
        // dp[i][j]表示s前i-1个字符,p前j-1个字符是否匹配
        boolean[][] dp = new boolean[m + 1][n + 1];
        // dp[0][0] :s前0个字符和p的前0个字符默认是空串=匹配
        // 注意：由于多了[0][0],所以dp[i][j],定位到的是s[i-1]和p[j-1]的字符
        dp[0][0] = true;
        // 初始化首行:当s为空串,p的偶数位为*才能匹配
        for (int j = 2; j < n + 1; j += 2) 
            dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
        
        // 状态转移
        for (int i = 1; i < m + 1; i++) 
            for (int j = 1; j < n + 1; j++) 
                // 当p[j-1]=*时,有三种情况
                if (p.charAt(j - 1) == '*') 
                    if (dp[i][j - 2]) // p[j-2]出现0次,i和j指向字符的长度均相同
                        dp[i][j] = true;
                     else if (dp[i - 1][j] && s.charAt(i - 1) == p.charAt(j - 2)) // p[j-2]出现1次 且 当前i-1和j-2指向的字符相同
                        dp[i][j] = true;
                     else if (dp[i - 1][j] && p.charAt(j - 2) == '.') // 最特殊情况:p[j-2]=. p[j-1]=*时 是万能匹配
                        dp[i][j] = true;
                    
                 else // 当p[j-1]!=*时,有两种情况
                    if (dp[i - 1][j - 1] && s.charAt(i - 1) == p.charAt(j - 1)) // 前面元素之前都匹配 且 当前元素也相容
                        dp[i][j] = true;
                     else if (dp[i - 1][j - 1] && p.charAt(j - 1) == '.')  //  前面元素之前都匹配 且 p的当期元素是.
                        dp[i][j] = true;
                    
                
            
        
        return dp[m][n];
    

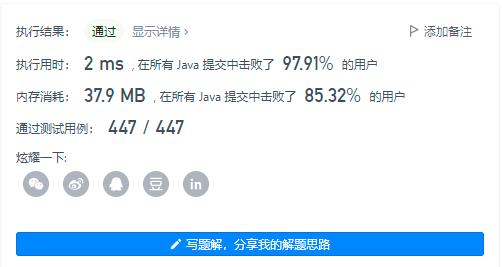
时间空间复杂度

代码（皮一下）

class Solution 
    public boolean isMatch(String s, String p) 
        return s.matches(p);
    

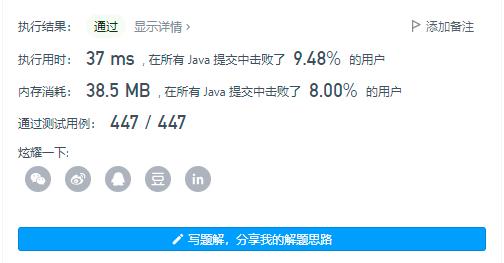
时间空间复杂度

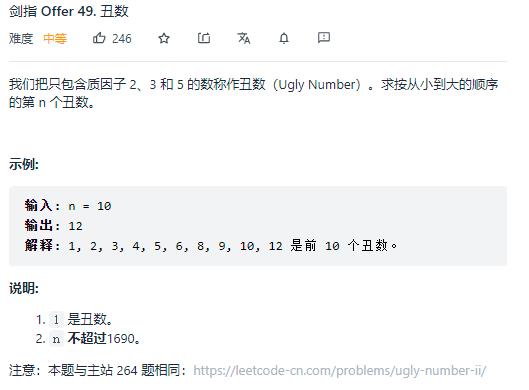
第二题：剑指 Offer 49. 丑数

问题描述

思路

代码

class Solution 
    public int nthUglyNumber(int n) 
        if(n <= 0) return -1;
        int [] dp = new int [n];
        dp[0] = 1;
        int id2 = 0,id3 = 0, id5 = 0;
        for(int i=1;i < n;i++)
            dp[i] = Math.min(dp[id2] * 2,Math.min(dp[id3] * 3,dp[id5]*5));
            if(dp[id2]*2 == dp[i]) id2 += 1;
            if(dp[id3]*3 == dp[i]) id3 +=1;
            if(dp[id5]*5 == dp[i]) id5 += 1;
        
        return dp[n -1];
    

时间空间复杂度

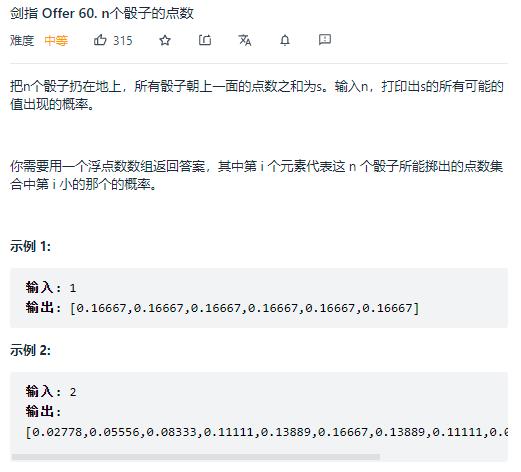
第三题：剑指 Offer 60. n个骰子的点数

问题描述

思路

代码

class Solution 
    public double[] dicesProbability(int n) 
        double[] dp = new double[6];
        Arrays.fill(dp, 1.0 / 6.0);
        for (int i = 2; i <= n; i++) 
            double[] tmp = new double[5 * i + 1];
            for (int j = 0; j < dp.length; j++) 
                for (int k = 0; k < 6; k++) 
                    tmp[j + k] += dp[j] / 6.0;
                
            
            dp = tmp;
        
        return dp;
    

时间空间复杂度