LaTeX入门——如何独立排版出一篇期刊论文
Posted 统计学小王子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LaTeX入门——如何独立排版出一篇期刊论文相关的知识,希望对你有一定的参考价值。
LaTeX入门目录
0引言
0.1本文工作
因为平时使用LaTeX较少,本身对LaTeX不是很熟悉,所以文本不会系统且全面的介绍如何使用LaTeX制作一些精美的PPT、简历、报告、科技文章,也不会从头到尾教大家建议一套可用的LaTeX模板。但是本文想尽力解决在拿到模板后如何独立排版出一篇科技论文这一问题。从LaTeX软件的安装到期刊模板的使用,再到一些基本的配套插件,并分享一些主要的统计相关的使用技巧.
排版一篇文论需要一下几个方面的考虑:
– LaTeX软件的安装
– 公式的制作与引用
– 图的插入
– 表的制作与插入
– 参考文献的制作与引用
– 其他常用的方面
0.2 为什么学习LaTeX???(LaTeX VS Word)
在使用LaTeX之前大多数人使用的应该是Word来排版自己需要的报告、文档、待发表的文章甚至是书籍。相比较本文的LaTeX而言,Word给人的感觉是可见即可得,交互性比较好,而且排版功能还是比较强大的,但是我们为什么还需要付出学成本学习LaTeX呢。下面客观总结一下LaTeX的优缺点:
LaTeX优点
– 对于科研人员来说很多编辑设会提供或者只提供LaTeX模板给作者。
– 合适的使用模板会让你的文章or书籍快速接近印刷级别的水平。
– 更加便捷的排版大量的数学公式。
– 学习程高本相对不高(相对R语言、py等语言)。通过使用固定的模板和学习少量的命令可以快速的生成自己需要的文档。
– 相对于R的扩展包而言,LaTeX也具有很多功能强大的扩展红宏使用,用以实现大多数人的排版需求。
– 使用平台广泛:常见PC系统(XP win 7 -10 mac)都有相应的LaTeX版本与之对应。
当然我使用的比较少,除了上述优点外还有很多其他的有点等待着你们去发现。下面聊一下我感受到的缺点。
LaTeX缺点
– 自己从头设计版面,还是需要一定的学习成本和时间的付出。
– LaTeX更加擅长一下诸如文章书籍PPT等有结构化模板的排版任务,一些非结构化的排版任务就不是很方便使用LaTeX来做。
– 想熟练掌握LaTeX的大部分命令还是需要一定时间和练习。
– 不能可见即可得,想要预览需要LaTeX编译一下才可以。
总结
各种不同的软件都有自己的适用场景,在不强制的情况下大家可以自己选择自己熟练和适合自己的软件即可。
1、软件的安装
latex排版软件我知道两个:Ctex套装和texlive两个,这两个软件可以同时安装。如果要下载可以下载ctex套装,理由如下:Ctex套装安装简单,不需要配置外置编译器和pdf生成器,对电脑的配置要求相对texlive较低。排版编程界面比较友好,适应绝大多数的模板,已安装好大部分常用包。当然有条件也可以同时安装texlive,因为也确实有模板在Ctex套装不可以兼容,由于编译洁面和功能比较简陋,这时候需要自己配置编译器,推荐两个周围人常用和我自己在用的编译器:WinEdt 10、texstudio、SumatraPDF.下面提供了下载网址点击链接即可,有需要自己移步去看,这里就不重复列出了。链接。
也可以自定百度(这里用的是必应)。
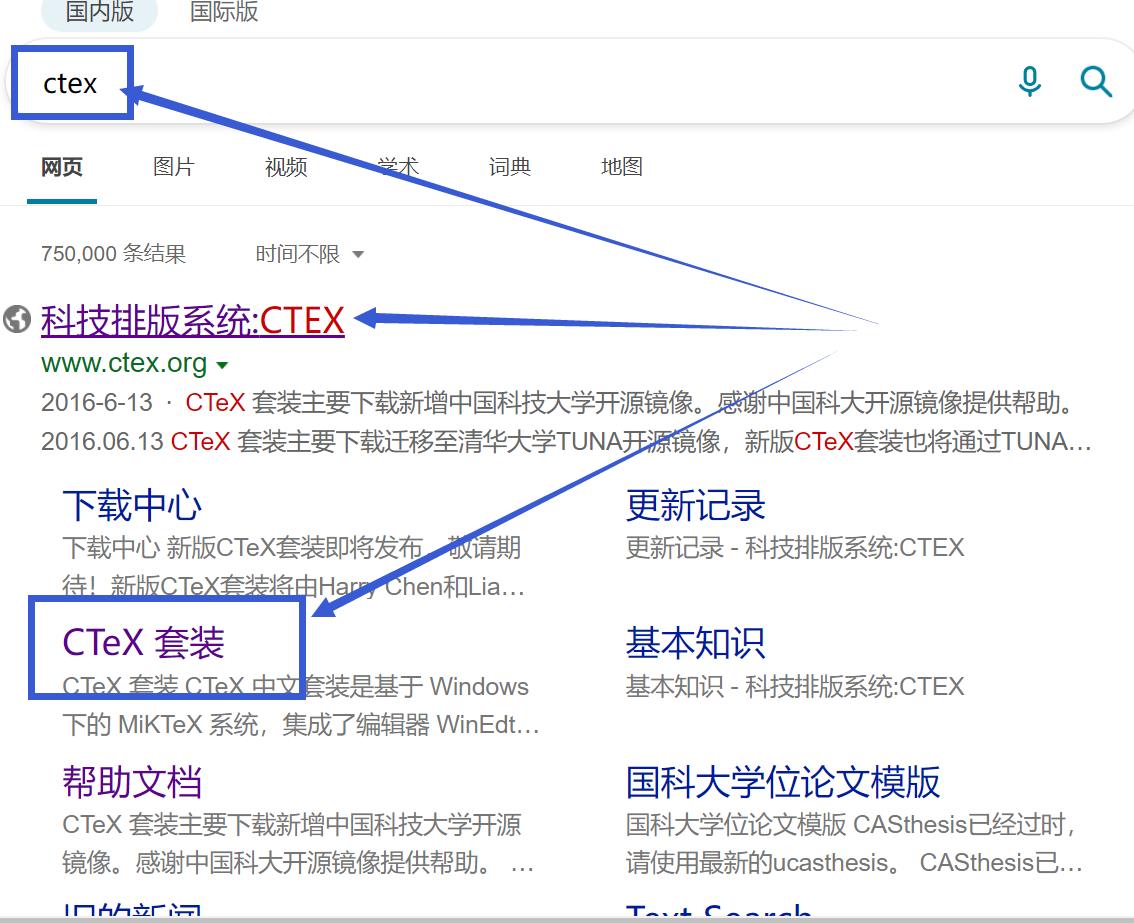
1.1 Ctex下载地址
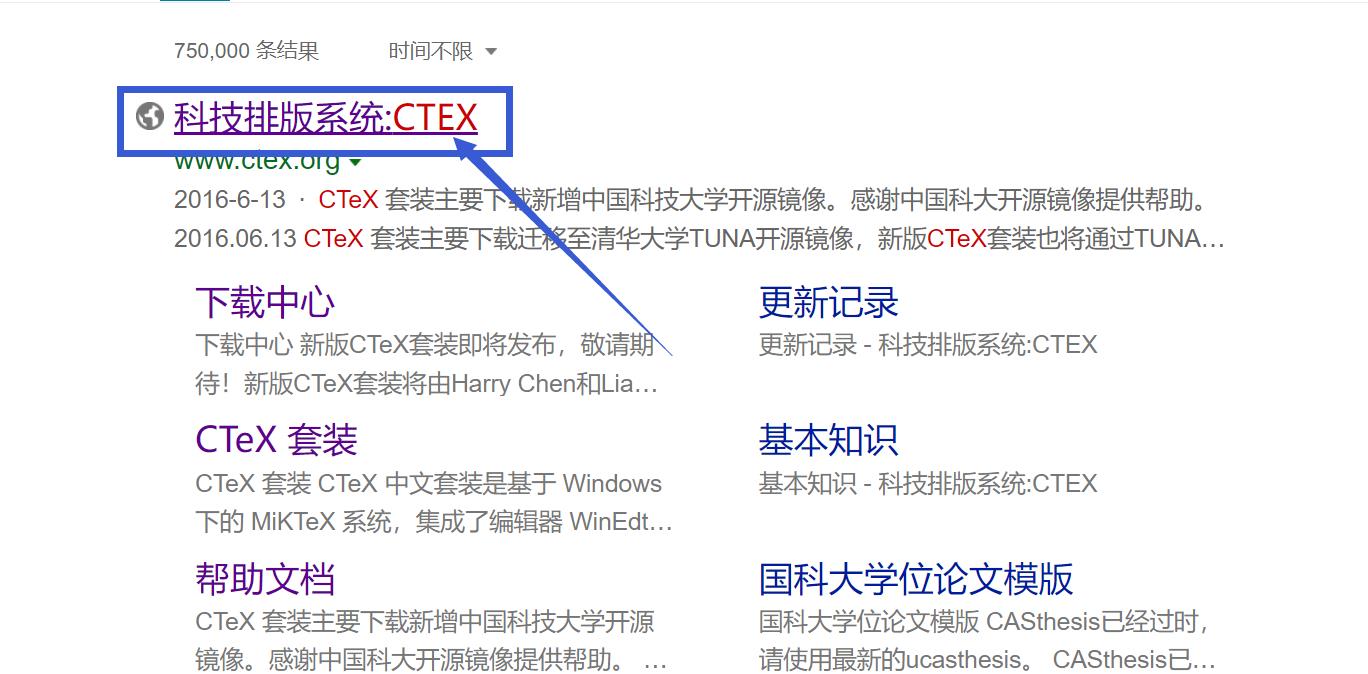


最后找一个自己喜欢得方式下载安装即可。
1.2 texlive的下载地址
引言中的链接其实已经给了下载地址,可以自己按需求去下载,不过这个安装会有点麻烦,如果遇到问题可以自行百度安装。
2、公式制作与引用
在介绍公式之前说明一下LaTeX文档的基本结构。
\\documentclass[a4paper,12pt]article %% 设置文档类别,12pt字体和A4纸
\\usepackage[12345678]-------- %%载入宏包
\\begindocument %% 文档开始
正文书写内容
\\enddocument %% 文档结束
上面是一下常见的LaTeX格式,一般都是在正文内容编辑。
2.1 公式几种形式
形式一:单$
前文,$x + y = 2$,后文
结果一:
前文,
x
+
y
=
2
x + y = 2
x+y=2,后文
形式二:双$
$$x + y = 2$$
结果二:
x
+
y
=
2
x + y = 2
x+y=2
形式三:\\beginalign ***\\endalign
\\beginalign
x + y = 2
\\endalign
结果三:
x
+
y
=
2
(1.1)
x + y = 2\\tag1.1
x+y=2(1.1)
形式四:\\beginequation ***\\endequation
\\beginequation
x + y = 2
\\endequation
结果四:
x
+
y
=
2
(1.2)
x + y = 2\\tag1.2
x+y=2(1.2)
形式五:\\[ ***\\]
\\[x + y = 2\\]
结果五:
x
+
y
=
2
x + y = 2
x+y=2
总结:以上五种排版生成方式都可以用来生成公式,其中单$是句内部排版公式,其他四种方式是用来句间排版公式,一般是公式居中显示。\\beginalign ***\\endalign和\\beginequation***\\endequation可以对公式自动编号。下面以\\beginequation***\\endequation为例子进行进行其他公式的说明。
2.2公式的编号与引用
2.2.1自动编号+自动引用
代码一:
注意:要想引用公式需要使用\\label给公式起名字。才可以使用名字进行自动引用
\\beginequation
x + y = 1 \\labeleq1
\\endequation
\\beginequation
x + y = 2 \\labeleq2
\\endequation
公式\\refeq1和公式\\refeq2的引用。
效果一:
x
+
y
=
1
(1.3)
x + y = 1 \\tag1.3
x+y=1(1.3)
x
+
y
=
2
(1.4)
x + y = 2 \\tag1.4
x+y=2(1.4)
公式1.3和公式1.4的引用。
代码二:
也可以通过\\notag命令去掉自动编号的命令。
\\beginequation
x + y = 2 \\notag
\\endequation
效果二:
x
+
y
=
2
x + y = 2
x+y=2
2.2.2手动编号+手动引用
代码一:
\\beginequation
x + y = 3 \\tag1.1.1
\\endequation
\\beginequation
x + y = 3 \\tag2.5.6
\\endequation
公式(1.1.1)和公式(2.5.6)的引用。
效果一:
x
+
y
=
1
(1.1.1)
x + y = 1 \\tag1.1.1
x+y=1(1.1.1)
x
+
y
=
2
(2.5.6)
x + y = 2 \\tag2.5.6
x+y=2(2.5.6)
公式(1.1.1)和公式(2.5.6)的引用。
2.2.3子公式的编号和引用
代码一:
子公式自动编号:
\\beginalign
x + y = k \\labeleq3\\\\
x + y = k \\notag \\\\
x + y = k \\labeleq4
\\endalign
\\beginsubequations
\\beginalign
x + y = k \\labeleq5\\\\
x + y = k \\notag \\\\
x + y = k \\labeleq6
\\endalign
\\endsubequations
\\par 公式\\refeq3、公式\\refeq4、公式\\refeq5和公式\\refeq6的引用。
效果一:
x
+
y
=
k
(1.5)
x
+
y
=
k
x
+
y
=
k
(1.6)
\\beginaligned & x + y = k \\text (1.5)\\\\ &x + y = k\\\\ &x + y = k \\text (1.6) \\endaligned
x+y=k (1.5)x+y=kx+y=k (1.6)
x
+
y
=
k
(1.7a)
x
+
y
=
k
x
+
y
=
k
(1.7b)
\\beginaligned & x + y = k \\text (1.7a)\\\\ &x + y = k\\\\ &x + y = k \\text (1.7b) \\endaligned
x+y=k (1.7a)x+y=kx+y=k (1.7b)
公式1.5、公式1.6、公式1.7a和公式1.7b的引用。类似的也可以通过\\tag手动编号和绝对引用。
2.3 公式与R语言的交互
上面介绍了在LaTeX中常用的创建公式的方式,以及如何对公式进行打标签,编号和引用。其实平时绘图和编辑Markdown命令的时候也会使用到类似的LaTeX公式,我一般使用的比较多的Markdown是CSDN中的博客编译器以及RMarkdown。R语言是以统计计算和统计可视化见长的统计软件,这部分以R语言中的应用为例子认识一下LeTeX基本公式语法。
往图中添加标签公式的方法有很多,R基础包自带的expression函数就是一个,除此之外还有latex2exp可以在R语言中使用latex的命令来给图片添加公式。《R语言画图之——expression》1基于expression函数常用的命令从常用的运算符、大型运算、集合运算、希腊字母等方面给出常用的公式命令。而latex2exp包则使用TeX函数实现LaTeX公式的创建,以上两种方式都可以在基础绘图和ggplot2等R语言的绘图系统中使用。
下面给出R语言的代码和例子:
plot(0, 0, xlim = c(5,6), ylim = c(5,6),
xlab = expression(beta),
ylab = expression(gamma))
text(5.5, 5.5, expression(frac(1, beta)), cex = 2)
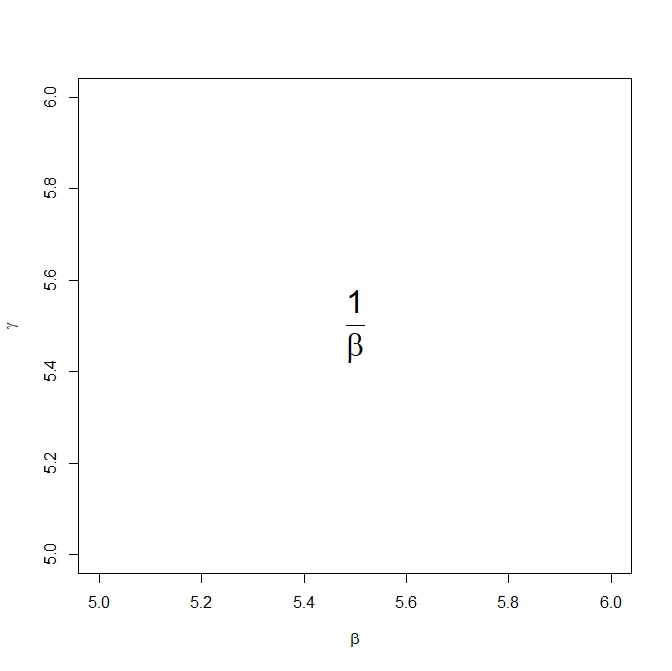
2.4常用公式汇总
数学公式是非常多的,在《LaTeX公式手册(全网最全)》2中整理了大部分的我们有可能会用到的公式,下面是这篇博客的目录,有兴趣的同学可以自己移步去浏览查看。想要全部记住是需要一定的时间和精力,本小节给出平时用的多一些的公式和数学符号。

2.4.1 初等函数和基本运算
$$
\\hat\\beta,
a^b,
\\log_10 x,
\\log e,
\\sin a,
\\arcsin a,
\\min(x1,x2),
\\max(x1,x2),
\\lim_x \\to +\\infty \\frac1x(x+1),
g', g'', g^(3),
\\sqrt2,
\\boxplus,
\\oplus,
\\circleddash,
\\bigoplus
$$
β ^ , a b , log 10 x , log e , sin a , arcsin a , min ( x 1 , x 2 ) , max ( x 1 , x 2 ) , lim x → + ∞ 1 x ( x + 1 ) , g ′ , g ′ ′ , g ( 3 ) , 2 , ⊞ , ⊕ , ⊝ , ⨁ \\hat\\beta, a^b, \\log_10 x, \\log e, \\sin a, \\arcsin a, \\min(x1,x2), \\max(x1,x2), \\lim_x \\to +\\infty \\frac1x(x+1), g', g'', g^(3), \\sqrt2, \\boxplus, \\oplus, \\circleddash, \\bigoplus β^,ab,log10x,loge,sina,arcsina,min(x1,x2),max(x1,x2),x→+∞limx(x+1)1,g′,g′′,g(3),2,⊞,⊕,⊝,⨁
2.4.2集合逻辑符号
$$
\\varnothing,
\\in,
\\notin ,
\\subset,
\\subseteq,
=,
\\ne,
\\neq,
\\approx,
<,\\le,
\\ge,
\\leqslant,
\\geqslant,
\\exists,
\\therefore,
\\because,
\\cap,
\\cup
$$
∅ , ∈ , ∉ , ⊂ , ⊆ , = , ≠ , ≠ , ≈ , < , ≤ , ≥ , ⩽ , ⩾ , ∃ , ∴ , ∵ , ∩ , ∪ \\varnothing, \\in, \\notin ,\\subset,\\subseteq,=, \\ne, \\neq,\\approx,<,\\le,\\ge,\\leqslant,\\geqslant, \\exists,\\therefore, \\because,\\cap,\\cup ∅,∈,∈/,⊂,以上是关于LaTeX入门——如何独立排版出一篇期刊论文的主要内容,如果未能解决你的问题,请参考以下文章