R语言入门--第十一节（置换检验与自助法求置信区间）

Posted 2023-05-04

参考技术A 原理参考 文章 ，主要思想我认为是求出所有分布的可能（中间的一般为零假设），出现这种分布的概率。

distribution= 参数可为exact（精确模式，即依据所有可能的排列组合，仅适用于两样本问题）、approxiamate(nresample=#)（蒙特卡洛抽样，#指需要重复的次数）、asymptotic（渐进分布抽样）

lmPerm包更擅长方差分析。示例实验设计仍为5组接受不同治疗方法的多组结果比较。

实验示例仍为关节炎的治疗（两种）与效果（无、部分、显著）间的关系

实验示例为研究文盲率与谋杀率是否相关

主要为 lmp() 、 aovp() 两个函数分别对应参数法的 lm() 线性回归、 aov() 方差分析。主要格式上的区别是添加了 perm= 参数。可以为Exact（精确模式）、Prob（不断从可能的序列中抽样，直至估计的标准差在估计的p值0.1之下）、SPR（使用贯序概率比检验来判断何时停止抽样）。值得注意的是当样本观测大于10，perm="Exact"自动默认转为"Prob"，因此精确检验只适用于小样本问题。

（1）简单线性回归
实验示例仍为以身高预测体重的设计

（2）多项式回归
高精度拟合身高体重回归关系

（3）多元回归
探究谋杀率与多因素的回归关系

（1）单因素方差分析

（2）单因素协方差分析
实验示例仍为药物对刚出生小鼠体重影响，协变量为怀孕时间

（3）双因素方差分析（交互效应）
实验示例：两种药物分别在不同剂量下对小鼠牙齿长度的影响。

核心思想是有放回的抽样多次（1000次）

（1）写一个能返回带研究统计量的函数；
（2）确定重复数，使用 boot() 函数处理；（一般重复1000次即可；此外有人认为初始样本大小为20-30即可得到足够好的结果）；
（3） boot.ci() 函数计算统计量置信区间。

实验示例：使用mtcar数据框，采用多元回归，根据车重和发动机排量来预测汽车的每加仑行驶的英里数。想获得95%的R平方值（预测变量对响应变量可解释的方差比）的置信区间
（1）首先写函数

（2）然后使用boot()函数

（3）最后boot.ci()函数求置信区间

实验示例：使用mtcar数据框，采用多元回归，根据车总和发动机排量来预测汽车的每加仑行驶的英里数。想获取一个统计量向量--三个回归系数（截距项、车总、发动机排量）95%的置信区间。

R语言Wald检验 vs 似然比检验

 原文链接：http://tecdat.cn/?p=6895

在开展基于概率推理的课程时，关键主题之一是基于似然函数的检验和置信区间构建。通常包括Wald，似然比和分数检验。在这篇文章中，我将修改Wald和似然比检验的优缺点。我将重点关注置信区间而不是检验 。

示例

我们将X表示观察到的成功次数的随机变量，x表示其实现的值。似然函数只是二项式概率函数，但参数是模型参数。 所以MLE只是观察到的比例。

Wald置信区间 

如果我们使用将参数空间（在我们的示例中为区间（0,1））映射到整个实线的变换，那么我们保证在原始比例上获得仅包括允许参数值的置信区间。

 

对于概率参数绘制的n = 10，x = 1的二项式示例的对数似然函数：

从视觉上我们可以看出，对数似然函数在绘制时 实际上不是二次方。下图显示了相同的对数似然函数，但现在x轴是对数几率：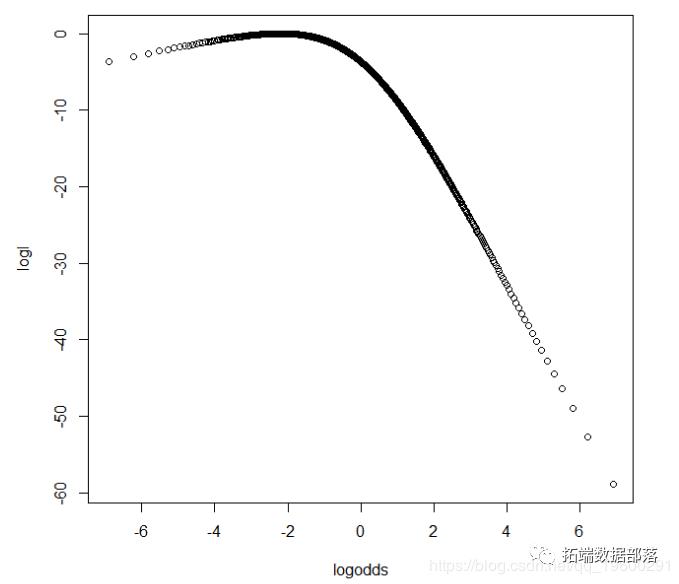

二项式的对数似然函数n = 10 x = 1检验，相对于对数几率。

 

似然比置信区间

虽然似然比方法具有明显的统计优势，但计算上Wald区间/测试更容易。在实践中，如果样本量不是太小，并且Wald间隔是以适当的比例构建的，它们通常是合理的。然而，在小样本中，似然比方法可能是优选的。

点击标题查阅往期内容

更多内容，请点击左下角“阅读原文”查看

案例精选、技术干货 第一时间与您分享

长按二维码加关注

更多内容，请点击左下角“阅读原文”查看