7.激励函数(激活函数)

Posted 2023-04-28

参考技术A 在计算机深度学习时，总会经常遇到一些之前完全没有听说过的词汇，比如 激励函数、卷积、池化、交叉熵 ，刚开始可能会觉得特别生涩、一时间不理解，这没关系，当深入理解这个词汇背后所代表的具体含义后，发现其实这些词汇也是可以慢慢接受的(习惯了就好了...)。

通常，一层中的神经元经过加权求和，然后再经过非线性方程得到的结果转化为输出，或者作为下一层的输入。激励函数，说白了就是非线性方程。

激励函数的作用：通过激活函数会将数据压缩到一定的范围区间内，得到的数据的大小将决定该神经元是否处于活跃状态，即：是否被激活。这使得神经网络可以更好地解决较为复杂的问题。

常见的激励函数：sigmoid函数、tanh函数、ReLu函数、SoftMax函数等等。

先来看下sigmoid函数表达式：

sigmoid函数图像：

优点：
1.输出结果在(0, 1)之间，输出范围有限，优化起来稳定可控；
2.单调连续，求导方便；

缺点：
1.根据图像也可容易看出：极易饱和。
当输入范围在(-∞, -4)或(4, +∞)时，就落入了饱和区，一阶导数接近0，这就使得容易产生梯度消失，进而导致训练出现问题。

2.输出是在(0, 1)之间，这是优点；但不是以0为中心，所以也是缺点。

tanh函数表达式及图像：

优点：
1.输出结果在(-1, 1)之间，输出范围有限，且以0为中心；
2.单调连续，收敛速度比sigmoid更快；

缺点：
1.根据图像也可容易看出：同sigmoid一样，极易饱和。
当输入范围在(-∞, -2)或(2, +∞)时，就落入了饱和区，一阶导数接近0，这就使得容易产生梯度消失，进而导致训练出现问题。

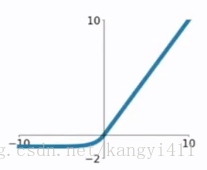
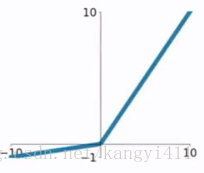
ReLu函数表达： f(x) = max(0, x)
ReLu函数图像：

优点：
1.收敛速度比sigmoid、tanh函数更快；
2.当x>0时，保持梯度不衰减，从而可以有效缓解梯度消失的问题。

缺点：
1.当x<0时，硬饱和，这会导致部分输入对应的权重无法更新，可能会出现“神经元死亡”。

softplus 函数对 relu函数 做了平滑处理，其表达式为： f(x) = log(1 + e^x) ;

我们先来看看这种激励函数出现的输出层是什么样子:

从样子上来看这种方式跟普通的全连接层没有什么区别，但是激励函数的形式却大大 不同 。
首先后面一层作为预测分类的输出节点，每一个节点就代表一个分类 ，那么这 7个节 点就最多能够表示 2 个分类的模型 。 任何一个节点的激励函数都是：

其中 i就是节点的下标次序，而：

也就是说这是一个线性分类模型的输出作为自然常数e的指数。 最有趣的是最后这一层有这样一个特性，那就是:

也就是说最后一层的每个节点的输出值加和是1。 这种激励函数从物理意义上可以解释为一 个样本通过网络进行分类的时候在每个节点上输出的值都是小于等于1的，是它从属于这个分类的概率。

在训练的时候方法大家可能也已经猜到了，就是拿到一个训练样本和给分 类标签一个下标序号，然后对应的节点给1，其他给0。

说明：SoftMax这种激励函数使用的损失函数看上去比较特殊，叫做交叉熵 (cross entropy) 损失函数。 什么叫交叉摘损失函数呢，如何理解这种函数呢? 等后面总结代价函数时专门介绍。

当一个神经元以概率 keep_prob 为标准决定是否被激活，如果被激活，那么该神经元的输出将被放大到原来的 1/keep_prob 倍；如果不被激活，则神经元的输出为0。

默认情况下，每个神经元是否被激活是相互独立的。dropout激活函数格式为：
tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None, name=None)

激励函数在神经网络中起着非常重要的作用，理论上添加激励函数的神经网络可以收敛为任意一个函数，因激励函数各有特色，所以使用时，应根据具体情况具体分析。一般选用规则为：

-当输入的数据特征相差明显时，用tanh效果更好；
-当特征相差不明显时，用sigmoid函数比较好；
-sigmoid和tanh作为激励函数需要对输入进行规范化处理，否则激活后的值可能进入饱和区，而relu不会出现这种情况，有时relu甚至不需要要求输入规范化，因此目前85%～90%的神经网络会采用relu函数。

tf.sigmoid(features, name=None)

tf.tanh(features, name=None)

tf.nn.relu(features, name=None)

tf.nn.softplus(features, name=None)

tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None, name=None)

对神经网络学习中的激励函数进行总结。激励函数，说白了就是非线性方程。

机器学习之激励函数

1、sigmoid

函数曲线如下:

sigmoid激活函数，符合实际，当输入值很小时，输出接近于0；当输入值很大时，输出值接近于1。

sigmod函数曾经是比较流行的，它可以想象成一个神经元的放电率，在中间斜率比较大的地方是神经元的敏感区，在两边斜率很平缓的地方是神经元的抑制区。当然，流行也是曾经流行，这说明函数本身是有一定的缺陷的：

1) 当输入稍微远离了坐标原点，函数的梯度就变得很小了，几乎为零。在神经网络反向传播的过程中，我们都是通过微分的链式法则来计算各个权重w的微分的。当反向传播经过了sigmod函数，这个链条上的微分就很小很小了，况且还可能经过很多个sigmod函数，最后会导致权重w对损失函数几乎没影响，这样不利于权重的优化，这个问题叫做梯度饱和，也可以叫梯度弥散。

2) 函数输出不是以0为中心的，这样会使权重更新效率降低。对于这个缺陷，在斯坦福的课程里面有详细的解释。

3) sigmod函数要进行指数运算，这个对于计算机来说是比较慢的。

2、tanh

tanh函数曲线如下：

tanh函数和sigmod函数的曲线是比较相近的。

首先相同的是，这两个函数在输入很大或是很小的时候，输出都几乎平滑，梯度很小，不利于权重更新；不同的是输出区间，tanh的输出区间是在(-1,1)之间，而且整个函数是以0为中心的，这个特点比sigmod的好。

一般二分类问题中，隐藏层用tanh函数，输出层用sigmod函数。不过这些也都不是一成不变的，具体使用什么激活函数，还是要根据具体的问题来具体分析，还是要靠调试的。

3、Relu

Relu修正线性单元是有许多优点，是目前神经网络中使用最多的激活函数。

函数曲线如下：

优点：（1）在输入为正数的时候，不存在梯度饱和问题。不会出现梯度消失，收敛速度快；

           （2）前向计算量小，只需要计算max(0, x)，不像sigmoid中有指数计算；

           （3）反向传播计算快，导数计算简单，无需指数、出发计算；           

           （4）有些神经元的值为0，使网络具有saprse（稀疏的; 稀少的）性质，可减小过拟合。

 

缺点：

　　    （1）当输入是负数的时候，ReLU是完全不被激活的，这就表明一旦输入到了负数，ReLU就会死掉。这样在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，后面的参数就会不更新（使用合适的学习率会减弱这种情况）这个和sigmod函数、tanh函数有一样的问题。

           （2） 我们发现ReLU函数的输出要么是0，要么是正数，这也就是说，ReLU函数也不是以0为中心的函数。

 

4.ELU函数

 

ELU函数公式和曲线如下图

 

 

 

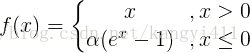
ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

5.PReLU函数

PReLU函数公式和曲线如下图

 

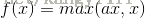
PReLU也是针对ReLU的一个改进型，在负数区域内，PReLU有一个很小的斜率，这样也可以避免ReLU死掉的问题。相比于ELU，PReLU在负数区域内是线性运算，斜率虽然小，但是不会趋于0，这算是一定的优势吧。我们看PReLU的公式，里面的参数α一般是取0~1之间的数，而且一般还是比较小的，如零点零几。当α=0.01时，我们叫PReLU为Leaky ReLU，算是PReLU的一种特殊情况吧。

总体来看，这些激活函数都有自己的优点和缺点，没有一条说法表明哪些就是不行，哪些激活函数就是好的，所有的好坏都要自己去实验中得到。