如何用matlab解多元非线性方程组

Posted 2023-04-24

使用solve函数。

举个例子，解非线性方程组 x^2+y^3=10 x^3-y^2=1 其中x,y为方程组的未知量 在Matlab的命名窗口中输入： 

syms x y  [x y]=solve('x^2+y=10','x^2-y^2=1','x','y')  即可  输出计算结果为： 

x =       (37^(1/2)/2 + 21/2)^(1/2)     (21/2 - 37^(1/2)/2)^(1/2)  -(21/2 - 1/2*37^(1/2))^(1/2)  -(1/2*37^(1/2) + 21/2)^(1/2)   

y =    - 37^(1/2)/2 - 1/2    37^(1/2)/2 - 1/2    37^(1/2)/2 - 1/2  - 37^(1/2)/2 - 1/2 

具体solve函数的使用方法，通过输入help solve来学习。

20世纪60年代中期以后，发展了两种求解非线性方程组(1)的新方法。

一种称为区间迭代法或称区间牛顿法，它用区间变量代替点变量进行区间迭代，每迭代一步都可判断在所给区间解的存在惟一性或者是无解。这是区间迭代法的主要优点，其缺点是计算量大。

另一种方法称为不动点算法或称单纯形法，它对求解域进行单纯形剖分，对剖分的顶点给一种恰当标号，并用一种有规则的搜索方法找到全标号单纯形,从而得到方程(1)的近似解。

这种方法优点是，不要求f(□)的导数存在,也不用求逆，且具有大范围收敛性，缺点是计算量大。

参考技术A

首先定义函数:

function f=fx(x)
f(1)=3*x(1)-cos(x(2)*x(3))-0.5;
f(2)=x(1)^2-81*(x(2)+0.1)^2+sin(x(3))+1.06;
f(3)=exp(-x(1)*x(2))+20*x(3)+(10*pi-3)/3;

>> x=fsolve(@fx,[1,1,1])

最后求得
x =

0.5000    0.0000   -0.5236

扩展资料：

MATLAB是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分。

MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。

参考资料：非线性方程组数值解法百度百科

参考技术B

使用solve函数。举个例子，解非线性方程组 x^2+y^3=10 x^3-y^2=1 其中x,y为方程组的未知量 在Matlab的命名窗口中输入：

syms x y  [x y]=solve('x^2+y=10','x^2-y^2=1','x','y')

即可  输出计算结果为：  

x =       (37^(1/2)/2 + 21/2)^(1/2)     (21/2 - 37^(1/2)/2)^(1/2)  -(21/2 - 1/2*37^(1/2))^(1/2)  -(1/2*37^(1/2) + 21/2)^(1/2)     y =    - 37^(1/2)/2 - 1/2    37^(1/2)/2 - 1/2    37^(1/2)/2 - 1/2  - 37^(1/2)/2 - 1/2  

具体solve函数的使用方法，通过输入help solve来学习。

本回答被提问者采纳

如何用matlab解方程组

matlab中解方程组还是很方便的，例如，对于代数方程组Ax=b(A为系数矩阵，非奇异)的求解，MATLAB中有两种方法：
(1)x=inv(A)*b — 采用求逆运算解方程组；

(2)x=A\B — 采用左除运算解方程组
PS：使用左除的运算效率要比求逆矩阵的效率高很多~
例:
x1+2x2=8
2x1+3x2=13
>>A=[1,2;2,3];b=[8;13];
>>x=inv(A)*b
x =
2.00
3.00
>>x=A\B
x =
2.00
3.00；
即二元一次方程组的解x1和x2分别是2和3。

对于同学问到的用matlab解多次的方程组，有符号解法，方法是：先解出符号解,然后用vpa(F,n)求出n位有效数字的数值解.具体步骤如下：
第一步:定义变量syms x y z ;
第二步:求解[x,y,z,]=solve('eqn1','eqn2',,'eqnN','var1','var2','varN');
第三步:求出n位有效数字的数值解x=vpa(x,n);y=vpa(y,n);z=vpa(z,n);。
如：解二（多）元二（高）次方程组：
x^2+3*y+1=0
y^2+4*x+1=0
解法如下：
>>syms x y;
>>[x,y]=solve('x^2+3*y+1=0','y^2+4*x+1=0');
>>x=vpa(x,4);
>>y=vpa(y,4);
结果是：
x =
1.635+3.029*i
1.635-3.029*i
-.283
-2.987
y =
1.834-3.301*i
1.834+3.301*i
-.3600
-3.307。
二元二次方程组，共4个实数根；

解答如下：
基本方法是：solve(s1,s2,…,sn,v1,v2,…,vn)，即求表达式s1,s2,…,sn组成的方程组，求解变量分别v1,v2,…,vn。
具体例子如下：
x^2 + x*y + y = 3
x^2 - 4*x + 3 = 0
解法：
>> [x,y] = solve('x^2 + x*y + y = 3','x^2 - 4*x + 3 = 0')
运行结果为
x =
1 3
y =
1 -3/2

即x等于1和3；y等于1和-1.5

或
>>[x,y] = solve('x^2 + x*y + y = 3','x^2 - 4*x + 3= 0','x','y')
x =
1 3
y =
1 -3/2
结果一样，二元二方程都是4个实根。

通过这三个例子可以看出，用matlab解各类方程组都是可以的，方法也有多种，只是用到解方程组的函数，注意正确书写参数就可以了，非常方便。

2、变参数非线性方程组的求解
对于求解非线性方程组一般用fsolve命令就可以了，但是对于方程组中某一系数是变化的，该怎么求呢？

%定义方程组如下，其中k为变量
function F = myfun(x,k)
H=0.32;
Pc0=0.23;W=0.18;
F=[Pc0+H*(1+1.5*(x(1)/W-1)-0.5*(x(1)/W-1)^3)-x(2);
x(1)-k*sqrt(x(2))];

%求解过程
H=0.32;
Pc0=0.23;W=0.18;
x0 = [2*W; Pc0+2*H]; % 取初值
options = optimset('Display','off');
k=0:0.01:1; % 变量取值范围[0 1]
for i=1:1:length(k)
kk=k(i);
x = fsolve(@(x) myfun(x,kk), x0, options);%求解非线性方程组
x1(i)=x(1);
x2(i)=x(2);
end
plot(k,x1,'-b',k,x2,'-r');
xlabel('k')
legend('x1','x2') 参考技术A

用matlab求解方程组，可以用solve函数求得其解析值。

这里用a—表示α，b—表示β，c—表示θ，d—表示η

实现求解此方程组的代码：

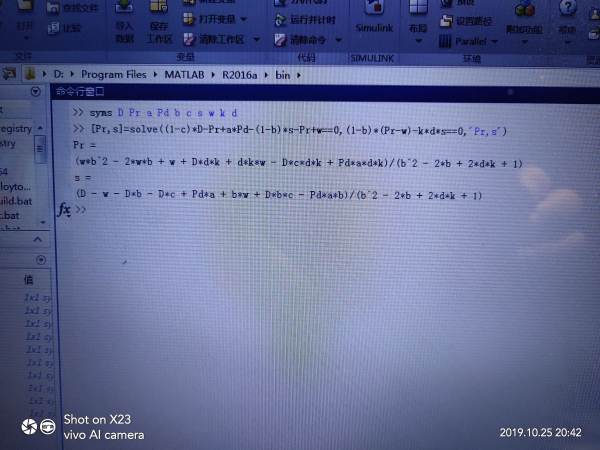
syms D Pr a Pd b c s w k d

[Pr,s]=solve((1-c)*D-Pr+a*Pd-(1-b)*s-Pr+w==0,(1-b)*(Pr-w)-k*d*s==0,'Pr,s')

运行结果

参考技术B S=solve('2*x*y=1,x+2=y+z,x+y-z=4','x,y,z'); %前面的参数是方程组列表，后面是未知变量列表
S.x %输出未知数x的值
S.y %输出未知数y的值
S.z %输出未知数z的值
f=@(x)2*x; %定义一个匿名函数y=2x，其中@(x)表示x是匿名函数的自变量
fplot(f,[-10,10]) %画图函数，第一个参数是函数名，第二参数要画函数的区间[-10,10] 参考技术C S=solve('2*x*y=1,x+2=y+z,x+y-z=4','x,y,z'); %前面的参数是方程组列表，后面是未知变量列表
S.x %输出未知数x的值
S.y %输出未知数y的值
S.z %输出未知数z的值
f=@(x)2*x; %定义一个匿名函数y=2x，其中@(x)表示x是匿名函数的自变量
fplot(f,[-10,10]) %画图函数，第一个参数是函数名，第二参数要画函数的区间[-10,10] 参考技术D 用solve函数
先举一例，解方程"x^2+100*x+99=0"
在matlab ”Command Window"中输入如下命令：
x=solve('x^2+100*x+99=0','x')
首先来求一个二元一次方程组
9x+8y=10 式1
13x+14y=12 式2
[x,y]=solve('9*x+8*y=10','13*x+14*y=12','x','y')