空间三点圆心计算公式
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了空间三点圆心计算公式相关的知识,希望对你有一定的参考价值。
已知空间3个三维坐标求圆心坐标
参考技术A 直接上代码了double a1, b1, c1, d1;
double a2, b2, c2, d2;
double a3, b3, c3, d3;
//给定的三个点
double x1, y1, z1;
double x2, y2, z2;
double x3, y3, z3;
a1 = (y1 * z2 - y2 * z1 - y1 * z3 + y3 * z1 + y2 * z3 - y3 * z2);
b1 = -(x1 * z2 - x2 * z1 - x1 * z3 + x3 * z1 + x2 * z3 - x3 * z2);
c1 = (x1 * y2 - x2 * y1 - x1 * y3 + x3 * y1 + x2 * y3 - x3 * y2);
d1 = -(x1 * y2 * z3 - x1 * y3 * z2 - x2 * y1 * z3 + x2 * y3 * z1 + x3 * y1 * z2 - x3 * y2 * z1);
a2 = 2 * (x2 - x1);
b2 = 2 * (y2 - y1);
c2 = 2 * (z2 - z1);
d2 = x1 * x1 + y1 * y1 + z1 * z1 - x2 * x2 - y2 * y2 - z2 * z2;
a3 = 2 * (x3 - x1);
b3 = 2 * (y3 - y1);
c3 = 2 * (z3 - z1);
d3 = x1 * x1 + y1 * y1 + z1 * z1 - x3 * x3 - y3 * y3 - z3 * z3;
double x, y, z, r;
x = -(b1 * c2 * d3 - b1 * c3 * d2 - b2 * c1 * d3 + b2 * c3 * d1 + b3 * c1 * d2 - b3 * c2 * d1) / (a1 * b2 * c3 - a1 * b3 * c2 - a2 * b1 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1);
y = (a1 * c2 * d3 - a1 * c3 * d2 - a2 * c1 * d3 + a2 * c3 * d1 + a3 * c1 * d2 - a3 * c2 * d1) / (a1 * b2 * c3 + a1 * b3 * c2 - a2 * b1 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1);
z = -(a1 * b2 * d3 - a1 * b3 * d2 - a2 * b1 * d3 + a2 * b3 * d1 + a3 * b1 * d2 - a3 * b2 * d1) / (a1 * b2 * c3 - a1 * b3 * c2 - a2 * b1 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1);
r = sqrt(x1 - x)*(x1 - x) + (y1 - y)*(y1 - y) + (z1 - z)*(z1 - z);
r = sqrt(x2 - x)*(x2 - x) + (y2 - y)*(y2 - y) + (z2 - z)*(z2 - z);
r = sqrt(x3 - x)*(x3 - x) + (y3 - y)*(y3 - y) + (z3 - z)*(z3 - z); 参考技术B 这个不难,不过公式忘了,讲原理吧,这个三个点确定一个三角形.然后用三角形的两条边做他们的垂直中心线.这样就ok了.
数值计算实验报告---复合求积公式(梯形抛物线龙贝格)导数求值(三点四点五点公式)
----------------------个人作业,如果有后辈的作业习题一致,可以参考学习,一起交流,请勿直接copy



··复合抛物线公式:

··龙贝格公式:



四、实验内容
------1
实验题目1中所用到的三种算法的matlab实现代码具体如下:
%复合梯形公式
function y=funct(f,n,a,b)
fi=f(a)+f(b);
h=(b-a)/n;
d=1;
for i=1:n-1
x=a+i*h;
fi=fi+2*f(x);
d=d+1;
end
f4=h/2*fi,d
%复合抛物线公式
function y=funcp(f,n,a,b)
h=(b-a)/n;
f1=0;
f2=0;
dd=1;
for i=1:n-1
dd=dd+1;
if rem(i,2)~=0;
x1=a+i*h;
f1=f1+f(x1);
else
rem(i,2)==0;
x2=a+i*h;
f2=f2+f(x2)
end
end
f3=(h/3)*(f(a)+4*f1+2*f2+f(b)),dd
%龙贝格公式
function y=romberg(f,n,a,b)
z=zeros(n,n);
h=b-a;
z(1,1)=(h/2)*(f(a)+f(b));
f1=0;
for i=2:n
for k=1:2^(i-2)
f1=f1+f(a+(k-0.5)*h);
end
z(i,1)=0.5*z(i-1,1)+0.5*h*f1;
h=h/2;
f1=0;
for j=2:i
z(i,j)=z(i,j-1)+(z(i,j-1)-z(i-1,j-1))/(4^(j-1)-1);
end
end
z,n
------2
实验题目2中所用到的三种算法的matlab实现代码具体如下:
%采用三点公式法求函数func在x0处的二阶导数
function df= ThreePoint2(func,x0,type,h)
%函数名: func
%求导点: x0
%三点公式法的形式: type
%步长:h
%导数值: df
if nargin == 3
h = 0.1;
else if (nargin == 4 && h == 0.0)
disp(\' h不能为0!\');
return;
end
end
for i=1:5
y(i) = subs(sym(func), findsym(sym(func)), x0-2*h+i*h-h);
end
hd = 1/h/h;
switch type
case 1
df = (y(3) - 2*y(4) + y(5))*hd; %用第1个公式求二阶导数
case 2
df = (y(2) - 2*y(3) + y(4))*hd; %用第2个公式求二阶导数
case 3
df = (y(1) - 2*y(2) + y(3))*hd; %用第3个公式求二阶导数
end
%采用四点公式法求函数func在x0处的二阶导数
function df= FourPoint2(func,x0,type,h)
%函数名: func
%求导点: x0
%四点公式法的形式: type
%步长:h
%导数值: df
if nargin == 3
h = 0.1;
else if (nargin == 4 && h == 0.0)
disp(\' h不能为0!\');
return;
end
end
for i=1:7
y(i) = subs(sym(func), findsym(sym(func)), x0-3*h+i*h-h);
end
hd = 1/6/h/h;
switch type
case 1
df = (12*y(4) - 30*y(5) + 24*y(6) - 6*y(7))*hd; %用第1个公式求二阶导数
case 2
df = (6*y(3) - 12*y(4) + 6*y(5))*hd; %用第2个公式求二阶导数
case 3
df = (12*y(4) - 30*y(3) + 24*y(2) - 6*y(1))*hd; %用第3个公式求二阶导数
end
%采用五点公式法求函数func在x0处的二阶导数
function df= FivePoint2(func,x0,type,h)
%函数名: func
%求导点: x0
%五点公式法的形式: type
%步长:h
%导数值: df
if nargin == 3
h = 0.1;
else if (nargin == 4 && h == 0.0)
disp(\'h不能为0!\');
return;
end
end
for i=1:9
y(i) = subs(sym(func), findsym(sym(func)), x0-4*h+i*h-h);
end
hd = 1/12/h/h;
switch type
case 1
df = (35*y(5)-104* y(6)+114* y(7)-56* y(8)+11* y(9))*hd; %用第1个公式求二阶导数
case 2
df = (11*y(4)-20* y(5)+6* y(6)+4* y(7)- y(8))*hd; %用第1个公式求二阶导数
case 3
df = (-y(3)+16* y(4)-30* y(5)+16* y(6)- y(7))*hd; %用第1个公式求二阶导数
case 4
df = (-y(2)+4*y(3)-6*y(4)+20*y(5)+11*y(6))*hd; %用第1个公式求二阶导数
case 5
df = (35*y(5)-104* y(4)+114* y(3)-56* y(2)+11* y(1))*hd; %用第1个公式求二阶导数
end
------3
%采用五点公式法求函数func在x0处的二阶导数
function df= FivePoint2(func,x0,type,h)
%函数名: func
%求导点: x0
%五点公式法的形式: type
%步长:h
%导数值: df
if nargin == 3
h = 0.1;
else if (nargin == 4 && h == 0.0)
disp(\'h不能为0!\');
return;
end
end
for i=1:9
y(i) = subs(sym(func), findsym(sym(func)), x0-4*h+i*h-h);
end
hd = 1/12/h/h;
switch type
case 1
df = (35*y(5)-104* y(6)+114* y(7)-56* y(8)+11* y(9))*hd; %用第1个公式求二阶导数
case 2
df = (11*y(4)-20* y(5)+6* y(6)+4* y(7)- y(8))*hd; %用第1个公式求二阶导数
case 3
df = (-y(3)+16* y(4)-30* y(5)+16* y(6)- y(7))*hd; %用第1个公式求二阶导数
case 4
df = (-y(2)+4*y(3)-6*y(4)+20*y(5)+11*y(6))*hd; %用第1个公式求二阶导数
case 5
df = (35*y(5)-104* y(4)+114* y(3)-56* y(2)+11* y(1))*hd; %用第1个公式求二阶导数
end

六、实验结果分析
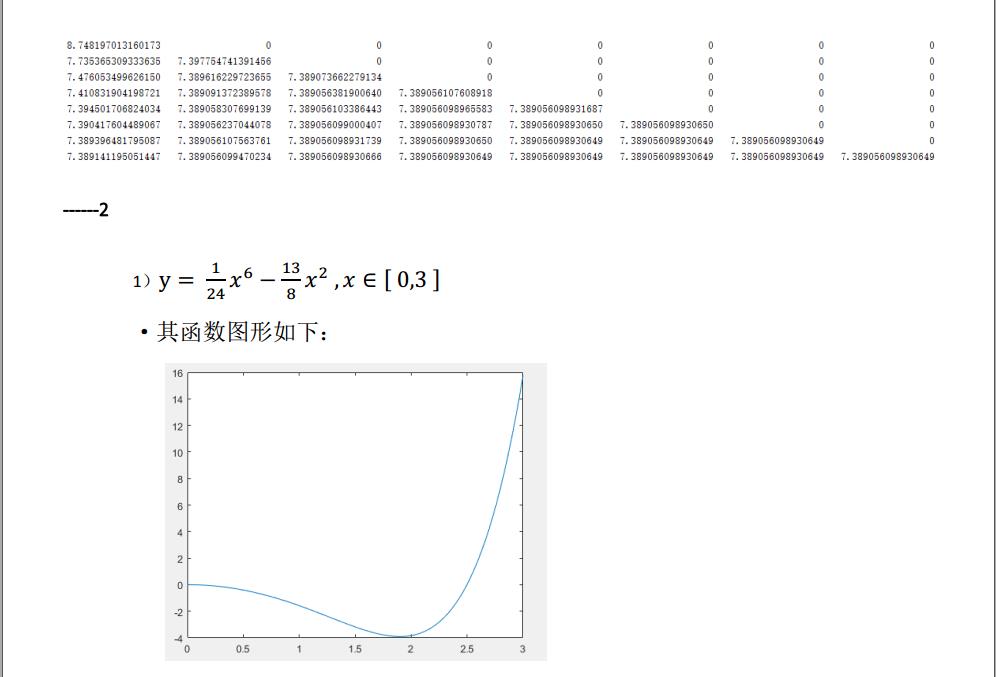
在题目一中分别使用了复合梯形公式、复合抛物线公式、以及龙贝格公式对两个题目的积分进行了求解。就结果而言,通过实验结果中的各项数据对比可以明显看出:准确度为 ----龙贝格公式>复合抛物线公式>复合梯形公式;其中龙贝格公式近乎接近正确值,精度达到了极高的标准,相比较之下,复合梯度公式的精度就比较低了。故而,在不考虑计算的时间和空间效率时,使用龙贝格公式的精度最高,效果最好;如果加上时间空间来考虑,可以采用复合抛物线公式来求解。
2.
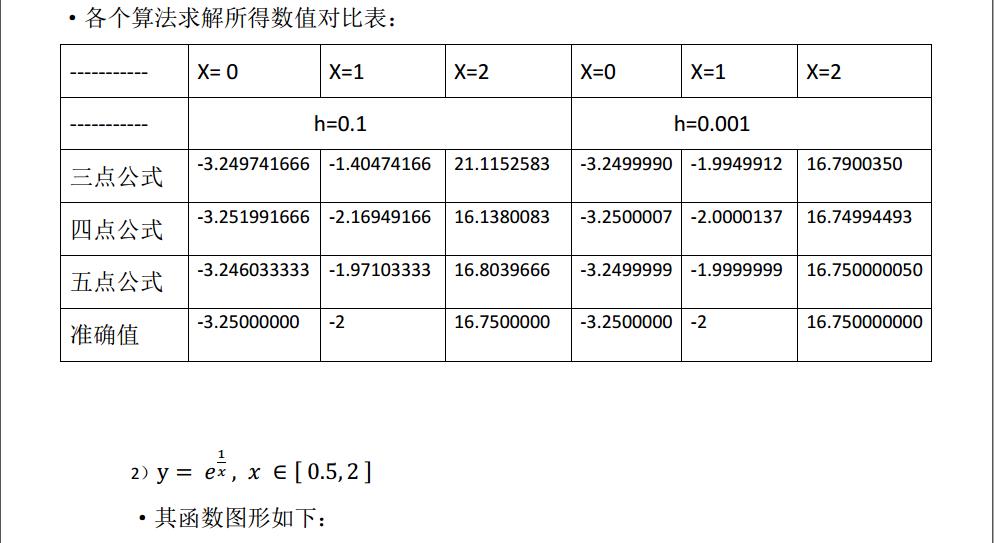
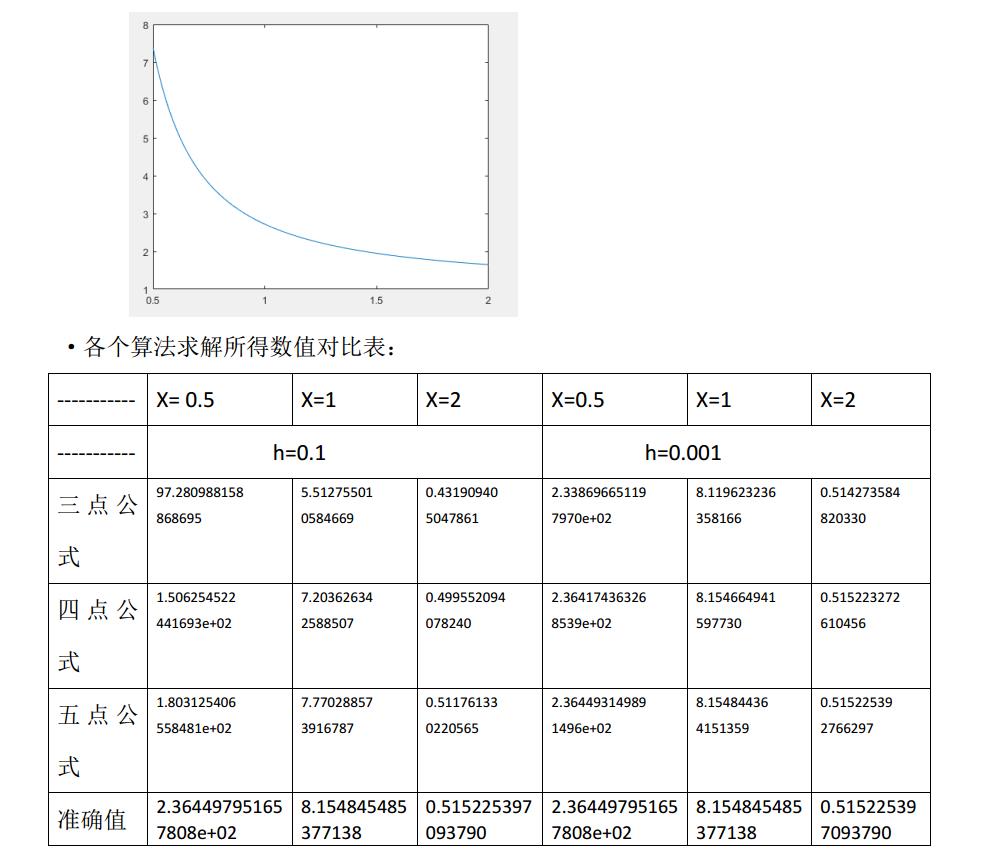
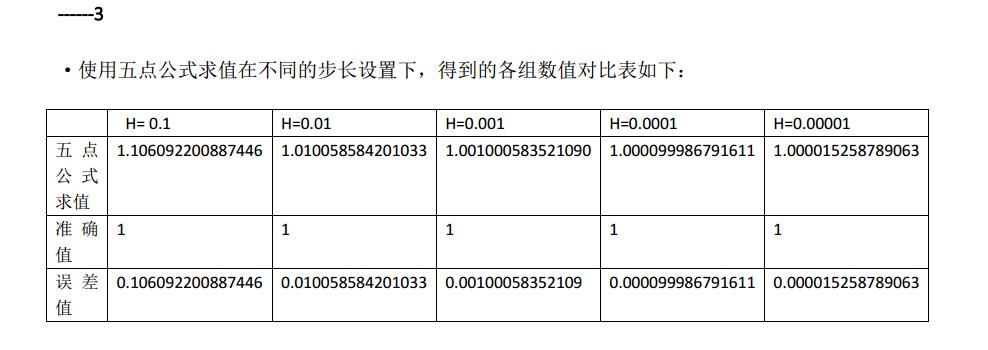
在题目二中分别使用了三点公式、四点公式、以及五点公式对两个题目的函数进行了求导,在题目三种采用了五点公式,在不同的步长设定下进行了求导。就结果而言,通过实验结果中的各项数据对比的表格可以明显看出: ·在相同的步长下,求解精度:五点公式>四点公式>三点公式; ·在同一公式下,步长越长,求解的精度会越高; ·在步长较低(h=0.1)时,三点公式所求得的导数值摆动较大,几乎无法使用; ·在取步长较高(h=0.001)时,采用五点公式,精度极高,几乎可以替代精确值使用。
---------------------------------------------------
排版依旧很别扭,截图更方便阅读,怎么说呢、、、、、凑合还能看吧
以上是关于空间三点圆心计算公式的主要内容,如果未能解决你的问题,请参考以下文章