中心化、标准化、归一化？

Posted 2023-04-19

参考技术A

图.左边是原始数据的分布情况、中间是经过中心化的分布情况、右边是经过标准化后的情况。图片来自知乎

说明：本文纯属胡说，没有加入严谨的数学推导，如有问题还请查看专业的书籍和博客文章

Zero-centered 或者 Mean-subtraction

中心化，就是把数据整体移动到以0为中心点的位置

将数据减去这个数据集的平均值。

例如有一系列的数值

计算平均值为 (1 + 3 + 5 + 7 + 9 )/ 5 = 5

数据变为

Standardization

把整体的数据的中心移动到0，数据再除以一个数。

在数据中心化之后，数据再除以数据集的标准差（即数据集中的各项数据减去数据集的均值再除以数据集的标准差）

再拿上面的数值举例

原始数据为

经过计算得到数据的标准差约为 σ = 2.8

标准化之后的结果为

Normalization

把数据的最小值移动到0，在除以数据集的最大值。

官方版

首先找到这个数据集的最大值 max 以及最小值 min ，然后将 max - min ，得到两个的差值 R ，也就是叫做 极差 ，然后对这个数据集的每一个数减去 min ，然后除以 R 。

民间版

这里你要是不记得中心化的话，先看一下中心化。然后开始，首先我们把数据仍然当做整体，然后把最小的点移动到0这个位置，然后回过头看计算公式是不是变了。由于 min 变成了 0 ，那么计算的公式就是 x / max\' ，这里的 max\' 是经过移动之后的数值。

还是拿上面的例子举例

首先用官方版的方式计算一下

原始数据

最大值 9 ，最小值 1 ，极差 9-1 = 8

接下来计算归一化后的数值

然后用民间版的方式计算一下

原始数据

按照整体把最小值移动到0，得到

然后除以最大值

可以看到，其实这个归一化还是那种计算小的占最大的比例。那么问题来了，那为什么不这样算呢?就是说不移动整体，直接把每一个数占据最大数的比例求出来不就行了吗？

也就是这样：

额，说实话，这里我觉得没什么不妥当，同样也是将数据收缩在 0~1 的范围内，但是我换了个数据好像就...

再拿一个数据

按照上面的计算，这里暂时简称为“简单除法法”

而使用归一化进行计算是这样的：

可以看到使用“简单除法法”进行计算得到的位于 0~1 范围内的数值没有经过归一化后的数据“拉得开”，好像腻乎在一块一样；同样是相对于某一数值的比例，使用归一化就不仅能将数据在收缩在 0~1 范围内，而且还让数据在这个范围内展开。这里不是太好想象为什么是这样？这样，我们打开 photoshop ，你没有看错，打开它

然后 文件 -> 新建 -> 确定 -> 新建一个图层 ，好，新建了一个，然后我们画一个方块， 矩形工具 -> 按住shift拖动 ->得到一个方块，然后 按住alt 对着方块拖动鼠标，直到拖出三个，然后按照下图所示的方式排列。

之后 按住ctrl 加选图层，把这三个方块的对应的图层都选中， 右键 -> 合并形状 。然后把三个方块拖到画布的右上角

按 ctrl + t ，可一看到在中心有一个点，这个点是变形时候的参考点，我们把点移动到 最下面这个方块 的左下角。然后把鼠标移动到缩放框的右上角 按住shift+alt 进行拖动，感受一下拖动的感觉；然后这个时候把大小还原，将那个中心点移动到这个 画布 的左下角，然后再次把鼠标移动到缩放框的右上角 按住shift+alt 进行拖动，感受一下拖动的感觉 。

中心化上面的过程我们看到了，相当于把数据 位移 了一下。在说这个之前，我们来玩一下 找不同 ，百度搜一下 找不同 ，我随便找了一张，我还记得这是朵拉，哈哈，你能快速找到不同吗？

这里有没有骚一点的操作呢？还记得上面的家伙吧你应该还没有关吧，进入 photoshop 。然后，现在你手上有 ps ，你怎么快速找不同呢？

我用 photoshop 把连在一起的两张图裁剪开，分别放到两个图层中。得到下面的图。

然后将两张图片叠在一起，就像这样，然后来回调整最上面一个图层的不透明度或者关闭打开最上面图层的眼睛，可以看到明显变化的位置就是不同啦！你可以试一下啊！

归一化、标准化可以说都是线性的，在 知乎 - 微调 的回答中，他通过公式的转变最后认为归一化、标准化很相似，都是 x + b / c 这样一种形式，具体的可以看参考中的知乎链接。对应到这篇文章中就可以这样做，你可以把那三个方块的中心点放到中心然后拖动缩放框进行缩放就是标准化啦。在说归一化、标准化的作用之前，首先来看一句话

看这句话我就想起了我们和宇宙的“体型”的极大悬殊，宇宙浩瀚无垠，极其庞大；沙粒，微乎其微，极其渺小。另外除了上面这句话之外，还有“一花一世界，一叶一菩提”也比较常听到，这种“以小见大”的境界其实有一种理论模型的说法，我记得在一些初高中的化学或者物理课本上都画有原子图，中心一个原子核，然后又三个电子围绕着中心旋转，我相信很多人脑子里只要有过太阳系和这幅原子图的映像后会将它们联系起来。

原子 的半径为 10^(-10) m ，太阳系的半径为 6*10^(12)m ，它们的“体型”的差别用“天壤之别”似乎也不够，但是这种内部的“运转”形式又是如此的相似，难道说我们这个世界存在着一种特殊的规律？其实之前就有人提出过一个观念，叫做 分形宇宙(Fractal Universe) 。

这个是混沌动力学里面研究的一个饶有兴趣的课题，它给我们展现了复杂的结构如何在不同层面上一再重复。所谓的分形宇宙也只是一家之言罢了。

读到这里，你的脑海中是不是已经浮现出了一个“小宇宙”、“大原子”呢？你的脑子是不是进行了一次归一化或者说标准化的过程呢？

最近回过头来看看之前写的，没有特别说明其中归一化与标准化的中的差别。另外也发现标准化与归一化的形式还不单单只是一种。

说明：公式截取自 机器学习中的特征缩放（feature scaling）浅谈

可以看到最前面两种（Rescaling 和 Mean normalisation）与前面说到的归一化是相似的，我觉这里这两个可以归为一类。

它们的分母是是一样的，都是 max(X) - min(X) ，也就是说它们以自己内部的最大的差距最为分母，但是分子不一样，分别是 x - min(X) 和 x - mean(X) ，这是个什么意思呢？

这里的 x - mean(X) 就是之前说到的 中心化 ！

因为分母相同，这里先暂时不管分母。

假如有六个点，在每条路上都一条标杆，这里我们来计算一下每一个距离标杆的长度

以 x - min(X) 计算距离

以 x - mean(X) 计算距离

通过图来看， x - min(X) 中的 min(X) ， x - mean(X) 中的 mean(X) 是两幅图中各自的标杆，如果移动这条标杆的位置就可以互相转换。所以这两个是相似的。但是我们可以看到，第一种得到的数值均为 正数 ，但是第二种是有 正负值的 ，分布于均值两侧。

那么第三种呢？这个对应到上面我们说到的标准化的东西。但是与上面归一化有什么差别呢？

我们拿第二种（Mean normalisation）与第三种（Standardization ）进行对比会比较好理解，这两个的分子都是相同的，但是分母不同，前者是 max(X) - min(X) （也就是极差），后者是 std(X) （也就是标准差），我们看看这两者的计算方式的特点

如果说数据存在特别大的或者特别小的数据的时候，归一化可能会导致数据黏糊在一起的情况（因为归一化的分母始终是数据中距离最大的点的距离），但是标准化（不仅仅会考虑单个极其特别的点，其他的点都会考虑，得到）出现这种情况会好一些（特别是数据量较大的情况下可能会抹除奇异值的影响）。

另外，归一化求得的数值最后会在 [-1, 1] 之间，而标准化不一定，有可能会大于 1 或者小于 -1 。

中间如果有错误，望能告知。

版权声明 ：本文采用 知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议 (CC BY-NC-ND 4.0) 进行许可。

Sklearn标准化和归一化方法汇总：标准化 / 标准差归一化 / Z-Score归一化

Sklearn中与特征缩放有关的五个函数和类，全部位于sklearn.preprocessing包内。作为一个系列文章，我们将逐一讲解Sklearn中提供的标准化和归一化方法，以下是本系列已发布的文章列表：

• Sklearn标准化和归一化方法汇总(1)：标准化 / 标准差归一化 / Z-Score归一化
• Sklearn标准化和归一化方法汇总(2)：Min-Max归一化
• Sklearn标准化和归一化方法汇总(3)：范数归一化

以下是Sklearn中的五种与特征缩放相关的函数和类，我们的研究也是为围绕这些函数和类展开的：

名称	方法名	类名
标准化 / Z-Score 归一化 / 标准差归一化	sklearn.preprocessing.scale	sklearn.preprocessing.StandardScaler
Min-Max 归一化	sklearn.preprocessing.minmax_scale	sklearn.preprocessing.MinMaxScaler
范数归一化	sklearn.preprocessing.normalize	sklearn.preprocessing.Normalizer
Robust Scaler（无常用别名）	sklearn.preprocessing.robust_scale	sklearn.preprocessing.RobustScaler
Power Transformer （无常用别名）	sklearn.preprocessing.power_transform	sklearn.preprocessing.PowerTransformer

关于各种关于标准化和归一化的概念和分类，我们已经在此前一篇文章《标准化和归一化概念澄清与梳理》中做了详细的梳理和澄清，不清楚的读者可以先阅读一下此文。本文我们研究第一种归一化手段：标准化 / 标准差归一化 / Z-Score归一化。本文地址：https://laurence.blog.csdn.net/article/details/128713962，转载请注明出处！

1. 算法

标准化 / 标准差归一化 / Z-Score归一化的算法是：先求出数据集（通常是一列数据）的均值和标准差，然后所有元素先减去均值，再除以标准差，结果就是归一化后的数据了。经标准差归一化后，数据集整体将会平移到以0点中心的位置上，同时会被缩放到标准差为1的区间内。要注意的是数据集的标准差变为1，并不意味着所有的数据都会被缩放到[-1,1]之间，下文有示例为证。其计算公式如下（其中$\mu$是均值，$\sigma$是标准差）：

$$x^{{}^{\prime }}=\frac{x-\mu }{\sigma }$$

2. 示例

在下面的示例中，我们准备了一组身高数据，这组数据符合以170为均值，170*0.15为标准差的正态分布。我们会通过三种方法计算出标准差归一化后的数据，从中我们可以理解标准差归一化的计算逻辑并掌握直接进行标准差归一的工具方法和类，以下是示例将要演示的3种计算方法：

1. 根据公式手动计算
2. 使用sklearn.preprocessing.scale直接处理
3. 使用sklearn.preprocessing.StandardScaler直接处理

以下是示例代码：

# 标准差归一化 / Z-Score归一化 / 标准化

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
from sklearn.preprocessing import StandardScaler
# author: https://laurence.blog.csdn.net/

%matplotlib inline
np.random.seed(42)
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(12,5))

heights = np.random.normal(loc=170, scale=170*0.15, size=1000)

print("1. 原始数据")
print(f"heights (first 3 elements) = heights[:3]")
print(f"heights mean = heights.mean()")
print(f"heights standard deviation = heights.std()")

ax1.hist(heights, bins=50)
ax1.set_title("raw data")
ax1.annotate(f"σ = heights.std()", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("2. 根据公式手动进行标准差归一化（标准化）")
std_scaled_heights = (heights - heights.mean()) / heights.std()
print(f"std_scaled_heights (first 3 elements) = std_scaled_heights[:3]")
print(f"std_scaled_heights standard deviation = std_scaled_heights.std()")

ax2.hist(std_scaled_heights, bins=50)
ax2.set_title("manually scaled")
ax2.annotate(f"σ = std_scaled_heights.std()", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("3. 使用scale函数进行标准差归一化（标准化）")
std_scaled_heights = scale(heights)
print(f"std_scaled_heights (first 3 elements) = std_scaled_heights[:3]")
print(f"std_scaled_heights standard deviation = std_scaled_heights.std()")

ax3.hist(std_scaled_heights, bins=50)
ax3.set_title("scale()")
ax3.annotate(f"σ = std_scaled_heights.std()", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("4. 使用StandardScaler函数进行标准差归一化（标准化）")

# 在交付给Scaler前，需将一维数据转置为二维单列数组，以便适配Scaler接受的二维数组结构和轴向，即：按列进行缩放（axis=0)
# 受上层Transformer接口的约束，所有Scaler均不接受axis参数，默认按列计算，如要不想或不便转换，可以使用scale(axis=)函数进行缩放
heights = heights.reshape(-1,1)

std_scaled_heights = StandardScaler().fit_transform(heights)
print(f"std_scaled_heights (first 3 elements) = std_scaled_heights[:3].tolist()")
print(f"std_scaled_heights standard deviation = std_scaled_heights.std()")

ax4.hist(std_scaled_heights, bins=50)
ax4.set_title("StandardScaler")
ax4.annotate(f"σ = std_scaled_heights.std()", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

plt.show()

输出数据：

1. 原始数据
heights (first 3 elements) = [182.6662109  166.47426032 186.51605772]
heights mean = 170.49296742346928
heights standard deviation = 24.957518297557534
--------------------------------------------------------------------------------------------------------------
2. 根据公式手动进行标准差归一化（标准化）
std_scaled_heights (first 3 elements) = [ 0.48775857 -0.1610219   0.64201457]
std_scaled_heights standard deviation = 1.0
--------------------------------------------------------------------------------------------------------------
3. 使用scale函数进行标准差归一化（标准化）
std_scaled_heights (first 3 elements) = [ 0.48775857 -0.1610219   0.64201457]
std_scaled_heights standard deviation = 1.0
--------------------------------------------------------------------------------------------------------------
4. 使用StandardScaler函数进行标准差归一化（标准化）
std_scaled_heights (first 3 elements) = [[0.48775857171297676], [-0.16102190351705692], [0.6420145667955481]]
std_scaled_heights standard deviation = 1.0

输出图表：

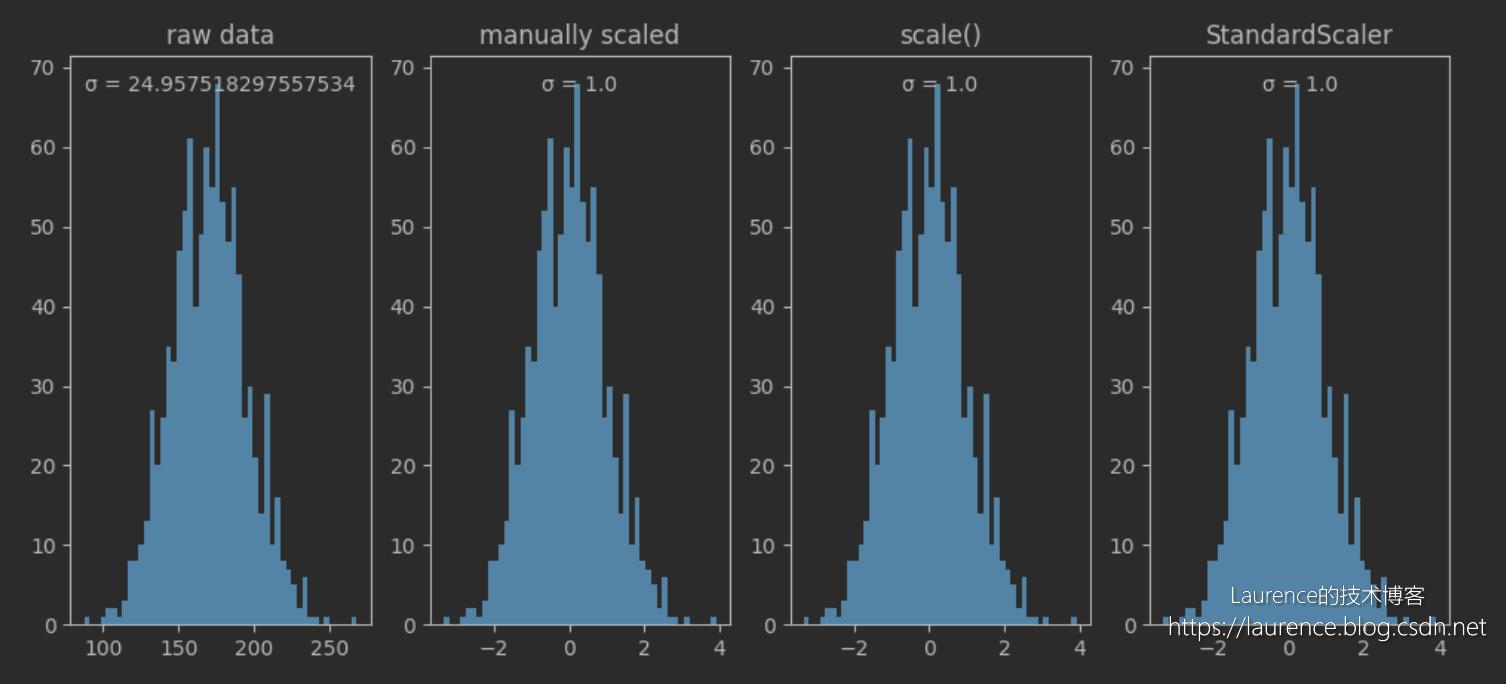
3. 解读

从输出的直方图可以看到：经过标准差归一化后，数据集被平移到了0点为中心的位置上，数据的方差从原来的24.96归置为1，数据分布（直方图形状）不变。关于标准差归一化提醒两个容易无解的地方：

• 经标准差归一化处理后，数据集的总体标准差变为1，而不是所有数据都会被收缩到[-1,1]之间，上图即是一个证明
• 标准差归一化处理不会改变数据分布，这一点很多文章的说法都是错误的，如果原来的数据就不符合正态分布，缩放后的数据依然不会符合(当然，严格的说均值和标准差改变的话，分布也会变，但是分布类型是不会被改变的，原来是什么类型，缩放后还是什么类型)

最后，提醒一下StandardScaler的使用方法：sklearn.preprocessing包内的Scaler类均不接受一维数组，在将一维数组传给Scaler前，需将其转置为（只有一列的）二维数组；此外，受上层Transformer接口的约束，所有Scaler均不接受axis参数，默认按列计算，如要不想或不便转换，可以使用对应函数进行按行缩放（此类场景并不常见），对应函数有axis参数。