蓝桥杯第26天（Python）考前挣扎

Posted 2023-04-12 Jin、焯

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了蓝桥杯第26天（Python）考前挣扎相关的知识，希望对你有一定的参考价值。

题型：

1.思维题/杂题：数学公式，分析题意，找规律

2.BFS/DFS：广搜（递归实现），深搜（deque实现）

3.简单数论：模，素数（只需要判断到 int（sqrt（n））+1），gcd，lcm，快速幂（位运算移位操作），大数分解（分解为质数的乘积）

4.简单图论：最短路（一对多（Dijstra，临接表，矩阵实现），多对多（Floyd，矩阵实现）），最小生成树（并查集实现）

5.简单字符串处理：最好转为列表操作

6.DP：线性DP，最长公共子序列，0/1背包问题，最长连续字符串，最大递增子串

7.基本算法：二分，贪心，组合，排列，前缀和，差分

8.基本数据结构：队列，集合，字典，字符串，列表，栈，树

9.常用模块：math，datetime，sys中的设置最大递归深度（sys.setrecursionlimit(3000000)），collections.deque（队列），itertools.combinations（list,n）（组合），itertools.permutations（list,n）（排列） heapq（小顶堆）

题型：

模板回顾：

1.DFS代码框架（搜图建议↓为x方向，→为y方向）（找有多少条路径）

4.DP动态规划（完全背包 http://t.csdn.cn/HnkGN）（ http://t.csdn.cn/jSSby）

8.图论算法（图论章节http://t.csdn.cn/pitI6）

模板回顾：
1.DFS代码框架（搜图建议↓为x方向，→为y方向）（找有多少条路径）

（BFS章节：http://t.csdn.cn/iv8UO）

标记数组，记录数组，全局变量ans

搜路径模板

搜索组合模板

BFS+DFS

import sys  #设置递归深度
import collections  #队列
import itertools  # 排列组合
import heapq
sys.setrecursionlimit(100000)
 
s="01010101001011001001010110010110100100001000101010 \\
10000001100111010111010001000110111010101101111000"
 
 
vis=[[0]*60 for _ in range(60)]  # 标记是否访问过
fa=[['']*60 for _ in range(60)]  # 记录父结点
flag=['D','L','R','U']  # ↓x → y
##a = list(s.split(' '))
##print(a)
##ss=[]
##for i in s:  #转为2维列表
##    ss.append(i)
##print(ss)
ss=[]
for i in range(30):
    ss.append(list(map(int,input())))
 
 
def dfs(x,y):  # 通过DFS遍历找路径
    if x==0 and y==0:
        return
    if fa[x][y]=='D':dfs(x-1,y)
    if fa[x][y] =='L': dfs(x,y+1)
    if fa[x][y] =='R': dfs(x,y-1)
    if fa[x][y] =='U': dfs(x+1,y)
    print(fa[x][y],end='')
    
def bfs(x,y):
    global fa
    global vis
    deque=collections.deque()
    walk=[[1,0],[0,-1],[0,1],[-1,0]]  # 下，左，右，上
    vis[x][y]=1
    deque.append((0,0))  # 添加进队列
    while deque:
        x,y=deque.popleft()
        #print(x,y)
        if x==29 and y==49:
            print("找到终点！！")
            break
        for index in range(4):
            dx,dy=walk[index]
            nx=x+dx;ny=y+dy
            if 0<=nx<=29 and 0<=ny<=49 :
                if vis[nx][ny]==0 and ss[nx][ny]==0: # 坐标合法且没有走过
                    vis[nx][ny]=1
                    deque.append((nx,ny))
                    fa[nx][ny]=flag[index]
 
bfs(0,0)    
dfs(29,49)

用栈记录路径，即在保护现场是入栈，恢复现场时出栈。

2.BFS逐层搜索（找最短路径）

（BFS章节：http://t.csdn.cn/G1kgx）

搜索模板

BFS搜索示例（通过set（）去重）

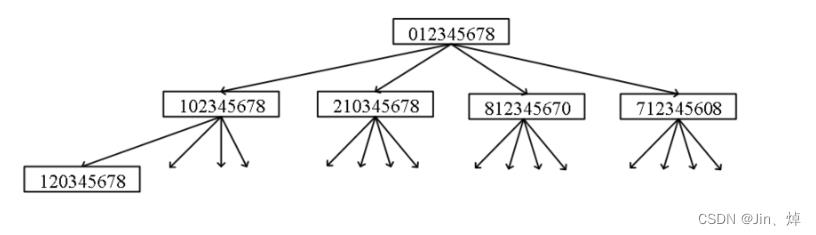
3.并查集（连通子图，最小生成树）

4.DP动态规划（完全背包 http://t.csdn.cn/HnkGN）（ http://t.csdn.cn/jSSby）

0/1背包问题：

def solve(N,C):  # 从左到右，从上到下 （先种类，再体积）
    for i in range(1,N+1): # N种物品，先1种，再2种......
        for j in range(1,C+1):  # 当前背包体积
            if c[i]>j : dp[i][j] = dp[i-1][j]    # 新增的第i种物品的体积大于背包重量，只有不选，继承上一个选择
            else: dp[i][j] = max(dp[i-1][j-c[i]]+w[i],dp[i-1][j])  # 装或者不装，找最大值
            
    return dp[N][C]
N,C= map(int,input().split())
n=3010
dp = [[0]*n for i in range(n)]  # 初始化dp数组，预留更大空间
c=[0]*n  # 记录体积
w=[0]*n # 记录价值
for i in range(1,N+1):   #读入N种物品的价值和体积
    c[i],w[i] = map(int,input().split())
print(solve(N,C))

最长公共子序列

n,m = map(int,input().split())  # B n个元素 A m个元素
a = [0] + list(map(int,input().split()))
b = [0] + list(map(int,input().split()))
dp = [[0]*(m+1) for _ in range(2)]   # 注意这里是m,不是n
now = 0 ;old = 1
for i in range(1,n+1):
    now,old = old,now
    for j in range(1,m+1):
        dp[now][j] = max(dp[now][j-1],dp[old][j])
        if a[i]==b[j]:  # 相同的元素
            dp[now][j] = max(dp[now][j],dp[old][j-1]+1)
print(dp[now][m])

最长递增子序列（LIS）

N =int(input()) # 对手个数
a = [0]+[int(i) for i in input().split()]  # 记录对手战力值
dp = [0]*(N+1) # 记录以第i个数为结尾的最长递增子序列
dp[1]=1
for i in range(2,N+1):  # 从2-N循环
    for j in range(1,i): # 查找前面的比a[i]小的
        if a[j]<a[i] and dp[j]>dp[i]:   #找到小的同时给他赋值max（dp[j]）
            dp[i]=dp[j]
        dp[i]+=1  # 加1,即本身

编辑距离（字符串转换）

5.数论

LCM和GCD

快速幂

位运算
通过 n&1=True，则n最低位就是1
n>>,n右移动
 
def fast(a,n,mod):
    ans=1
    a%=mod   # 提升运算效率，Python不用担心大数月越界问题
    while(n)>0：
        if n&1 :
            ans=(a*ans)%mod
        #a=a*a   # 翻倍
        a=(a*a)%mod   # 翻倍
        n=n>>1  # 右移一位
a,b,mod = map(int,input().split())
print(fast(a,b,mod))

矩阵乘法

埃式筛

大数分解（质因数分解）

import sys  #设置递归深度
import collections  #队列
import itertools  # 排列组合
import heapq  #小顶堆
import math
sys.setrecursionlimit(300000)
 
 
#对一个数进行大数分解
ans=0
n=int(input())
for i in range(2,int(math.sqrt(n))+1):
   if n%i==0:  #发现质数
      ans+=1
      #print(i)  # 打印质数约数
      while n%i==0:  # 消除这个质数
         n=n//i
if n>1:
   #print(n)  # 打印质数约数
   ans+=1
print(ans)

6.组合数学

加法原理

鸽巢原理

杨辉三角

import os
import sys
 
# 骗分写法
n=int(input())
a=[[1],[1,1]]
for i in range(1,500): # 50-1+2行
  b=[]
  temp=0
  for j in range(i): # 根据上一行i计算
    temp=a[i][j]+a[i][j+1]
    b.append(temp)
  a.append([1]+b+[1])
# print(a)
b=[]
for i in range(501):  #进行队列拼接
    b=b+a[i]
print(b.index(n)+1)  # 直接通过队列值找索引

import os
import sys
 
# 请在此输入您的代码
n=[0,1,1,1,1,2,1]
#n=[[0],[1,1],[1,2,1]]
last=[1,2,1]
for i in range(50):
  new=[]
  for a,b in zip(last+[0],[0]+last):
    new.append(a+b)
  n.append(new)
  last=new
 
m=int(input())
print(n.index(m))

7.计算几何

点积

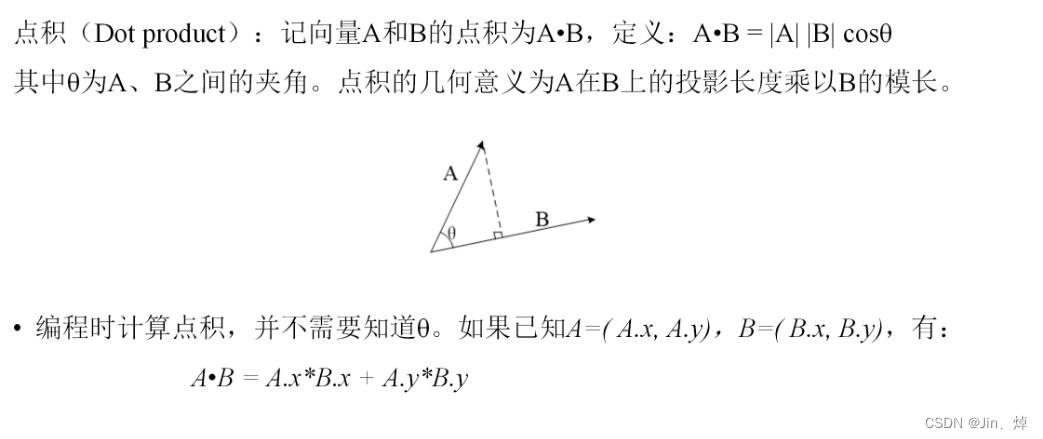
叉积

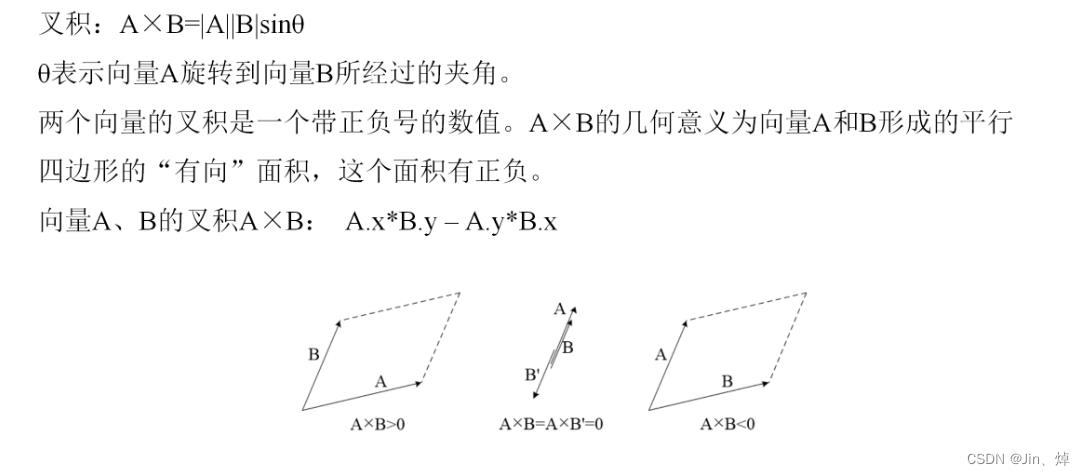
点跟直线关系

8.图论算法（图论章节http://t.csdn.cn/pitI6）

存边方式

数组存边

临接矩阵

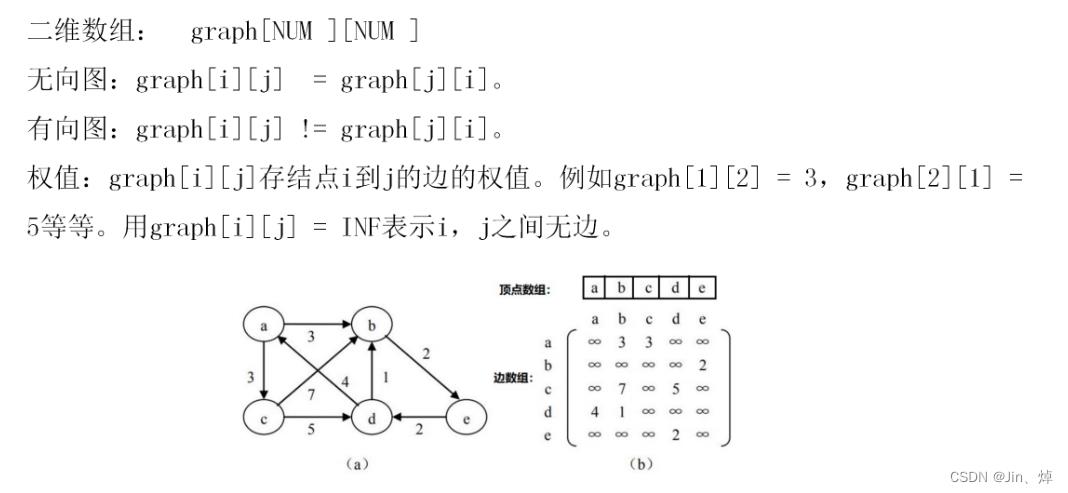邻接表

Floyd算法

import os
import sys
 
# 请在此输入您的代码
#floyd算法，多对多
 
 
def floyd():
  global dp
  for i in range(1,n+1):
    for j in range(1,n+1):
      for k in range(1,n+1):
        dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
 
n,m,q = map(int,input().split())
inf=2**120
dp=[[inf]*(n+1) for i in range(n+1)]
choice=[]
for i in range(m):
  u,v,w=map(int,input().split())
  dp[u][v]=w
  dp[v][u]=w
for i in range(q):
  s,d = map(int,input().split())
  choice.append((s,d))
floyd()
for s,d in choice:
  if dp[s][d]!=inf:
    print(dp[s][d])
    continue
  print(-1)

Dijstra算法

import heapq  # 导入堆
def dij(s):
    done=[0 for i in range(n+1)]  # 记录是否处理过
    hp=[]  #堆
    dis[s]=0
    heapq.heappush(hp,(0,s))   #入堆，小顶堆
    while hp:
        u=heapq.heappop(hp)[1] #出堆元素结点
        if done[u]: #当前结点处理过
            continue
        done[u]=1
        for i in range(len(G[u])): #遍历当前结点的邻居
            v,w =G[u][i]
            if done[v]:continue
            dis[v]=min(dis[v],dis[u]+w)  # 更新当前结点邻居的最短路径
            heapq.heappush(hp,(dis[v],v))
 
 
 
 
n,m = map(int,input().split())#
s=1  # 从1开始访问
G=[[]for i in range(n+1)]   #邻接表存储
inf = 2**50
dis = [inf]*(n+1) #存储距离
for i in range(m):# 存边，这里是单向边
    u,v,w = map(int,input().split())
    G[u].append((v,w))  #记录结点u的邻居和边长
 
dij(s)
for i in range(1,n+1):
    if dis[i]==inf:
        print("-1",end=' ')
    else:
        print(dis[i],end=' ')

import sys  #设置递归深度
import collections  #队列
import itertools  # 排列组合
import heapq  #小顶堆
import math
sys.setrecursionlimit(300000)
 
 
 
def dij():
   dist[1]=0  #很重要
   for _ in range(n-1): # 还有n-1个点没有遍历
      t=-1
      for j in range(1,n+1):
         if st[j]==0 and (t==-1 or dist[t]>dist[j]):  #找到没处理过得最小距离点
            t=j
      for j in range(1,n+1):
         dist[j]=min(dist[j],dist[t]+gra[t][j])  # t-j的距离，找最小值
      st[t]=1  # 标记处理过
   return dist[n]
      
n,m=map(int,input().split())
 #下标全部转为从1开始
stay=[0]+list(map(int,input().split()))
stay[n]=0   
gra = [[float('inf')] * (n+1) for _ in range(n+1)]
dist = [float('inf')] * (n+1)
st=[0]*(n+1)  # 标志是否处理
 
 
for i in range(m):
   u,v,w=map(int,input().split()) #这里重构图
   gra[u][v]=stay[v]+w
   gra[v][u]=stay[u]+w
 
 
print(dij())

Bellman-ford算法

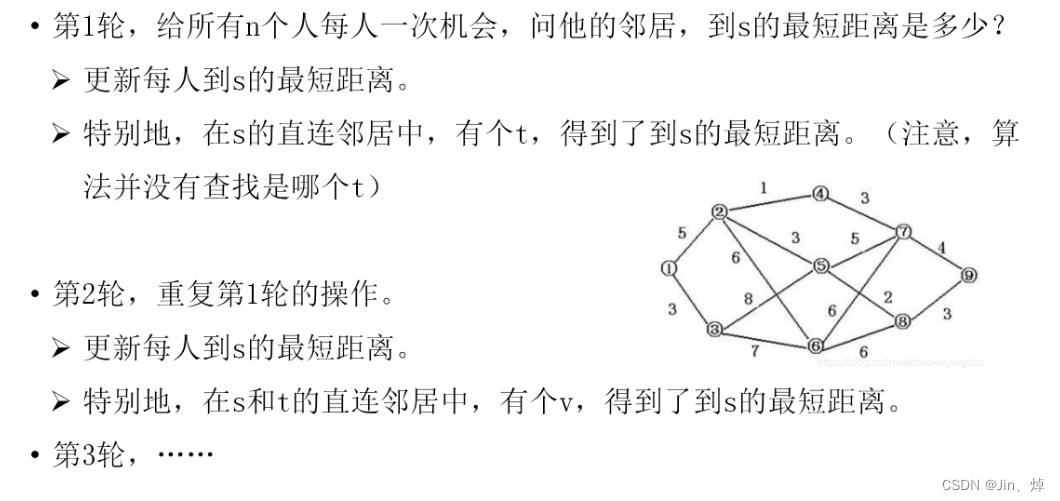
n,m=map(int,input().split())
t=[0]+list(map(int,input().split()))
e=[]  #简单的数组存边
 
for i in range(1,m+1):
    a,b,c = map(int,input().split())
    e.append([a,b,c])  # 双向边
    e.append([b,a,c])
 
dist=[2**50]*(n+1)
dist[1]=0
 
for k in range(1,n+1): # 遍历每个点，n个点，执行n轮问路
    for a,b,c in e:  # 检查每条边，每一轮问路，检查所有边
        res=t[b]
        if b==n:
            res=0
        dist[b]=min(dist[b],dist[a]+c+res)  # 更新路径长度
 
print(dist[n])

9.常用库

math

datetime datetime.date() date.days() date.timedelta

sys中的设置最大递归深度（sys.setrecursionlimit(3000000)） sys.exit()

collections.deque（队列）

itertools.combinations（list,n）（组合），itertools.permutations（list,n）（排列）

heapq（小顶堆） heapq.heappush(list,(0,s)) # 将list堆化，向list添加元素（0，s）

10.前缀和、差分

http://t.csdn.cn/rQs6M

第十四届蓝桥杯第二期模拟赛 python

第十四届蓝桥杯第二期模拟赛【python】

文章目录

第十四届蓝桥杯第二期模拟赛【python】

答案仅供参考哦，不要全信哈哈，应该是全部完成，最后一题第十题应该也是标程，真不错！！！祝大家都能马到成功

2022/11/22 模拟赛前5道填空题已更新完成，6-8题酌情写完，其他先放着，等有空看看

2022/11/24 早上顺手把第9题写完了，只剩下第十题

2022/11/24 不想空着，也用树状数组把最后第十题给解决了，完美收官

✨最小的2022 (python二进制)

❓️问题描述

请找到一个大于 2022 的最小数，这个数转换成二进制之后，最低的 6个二进制为全为 0。
请将这个数的十进制形式作为答案提交。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题和第一期模拟赛的第一题都是考虑到了二进制，对于python来说，还是很快的，只需要从2022开始遍历，利用python的bin函数，就可以迅速将十进制转成二进制，然后再减去首字母的两个0b即可，判断最低的6个尾数为0即可。

🖥︎参考答案

2048

i = 2022
while True:
    if bin(i)[-6:] == '000000':
        print(i)
        break
    i += 1

✨经过天数（datetime库）

❓️问题描述

我们计从1949 年10月1日至 1949 年10月2日为经过了1天

请问从1949年10月1日至2022年1月1日经过了多少天?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题我觉得有很多种方法，可以直接手算，但是对于python来说，还是很简单，其实就是一个日期相减而已，得到天数即可，善用datetime库，人生如此美好

datetime参考资料

Python–time, datetime库常用方法
 python——datetime库用法

🖥︎参考答案

26390

import datetime
d1 = datetime.datetime(2022,1,1)     # 第一个日期
d2 = datetime.datetime(1949,10,1)    # 第二个日期
interval = d1 - d2                   # 两日期差距
print(interval.days)                 # 具体的天数

✨特殊的十六进制数（int16进制）

❓️问题描述

8518 是一个非常特殊的数，如果把这个数看成 16 进制数，它的值为 $(8518) 16 = 8 * 16 * 16 * 16 + 5 * 16 * 16 + 1 * 16 + 8 = 34072$ ，而34072 正好是 8518 的整数倍
9558 也是这样一个数，当看成 16 进制时是 38232。
其实长度为 1的数0到9 都满足看成 16 进制后是自己的整数倍 (1倍)。
请问，除开长度为 1的数，最小的满足这样条件的数是多少?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题对于python来说，求16进制还是比较简单的，可以用int快速求解我们的16进制，然后判断两者的关系。我们要取最小的，也就是从10开始取其，取到就break即可，人生苦短，我选python

🖥︎参考答案

1038

i = 10
while True:
    h = int(str(i), 16) # 算出16进制的数
    if h%i == 0:
        print(i)
        break
    i += 1

✨矩阵的最小路径（DP/DFS)

❓️问题描述

小蓝有一个 30 行 60 列的数字矩阵，矩阵中的每个数都是 0 到 9 之间的数字。
　　174094882455171152761423221685761892795431233411387427793198
　　650286024865090061389344606618496378829135984076361542097372
　　601657541200146071777733599818266038012509478351201640618984
　　143988087783837107349651099683484992553337438088068198972282
　　890781586124258626539246182119762952003918195325258677229419
　　698255491250839396799769357665825441616335532825361862146291
　　503649293440596342887581257444442930778730382520372975343211
　　325351222640703400531067500454956482168314849207060705673849
　　265774579830223671554026061117300483012903885770893074783710
　　083450145620356667677191627276513995926532444279237315785832
　　411595106453089134746365281031552217482363035280722591085079
　　053410485925413958279617719034175332412908745680774313630190
　　429314820559328748143552689295945058801322270313370955837837
　　939182801848609300876356583948397645861551964542532682663945
　　625356614462682551015176002433628234343684739800880514363921
　　982340231989891351425389287014819359798014755509282450440511
　　590838726938103384801541373585690893606978941566666714061214
　　952341523168827712604946036245881214982452998386986623826275
　　782780208928205527678781609589000725521486468983551558405472
　　149903035076783644195574734088152324666290493119955560594634
　　905391288186024902215444250421277955403412298227858394469856
　　607272647132163832860126054679347881638761723785858733108109
　　249157334220127702410373959720286708183036202841837581704881
　　367895556630088230650972282944827258473951902831431040790814
　　079538232104075905120989173307660289899942087873076421916033
　　622143260549608274076012938515668898707915863945382394851328
　　164677964192631597026176253407553188801750590935427267220117
　　591817866992665840378311257621611574856498432538327068011953
　　631534031790352912617015229051836886166704989498756486878095
　　690013558017746707412183571476823027885971347137127534455141
　　现在小蓝想从这个矩阵的第一行第一列画一条折线到第 30 行 60 列，线只能沿水平向右走或竖直向下走，只能在有数字的地方拐弯。小蓝想知道，这样一条线经过的数字的和最大是多少。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题第一感觉就是以搜索问题，算最大的情况，这道题可以暴力解决或者直接用搜索

但是我尝试用暴力感觉好像有点慢，然后我写了个DFS搜索进行，但是如果不剪枝实在是太慢了，我就思考了一下，首先我们这个dfs不需要标记数组的，因为根本不会往回走

第二，我设计了一个记录数组，记录走到当前最大的值，然后其他走到当前都没有他大，那肯定不继续搜索了，因为后续的加减都是一样的，这样就完成了一个剪枝的策略。速度就很快

这道题开始比上一次质量高了，需要用对应的算法才可以解，要不然只能用暴力，不过也可以，只是花的时间长一点，应该也可以接受

除此之外呢，其实这个DFS仔细一看，就是一个dp而已，所以我们可以把DFS更加简便，很快就可以得到结果

🖥︎参考答案

592

DFS方法

m = '''174094882455171152761423221685761892795431233411387427793198
650286024865090061389344606618496378829135984076361542097372
601657541200146071777733599818266038012509478351201640618984
143988087783837107349651099683484992553337438088068198972282
890781586124258626539246182119762952003918195325258677229419
698255491250839396799769357665825441616335532825361862146291
503649293440596342887581257444442930778730382520372975343211
325351222640703400531067500454956482168314849207060705673849
265774579830223671554026061117300483012903885770893074783710
083450145620356667677191627276513995926532444279237315785832
411595106453089134746365281031552217482363035280722591085079
053410485925413958279617719034175332412908745680774313630190
429314820559328748143552689295945058801322270313370955837837
939182801848609300876356583948397645861551964542532682663945
625356614462682551015176002433628234343684739800880514363921
982340231989891351425389287014819359798014755509282450440511
590838726938103384801541373585690893606978941566666714061214
952341523168827712604946036245881214982452998386986623826275
782780208928205527678781609589000725521486468983551558405472
149903035076783644195574734088152324666290493119955560594634
905391288186024902215444250421277955403412298227858394469856
607272647132163832860126054679347881638761723785858733108109
249157334220127702410373959720286708183036202841837581704881
367895556630088230650972282944827258473951902831431040790814
079538232104075905120989173307660289899942087873076421916033
622143260549608274076012938515668898707915863945382394851328
164677964192631597026176253407553188801750590935427267220117
591817866992665840378311257621611574856498432538327068011953
631534031790352912617015229051836886166704989498756486878095
690013558017746707412183571476823027885971347137127534455141'''

m = m.split('\\n')
record = [[0]*60 for _ in range(30)] # 记录数组，标记经过此最大数字
for i in range(30):
    for j in range(60):
        record[i][j] = int(m[i][j]) # 默认是当前数字
# print(vis)
f = [(1,0), (0,1)] # 向右搜索 + 向下搜索

ans = 0

# 判断是否合法
def check(x,y):
    if 0 <= x <= 29 and 0 <= y <= 59:
        return True
    return False

# 从x,y开始进行搜索,步长为step
def dfs(x,y,step):
    if x == 29 and y == 59: # 搜索到(29,59)
        global ans
        ans = max(ans, step) # 得到最长数字
        return
    for fx,fy in f:
        x_ = x + fx
        y_ = y + fy
        if check(x_,y_):
            step_ = step + int(m[x_][y_])
            if step_ >= record[x_][y_]: # 如果之前的路径没有现在优，那就重新继续搜索，如果现在比之前差，那就不走同样的路径
                record[x_][y_] = step_ 
                dfs(x_,y_,step_)
# 从0,0开始搜索，初始step为m[0][0]
dfs(0,0,int(m[0][0]))
print(record[29][59]) # 得到最后的在(29,59)的最大值

DP方法

m = '''174094882455171152761423221685761892795431233411387427793198
650286024865090061389344606618496378829135984076361542097372
601657541200146071777733599818266038012509478351201640618984
143988087783837107349651099683484992553337438088068198972282
890781586124258626539246182119762952003918195325258677229419
698255491250839396799769357665825441616335532825361862146291
503649293440596342887581257444442930778730382520372975343211
325351222640703400531067500454956482168314849207060705673849
265774579830223671554026061117300483012903885770893074783710
083450145620356667677191627276513995926532444279237315785832
411595106453089134746365281031552217482363035280722591085079
053410485925413958279617719034175332412908745680774313630190
429314820559328748143552689295945058801322270313370955837837
939182801848609300876356583948397645861551964542532682663945
625356614462682551015176002433628234343684739800880514363921
982340231989891351425389287014819359798014755509282450440511
590838726938103384801541373585690893606978941566666714061214
952341523168827712604946036245881214982452998386986623826275
782780208928205527678781609589000725521486468983551558405472
149903035076783644195574734088152324666290493119955560594634
905391288186024902215444250421277955403412298227858394469856
607272647132163832860126054679347881638761723785858733108109
249157334220127702410373959720286708183036202841837581704881
367895556630088230650972282944827258473951902831431040790814
079538232104075905120989173307660289899942087873076421916033
622143260549608274076012938515668898707915863945382394851328
164677964192631597026176253407553188801750590935427267220117
591817866992665840378311257621611574856498432538327068011953
631534031790352912617015229051836886166704989498756486878095
690013558017746707412183571476823027885971347137127534455141'''

m = m.split('\\n')

dp = [[0]*60 for _ in range(30)]


for i in range(30):
    for j in range(60):
        if i == 0 and j== 0:
            dp[i][j] = int(m[i][j])
        elif i == 0:
            dp[i][j] = dp[i][j-1] + int(m[i][j])
        elif j == 0:
            dp[i][j] =dp[i-1][j] + int(m[i][j])
        else:
            dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + int(m[i][j])
print(dp[-1][-1])

✨质数拆分（DFS）

❓️问题描述

将 2022 拆分成不同的质数的和，请问最多拆分成几个?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题不同于质因数分解，是分成不同质数的和，所以简单的想法就是，求出2022中所有的质数，然后从小的数开始组合，看看组合多少个能得到2022。

不过这道题，我仔细想了想，还是要用到DFS，并且我们可以知道，第一个找到的一定是最长的，因为第一个找到的是从最小的开始找，所以这个DFS也就很好写了。

🖥︎参考答案

DFS

可以分成这些质数之和[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 139, 163]，一共有33个

from math import sqrt

# 判断是否是素数
def judge_prime(n):
    if (n == 0 or n == 1): return False
    if (n == 2): return True
    if (n % 2 == 0): return False
    # 判断
    if 0 in [n % i for i in range(2, int(sqrt(n) + 1))]:
        return False
    return True

def equal_prime(n):
    '''n拆分成素数之和'''
    # 首先筛选素数的列表
    plist = [i for i in range(n + 1) if judge_prime(i)]
    DFS(n, 0, 0, plist, S=set())
    
def DFS(n, index=0, sum_num = 0, primes=[], L=[], S=set()):
    if sum_num > n:
        return
    if sum_num == n:
        if (tuple(L) not in S):  # 避免重复输出
            print(L)
            print(sum(L))
            print(len(L))
            exit(-1) # 第一个找到的一定是最大的
            S.add(tuple(L))
        
    # 只要index没有超过素数表primes的长度，就可以继续选择，超过了则不操作，迭代返回上一层
    if (index < len(primes)):
        # sum==n 找到了这样的一组数字
        L.append(primes[index])
        DFS(n, index + 1, sum_num + primes[index], primes, L, S)
        L.pop()
        DFS(n, index + 1, sum_num, primes, L, S)

equal_prime(2022)

✨拷贝时间 (简单计算)

❓️问题描述

小蓝正在拷贝一份文件，他现在已经拷贝了 t秒时间，已经拷贝了 c 字节，文件总共有 s 字节，如果拷贝是匀速进行的，请问小蓝大概还需要拷贝多少秒?

输入格式

输入一行包含三个整数 t,c,s，相邻两个整数之间用一个空格分隔。

输出格式

输出一个整数，表示答案。数据保证答案正好是整数

样例输入

3 10 20

样例输出

样例输入

30 14 21

样例输出

评测用例规模与约定

对于 50%的评测用例，1 <= t, c,s <= 10000。
对于所有评测用例，1<= t,c,s <= 1000000000。

🧠思路

这道题吧，其实也就是简单一道数学题或者说是物理题，首先算出速度 v = c/t，然后(s-c)/t即可得出答案

🖥︎参考代码

t,c,s = map(int,input().split())

v = c / t
print(int((s-c)/v))

✨单词去重 (去重)

❓️问题描述

小蓝有 n 个单词，但是单词中有一些是重复的，请帮小蓝去除重复的单词。

输入格式

输入第一行包含一个正整数 n，表示小蓝的单词数量接下来 n 行，每行包含一个由小写字母组成的单词。
输出格式请输出去除重复后的那些单词。如果一个单词出现了多遍请保留第一次出现的单词，去除之后出现的单词，按输入的顺序输出。

样例输入

5
lanqiao
hi
hello
hello
lanqiao

样例输出

lanqiao
hi
hello

评测用例规模与约定

对于所有评测用例，1<= n <= 100，每个单词的长度不超

🧠思路

实际上，这一部分也就是去重，如果简单的用set的话可以立马解决，但是set是没有顺序的，所以会出现一些问题。

但是后面有一种更妙的想法，我们可以输入单词，然后判断前面有没有出现，如果没有出现就加入列表，否则不加入，最后输出列表即可，顺序就被简单搞定了。

🖥︎参考代码

n = int(input())
words = []
for _ in range(n):
    word = input()
    if word not in words:
        words.append(word)
print('\\n'.join(words))

✨最短回文串（字符串）

❓️问题描述

一个字符串如果从左向右读和从右向左读相同，则称为一个回文串，例如 lanqiaoaiqnal 是一个回文串。小蓝有一个字符串，请将这个字符串右边加上一些字符，使其成为一个回文串。
如果有多种方案，请输出最短的回文串。

输入格式

输入一行包含一个字符串，由小写英文字母组成。

输出格式

输出一行包含答案。

样例输入

lanqiao

样例输出

lanqiaoaiqnal

样例输入

banana

样例输出

bananab

样例输入

noon

样例输出

noon

评测用例规模与约定

对于所有评测用例，1 <= 字符串长度<= 100

🧠思路

首先最简单的想法，就是先判断本身是不是字符串，如果是字符串，那就不用做任何操作

其二就是找到以最后一个字符结尾的最大回文子串，从第二字符开始遍历，如果是就break，因为说吗 $s [i :]$ 是一个回文子串，这样我们只需要在后面加上 $s [: i] [: : - 1]$ 即可

🖥︎参考代码

s = input()

if s == s[::-1]: # 本身就是回文串，打印自己
    print(s) 
else:
    n = len(s)
    for i in range(1,len(s)): # 找到最大字符子串
        if s[i:] == s[i:][::-1]:
            break
    print(s + s[:i][::-1])

✨多少个X？（循环暴力）

❓️问题描述

给定一个字母矩阵。一个 X 图形由中心点和由中心点向四个45度斜线方向引出的直线段组成，四条线段的长度相同，而且四条线段上的字母和中心点的字母相同。
　　一个 X图形可以使用三个整数 r, c, L 来描述，其中 r, c 表示中心点位于第 r 行第 c 列，正整数 L 表示引出的直线段的长度。对于 1 到 L 之间的每个整数 i，X图形满足：第 r-i 行第 c-i 列与第 r 行第 c 列相同，第 r-i 行第 c+i 列与第 r 行第 c 列相同，第 r+i 行第 c-i 列与第 r 行第 c 列相同，第 r+i 行第 c+i 列与第 r 行第 c 列相同。
　　例如，对于下面的字母矩阵中，所有的字母 L 组成一个 X图形，其中中间的 5 个 L 也组成一个 X图形。所有字母 Q 组成了一个 X图形。
　　LAAALA
　　ALQLQA
　　AALQAA
　　ALQLQA
　　LAAALA
　　给定一个字母矩阵，请求其中有多少个 X图形。

输入格式

输入第一行包含两个整数 n, m，分别表示字母矩阵的行数和列数。
　　接下来 n 行，每行 m 个大写字母，为给定的矩阵。

输出格式

输出一行，包含一个整数，表示答案。

样例输入

5 6
LAAALA
ALQLQA
AALQAA
ALQLQA
LAAALA

样例输出

评测用例规模与约定

对于 50% 的评测用例，1 <= n, m <= 10。
对于所有评测用例，1 <= n, m <= 100。

🧠思路

这个模拟题，乍一看，其实很上次求三角形的模拟题也是非常像的，只不过上次找三角形，这次找的是X图形而已，所以思想是一样的，只需要遍历和循环就可以得到答案，直接暴力即可

🖥︎参考代码


n,m = map(int,input().split())

M = []
for _ in range(n):
    M.append(input())

cnt = 0
x = min(n,m)//2 # 最长的长度最大为min(n,m)//2,因为X是对称的
# 可以不遍历最外层一圈，因为单独一个字母不算x图形
for i in range(1,n-1)蓝桥杯第20天（Python）（疯狂刷题第3天）
 蓝桥杯第十四届蓝桥杯模拟赛第三期考场应对攻略（C/C++）
 第十四届蓝桥杯第三期模拟赛 python
 第十四届蓝桥杯第二期模拟赛 python
 第十四届蓝桥杯第二期模拟赛 python
 第十四届蓝桥杯第一期模拟赛 python

蓝桥杯第26天（Python）考前挣扎

题型：

模板回顾： 1.DFS代码框架（搜图建议↓为x方向，→为y方向）（找有多少条路径）

搜路径模板

搜索组合模板

BFS+DFS

2.BFS逐层搜索（找最短路径）

搜索模板

BFS搜索示例 （通过set（）去重）

3.并查集（连通子图，最小生成树）

4.DP动态规划 （ 完全背包 http://t.csdn.cn/HnkGN）（ http://t.csdn.cn/jSSby）

0/1背包问题：

最长公共子序列

最长递增子序列（LIS）

编辑距离（字符串转换）

5.数论

LCM和GCD

快速幂

矩阵乘法

埃式筛

大数分解（质因数分解）

6.组合数学

加法原理

鸽巢原理

杨辉三角

7.计算几何

点积

叉积

点跟直线关系

8.图论算法（图论章节http://t.csdn.cn/pitI6）

存边方式

Floyd算法

Dijstra算法

Bellman-ford算法

9.常用库

10.前缀和、差分

第十四届蓝桥杯第二期模拟赛 python

第十四届蓝桥杯第二期模拟赛 【python】

文章目录

✨最小的2022 (python二进制)

❓️问题描述

答案提交

🧠思路

🖥︎参考答案

✨经过天数（datetime库）

❓️问题描述

答案提交

🧠思路

🖥︎参考答案

✨特殊的十六进制数 （int16进制）

❓️问题描述

答案提交

🧠思路

🖥︎参考答案

✨矩阵的最小路径 （DP/DFS)

❓️问题描述

答案提交

🧠思路

🖥︎参考答案

DFS方法

DP方法

✨质数拆分 （DFS）

❓️问题描述

答案提交

🧠思路

🖥︎参考答案

DFS

✨拷贝时间 (简单计算)

❓️问题描述

输入格式

输出格式

样例输入

样例输出

样例输入

样例输出

评测用例规模与约定

🧠思路

🖥︎参考代码

✨单词去重 (去重)

❓️问题描述

模板回顾：
1.DFS代码框架（搜图建议↓为x方向，→为y方向）（找有多少条路径）

BFS搜索示例（通过set（）去重）

4.DP动态规划（完全背包 http://t.csdn.cn/HnkGN）（ http://t.csdn.cn/jSSby）

第十四届蓝桥杯第二期模拟赛【python】

✨特殊的十六进制数（int16进制）

✨矩阵的最小路径（DP/DFS)

✨质数拆分（DFS）

✨最短回文串（字符串）

✨多少个X？（循环暴力）