BFS广度优先搜索之钥匙和房间

Posted 2023-04-07 风老魔

841. 钥匙和房间

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。

当你进入一个房间，你可能会在里面找到一套不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。

给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true，否则返回 false。

示例 1：

输入：rooms = [[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。
示例 2：

输入：rooms = [[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。

提示：

n == rooms.length
2 <= n <= 1000
0 <= rooms[i].length <= 1000
1 <= sum(rooms[i].length) <= 3000
0 <= rooms[i][j] < n
所有 rooms[i] 的值 互不相同

题解：

class Solution:
    def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
        visited = 0	# 记录已经穷举过的钥匙，防止走回头路
        queue = [0]

        while queue:
            index_keys = queue.pop()
            for i in rooms[index_keys]:
                if i not in visited:
                    visited.add(i)
                    queue.insert(0, i)

        return len(visited) == len(rooms)

这个题还可以用 DFS，只需将 queue.insert 换成 queue.append 即可

参考：7行DFS 8行BFS 两种方法 三种实现 超详细趣味０基础解 Python

算法之深度和广度优先搜索算法

什么是“搜索”算法？

图上的搜索算法，最直接的理解就是，在图中找出从一个顶点出发，到另一个顶点的路径。具体方法有很多，比如今天要讲的两种最简单、最“暴力”的深度优先、广度优先搜索。

广度优先搜索（BFS）

广度优先搜索（Breadth-First-Search），我们平常都把简称为 BFS。直观地讲，它其实就是一种“地毯式”层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近的，依次往外搜索。

bfs() 函数就是基于之前定义的，图的广度优先搜索的代码实现。其中 s 表示起始顶点，t 表示终止顶点。我们搜索一条从 s 到 t 的路径。实际上，这样求得的路径就是从 s到 t 的最短路径。

无向图代码：

广度优先搜索算法代码：

public void bfs(int s, int t) { if (s == t) return; boolean[] visited = new boolean[v]; visited[s]=true; Queue<Integer> queue = new LinkedList<>(); queue.add(s); int[] prev = new int[v]; for (int i = 0; i < v; ++i) { prev[i] = -1; } while (queue.size() != 0) { int w = queue.poll(); for (int i = 0; i < adj[w].size(); ++i) { int q = adj[w].get(i); if (!visited[q]) { prev[q] = w; if (q == t) { print(prev, s, t); return; } visited[q] = true; queue.add(q); } } }} private void print(int[] prev, int s, int t) { // 递归打印 s->t 的路径 if (prev[t] != -1 && t != s) { print(prev, s, prev[t]); } System.out.print(t + " ");}

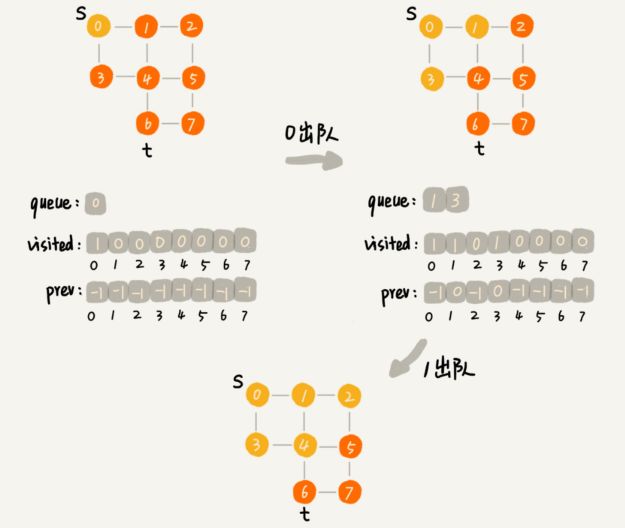
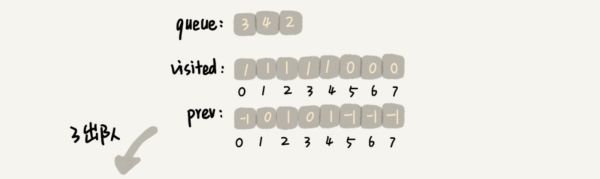
visited是用来记录已经被访问的顶点，用来避免顶点被重复访问。如果顶点 q 被访问，那相应的 visited[q] 会被设置为 true。

queue是一个队列，用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的，也就是说，我们只有把第 k 层的顶点都访问完成之后，才能访问第 k+1 层的顶点。当我们访问到第 k 层的顶点的时候，我们需要把第 k 层的顶点记录下来，稍后才能通过第 k 层的顶点来找第 k+1 层的顶点。所以，我们用这个队列来实现记录的功能。

prev用来记录搜索路径。当我们从顶点 s 开始，广度优先搜索到顶点 t 后，prev 数组中存储的就是搜索的路径。不过，这个路径是反向存储的。prev[w] 存储的是，顶点 w 是从哪个前驱顶点遍历过来的。比如，我们通过顶点 2 的邻接表访问到顶点 3，那 prev[3] 就等于 2。为了正向打印出路径，我们需要递归地来打印，你可以看下 print() 函数的实现方式。

深度优先搜索（DFS）

深度优先搜索（Depth-First-Search），简称 DFS。最直观的例子就是“走迷宫”。假设你站在迷宫的某个岔路口，然后想找到出口。你随意选择一个岔路口来走，走着走着发现走不通的时候，你就回退到上一个岔路口，重新选择一条路继续走，直到最终找到出口。这种走法就是一种深度优先搜索策略

搜索的起始顶点是 s，终止顶点是 t，我们希望在图中寻找一条从顶点 s 到顶点 t 的路径。如果映射到迷宫那个例子，s 就是你起始所在的位置，t 就是出口。

用深度递归算法，把整个搜索的路径标记出来了。这里面实线箭头表示遍历，虚线箭头表示回退。从图中我们可以看出，深度优先搜索找出来的路径，并不是顶点 s 到顶点 t 的最短路径。

实际上，深度优先搜索用的是一种比较著名的算法思想，回溯思想。这种思想解决问题的过程，非常适合用递归来实现。

我把上面的过程用递归来翻译出来，就是下面这个样子。可以发现，深度优先搜索代码实现也用到了 prev、visited 变量以及 print() 函数，它们跟广度优先搜索代码实现里的作用是一样的。不过，深度优先搜索代码实现里，有个比较特殊的变量 found，它的作用是，当我们已经找到终止顶点 t 之后，我们就不再递归地继续查找了。

 boolean found = false; // 全局变量或者类成员变量 public void dfs(int s, int t) { found = false; boolean[] visited = new boolean[v]; int[] prev = new int[v]; for (int i = 0; i < v; ++i) { prev[i] = -1; } recurDfs(s, t, visited, prev); print(prev, s, t);}  private void recurDfs(int w, int t, boolean[] visited, int[] prev) { if (found == true) return; visited[w] = true; if (w == t) { found = true;          return;}for (int i = 0; i < adj[w].size(); ++i) {    if (found == true) return;  int q = adj[w].get(i); if (!visited[q]) { prev[q] = w; recurDfs(q, t, visited, prev); } }}

参考网站：

https://blog.csdn.net/raphealguo/article/details/7523411