走遍无人区之深度优先搜索（DFS）和广度优先搜索（BFS）

Posted 2021-07-02 重返无人区

     通过深度优先搜索算法思想探索无人区中的道路，虽然速度很快，但是当在无人区中面临缺水的情况下，大家是不是都会叫苦连天呢？哇！还有好远的路啊！都没有水喝了！！为了能够够尽快的到达目的地，这时我们就需要另一位好兄弟——广度优先搜索算法光荣登场啦！

     二、广度优先搜索算法( Breadth First Search ，BSF)

    与深度优先搜索算法相比，广度优先搜索算法则可以理解成一名做事踏实稳重、循规蹈矩的中年人，从而我们可以知道广度优先搜索算法的搜索范围之广，虽然最终能够获得最优解，但往往搜索过程较漫长，消耗时间也比较长，因此广度优先搜索算法也被称为盲目搜索算法。其搜索过程可如下图所示：

    因此，广度优先搜索算法的计算思想可以通俗的理解为：当我们在起始路口“0”时，发现有两条路可以帮助我们分别到达“1”路口和“2”路口。我们首先会选择上面一条路到达路口“1”，但此时依照现在的做事风格，我们则不会继续通过路口“1”探索到达路口“3”，而是返回到起始路口“0”，通过另一条路对路口“2”进行探索。此时，当距离起始路口“1”最近的两个路口“1”和“2”被探索完成之后，我们又从最初探索的路口“1”开始，继续探索通过路口“1”能够到达的路口。而我们发现在路口“1” 处只有一条路供我们选择，并且通过这一条路帮助我们完成对路口“3”的探索。此时，路口“1”的通路都已经探索完成，同样我们没有从路口“3”开始继续向下探索，而是回到路口“2”对其进行探索，然而当我们发现路口“2”处没有路可以让我们继续走下去的时候，我们则回到刚刚探索过的路口“3”，继续探索从路口“3”可以到达的所有路口，从而可以发现通过路口“3” 我们可以顺利到达路口“4”和路口“2”，此时我们便可得到到达终点的最短路径啦！

     当然，同好兄弟深度优先搜索算法一样，为了避免走重复的路，因此我们将已经走过的路口单独进行记忆，在下一次遇到时大脑就会迅速判断出“哦豁！这个路口已经走过了！”，所以我们就会继续选择那些没有走过的节点进行探索，直到探索到我们期望前往的终点。

     现在让我们从实例中回归到原理本身，广度优先搜索算法的树状结构原理解释可以总结如下所示：

    依据前面的讨论，使用广度优先搜索算法实现上述树状结构排序的代码结构如下所示：

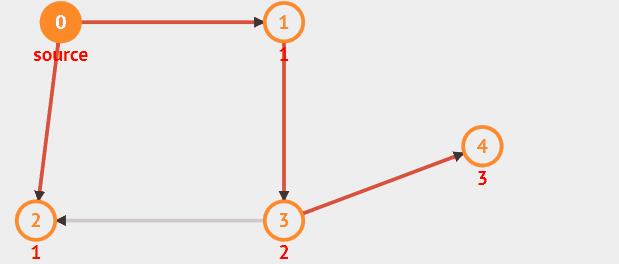
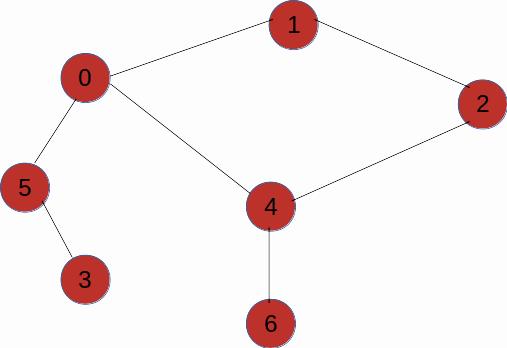
# -*- coding: utf-8 -*-
from collections import deque # 线性表的模块

# 首先定义一个创建图的类，使用邻接矩阵class Graph(object): def __init__(self, *args, **kwargs): self.order = [] # visited order self.neighbor = {}
 def add_node(self, node): key, val = node if not isinstance(val, list): print('节点输入时应该为一个线性表') # 避免不正确的输入 self.neighbor[key] = val
 # 广度优先算法的实现 def BFS(self, root): # 首先判断根节点是否为空节点 if root != None: search_queue = deque() search_queue.append(root) visited = [] else: print('root is None') return -1
 while search_queue: person = search_queue.popleft() #self.order.append(person) if person in self.order: continue else: self.order.append(person)
 if (not person in visited) and (person in self.neighbor.keys()): search_queue += self.neighbor[person] visited.append(person)

 def node_print(self): for index in self.order: print(index, end=' ')

if __name__ == '__main__': # 创建一个树状结构 g = Graph() g.add_node(('1', ['0', '2'])) g.add_node(('0', ['5', '4'])) g.add_node(('5', ['3'])) g.add_node(('4', ['6'])) g.add_node(('2', ['4']))


 # 进行广度优先搜索 g.BFS('1') print('广度优先搜索:') print(' ', end=' ') g.node_print()

    上述代码的运算结果如下所示：

广度优先搜索: 1 0 2 5 4 3 6

    如何探索出一条最优路径，想必各位小伙伴也已经Get到了其中的思想精髓，是不是再也不怕在探索过程中没有水喝了呢，赶快动身继续前进吧！当然，在深度优先搜索和广度优先搜索算法这对好兄弟当中还蕴含着许许多多小思想、小方法，我们也将在后续逐渐详细介绍到。接下来，我们将得到前面几位兄弟的帮助，正是打开路径规划的探索之路啦!