Transformer架构:位置编码
Posted Jayson13
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Transformer架构:位置编码相关的知识,希望对你有一定的参考价值。
2017年,Google的Vaswani 等人提出了一种新颖的纯注意力序列到序列架构,闻名学术界与工业界的 Transformer 架构横空出世。它的可并行化训练能力和优越的性能使其成为自然语言处理领域(Natural Language Processing,NLP)以及计算机视觉领域(Computer Vision,CV)研究人员的热门选择。本文将重点讨论Transformer架构一个不可或缺的部分——位置编码(Positional Encoding)。
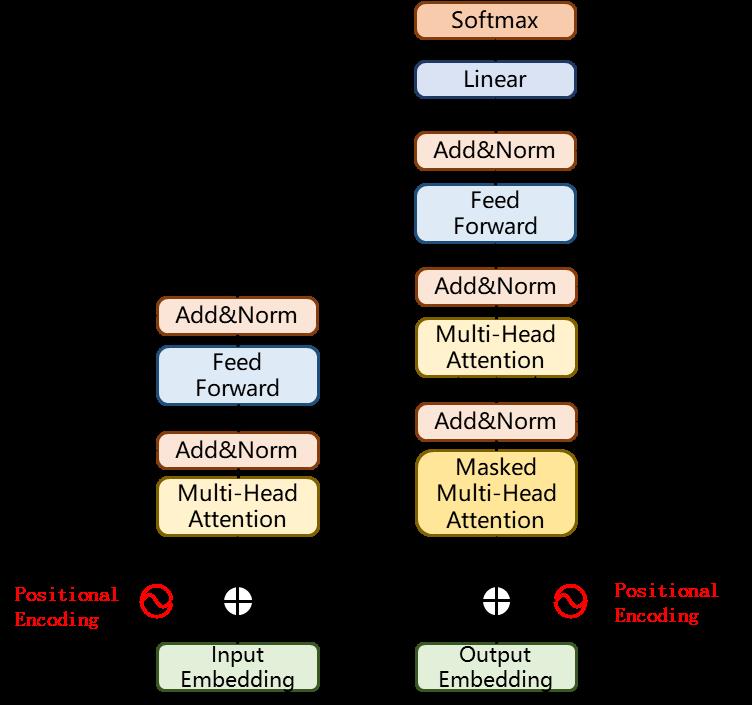
位置编码是什么?它为什么这么重要?
在人类的语言中,单词的位置与顺序定义了语法,也影响着语义。无法捕获的单词顺序会导致我们很难理解一句话的含义,如下图所示。

因此在NLP任务中,对于任何神经网络架构,能够有效识别每个词的位置与词之间的顺序是十分关键的。传统的循环神经网络(RNN)本身通过自回归的方式考虑了单词之间的顺序。然而Transformer 架构不同于RNN,Transformer 使用纯粹的自注意力机制来捕获词之间的联系。纯粹的自注意力机制具有置换不变的性质(证明请见)。换句话说,Transformer中的自注意力机制无法捕捉输入元素序列的顺序。因此我们需要一种方法将单词的顺序合并到Transformer架构中,于是位置编码应运而生。

位置编码的作用方式
目前,主流的位置编码方法主要分为绝对位置编码与相对位置编码两大类。其中绝对位置编码的作用方式是告知Transformer架构每个元素在输入序列的位置,类似于为输入序列的每个元素打一个"位置标签"标明其绝对位置。而相对位置编码作用于自注意力机制,告知Transformer架构两两元素之间的距离。如下图所示。

绝对位置编码
最早的绝对位置编码起源于2017年Jonas Gehring等人发表的Convolutional Sequence to Sequence Learning,该工作使用可训练的嵌入形式作为位置编码。随后Google的Vaswani等人在Attention Is All You Need文章中使用正余弦函数生成的位置编码。关于Transformer架构为什么选择正余弦函数去生成绝对位置编码以及正余弦函数的一些特性,笔者安利大家阅读kazemnejad老师的博文《Transformer Architecture: The Positional Encoding》,该文详细叙述了正余弦绝对位置编码的原理。诞生于 2018 年末的 BERT也采用了可训练的嵌入形式作为编码。实际上,这三项工作的共性都是在每个词的嵌入上加位置编码之后输入模型。形式上,如下公式所示:
x
=
(
w
1
+
p
1
,
.
.
.
,
w
m
+
p
m
)
.
x = (w_1 + p_1, . . . ,w_m + p_m).
x=(w1+p1,...,wm+pm).
其中,
x
x
x表示模型的输入,
w
m
w_m
wm表示第
m
m
m个位置的词嵌入,
p
m
p_m
pm表示第
m
m
m个位置的绝对位置编码。
近年来,关于绝对位置编码的工作大多数是以不同的方法生成绝对位置编码为主。下面列出一些关于绝对位置编码的一些工作,感兴趣的同学可以了解一下~
- Learning to Encode Position for Transformer with Continuous Dynamical Model
该文提出一种基于连续动态系统的绝对位置编码(FLOATER),从数据中学习神经微分方程递归生成位置编码,在机器翻译、自然语言理解和问答等任务上获得了不错的性能提升。
由于递归机制本身具有出色的外推性质,所以FLOATER基本不受文本长度的限制。并且作者说明了正余弦绝对位置编码就是FLOATER的一个特解。该工作在WMT14 En-De和En-Fr分别进行了实验,分别对比Transformer Base模型有着0.4和1.0 BLEU值的涨幅。但与此同时,这种递归形式的位置编码也牺牲了原本模型的并行输入,在速度上会有一定影响。 - Encoding Word Order in Complex Embeddings
该工作提出一种复值词向量函数生成绝对位置编码,巧妙地将复值函数的振幅和相位与词义和位置相联系,在机器翻译、文本分类和语言模型任务上获得了不错的性能提升。。
该复值词向量函数以位置为变量,计算每个词在不同位置的词向量。由于该函数对于位置变量而言是连续的,因此该方法不光建模了绝对位置,也建模了词之间的相对位置。该工作在WMT16 En-De机器翻译任务数据集上进行了实验,复值词向量对比Transformer Base模型有1.3 BLEU值的涨幅。 - SHAPE: Shifted Absolute Position Embedding for Transformers
该工作提出了一种绝对位置编码的鲁棒性训练方法。作者认为现有的位置编码方法在测试不可见长度时缺乏泛化能力,并提出了平移绝对位置编码(SHAPE)来解决这两个问题。SHAPE的基本思想是在训练过程中对绝对位置编码随机整体平移一段距离来实现泛化能力。该工作在WMT16 En-De机器翻译任务数据集上进行训练,将newstest2010-2016作为校验集和测试集,对比正余弦绝对位置编码,该方法有着一定的性能提升。
相对位置编码
最经典的相对位置编码起源于Shaw等人发表的Self-Attention with Relative Position Representations。在介绍相对位置表示之前,首先简要介绍一下自注意力机制的计算流程,对于Transformer模型的某一自注意力子层: 声明: 在接下来的架构分析中, 我们将假设使用Transformer模型架构处理从一种语言文本到另一种语言文本的翻译工作, 因此很多命名方式遵循NLP中的规则. 比如: Embeddding层将称作文本嵌入层, Embedding层产生的张量称为词嵌入张量, 它的最后一维将称作词向量等. Transformer总体架构可分为四个部分: 输入部分包含: 输入部分包含: 无论是源文本嵌入还是目标文本嵌入,都是为了将文本中词汇的数字表示转变为向量表示, 希望在这样的高维空间捕捉词汇间的关系. pytorch 0.3.0及其必备工具包的安装: 文本嵌入层的代码分析: nn.Embedding演示: 实例化参数: 输入参数: 调用: 输出效果: 因为在Transformer的编码器结构中, 并没有针对词汇位置信息的处理,因此需要在Embedding层后加入位置编码器,将词汇位置不同可能会产生不同语义的信息加入到词嵌入张量中, 以弥补位置信息的缺失. nn.Dropout演示: torch.unsqueeze演示: 实例化参数: 输入参数: 调用: 输出效果: 绘制词汇向量中特征的分布曲线: 输出效果: 加油! 感谢! 努力!
Q
=
x
W
Q
K
=
x
W
K
V
=
x
W
V
Q= x W_Q \\\\ K=xW_K \\\\ V=xW_V
Q=xWQK=xWKV=xWV
其中,
x
x
x为上一层的输出,
W
Q
W_Q
WQ、
W
K
W_K
WK、
W
V
W_V
WV为模型参数,它们可以通过自动学习得到。此时,对于整个模型输入的向量序列
x
=
x
1
,
…
,
x
m
x=\\x_1,\\ldots,x_m\\
x=x1,…,xm,通过点乘计算,可以得到当前位置
i
i
i和序列中所有位置间的关系,记为
z
i
z_i
zi,计算公式如下:
z
i
=
∑
j
=
1
m
α
i
j
(
x
j
W
V
)
z_i = \\sum_j=1^m \\alpha_ij(x_j W_V)
zi=j=1∑mαij(xjWV)
这里,
z
i
z_i
zi可以被看做是输入序列的线性加权表示结果。而权重
α
i
j
\\alpha_ij
αij通过Softmax函数得到:
α
i
j
=
exp
(
e
i
j
)
∑
k
=
1
m
exp
(
e
i
k
)
\\alpha_ij = \\frac\\exp (e_ij)\\sum_k=1^m\\exp (e_ik)
αij=∑k=1mexp(eik)exp(eij)
进一步,
e
i
j
e_ij
eij被定义为:
e
i
j
=
(
x
i
W
Q
)
(
x
j
W
K
)
T
d
k
e_ij = \\frac(x_i W_Q)(x_j W_K)^\\textrmT\\sqrtd_k
eij=dk(xiWQ)(xjWK)T
其中,
d
k
d_k
dk为模型中隐藏层的维度。
e
i
j
e_ij
eij实际上就是
Q
Q
Q和
K
K
K的向量积缩放后的一个结果。而相对位置表示的核心思想就是在
z
i
z_i
zi与
e
i
j
e_ij
eij的计算公式里面分别引入了可学习的相对位置向量
a
i
j
V
a_ij^V
aijV与
a
i
j
K
a_ij^K
aijK。改进后的自注意力机制如下:
z
i
=
∑
j
=
1
m
α
i
j
(
x
j
W
V
+
a
i
j
V
)
e
i
j
=
x
i
W
Q
(
x
j
W
K
+
a
i
j
K
)
T
d
k
=
x
i
W
Q
(
x
j
W
K
)
T
+
x
i
W
Q
(
a
i
j
K
)
T
d
k
\\beginaligned z_i &= \\sum_j=1^m \\alpha_ij(x_j W_V +a_ij^V) \\\\ e_ij &= \\fracx_i W_Q(x_j W_K +a_ij^K )^\\textrmT\\sqrtd_k\\\\ &= \\fracx_i W_Q(x_j W_K)^\\textrmT +x_iW_Q(a_ij^K )^T\\sqrtd_k \\endaligned
zieij
【NLP】Transformer架构解析
1. 认识Transformer架构
1.1 Transformer模型的作用
1.2 Transformer总体架构图


输出部分包含:
编码器部分: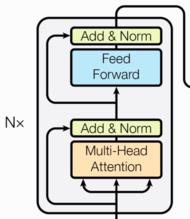
解码器部分:
2. 输入部分实现

2.1 文本嵌入层的作用
# 使用pip安装的工具包包括pytorch-0.3.0, numpy, matplotlib, seaborn
pip install http://download.pytorch.org/whl/cu80/torch-0.3.0.post4-cp36-cp36m-linux_x86_64.whl numpy matplotlib seaborn
# MAC系统安装, python版本<=3.6
pip install torch==0.3.0.post4 numpy matplotlib seaborn
# 导入必备的工具包
import torch
# 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层,
# 比如,卷积层, lstm层, embedding层等, 不需要我们再重新造轮子.
import torch.nn as nn
# 数学计算工具包
import math
# torch中变量封装函数Variable.
from torch.autograd import Variable
# 定义Embeddings类来实现文本嵌入层,这里s说明代表两个一模一样的嵌入层, 他们共享参数.
# 该类继承nn.Module, 这样就有标准层的一些功能, 这里我们也可以理解为一种模式, 我们自己实现的所有层都会这样去写.
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
"""类的初始化函数, 有两个参数, d_model: 指词嵌入的维度, vocab: 指词表的大小."""
# 接着就是使用super的方式指明继承nn.Module的初始化函数, 我们自己实现的所有层都会这样去写.
super(Embeddings, self).__init__()
# 之后就是调用nn中的预定义层Embedding, 获得一个词嵌入对象self.lut
self.lut = nn.Embedding(vocab, d_model)
# 最后就是将d_model传入类中
self.d_model = d_model
def forward(self, x):
"""可以将其理解为该层的前向传播逻辑,所有层中都会有此函数
当传给该类的实例化对象参数时, 自动调用该类函数
参数x: 因为Embedding层是首层, 所以代表输入给模型的文本通过词汇映射后的张量"""
# 将x传给self.lut并与根号下self.d_model相乘作为结果返回
return self.lut(x) * math.sqrt(self.d_model)
>>> embedding = nn.Embedding(10, 3)
>>> input = torch.LongTensor([[1,2,4,5],[4,3,2,9]])
>>> embedding(input)
tensor([[[-0.0251, -1.6902, 0.7172],
[-0.6431, 0.0748, 0.6969],
[ 1.4970, 1.3448, -0.9685],
[-0.3677, -2.7265, -0.1685]],
[[ 1.4970, 1.3448, -0.9685],
[ 0.4362, -0.4004, 0.9400],
[-0.6431, 0.0748, 0.6969],
[ 0.9124, -2.3616, 1.1151]]])
>>> embedding = nn.Embedding(10, 3, padding_idx=0)
>>> input = torch.LongTensor([[0,2,0,5]])
>>> embedding(input)
tensor([[[ 0.0000, 0.0000, 0.0000],
[ 0.1535, -2.0309, 0.9315],
[ 0.0000, 0.0000, 0.0000],
[-0.1655, 0.9897, 0.0635]]])
# 词嵌入维度是512维
d_model = 512
# 词表大小是1000
vocab = 1000
# 输入x是一个使用Variable封装的长整型张量, 形状是2 x 4
x = Variable(torch.LongTensor([[100,2,421,508],[491,998,1,221]]))
emb = Embeddings(d_model, vocab)
embr = emb(x)
print("embr:", embr)
embr: Variable containing:
( 0 ,.,.) =
35.9321 3.2582 -17.7301 ... 3.4109 13.8832 39.0272
8.5410 -3.5790 -12.0460 ... 40.1880 36.6009 34.7141
-17.0650 -1.8705 -20.1807 ... -12.5556 -34.0739 35.6536
20.6105 4.4314 14.9912 ... -0.1342 -9.9270 28.6771
( 1 ,.,.) =
27.7016 16.7183 46.6900 ... 17.9840 17.2525 -3.9709
3.0645 -5.5105 10.8802 ... -13.0069 30.8834 -38.3209
33.1378 -32.1435 -3.9369 ... 15.6094 -29.7063 40.1361
-31.5056 3.3648 1.4726 ... 2.8047 -9.6514 -23.4909
[torch.FloatTensor of size 2x4x512]
2.2 位置编码器的作用
# 定义位置编码器类, 我们同样把它看做一个层, 因此会继承nn.Module
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
"""位置编码器类的初始化函数, 共有三个参数, 分别是d_model: 词嵌入维度,
dropout: 置0比率, max_len: 每个句子的最大长度"""
super(PositionalEncoding, self).__init__()
# 实例化nn中预定义的Dropout层, 并将dropout传入其中, 获得对象self.dropout
self.dropout = nn.Dropout(p=dropout)
# 初始化一个位置编码矩阵, 它是一个0阵,矩阵的大小是max_len x d_model.
pe = torch.zeros(max_len, d_model)
# 初始化一个绝对位置矩阵, 在我们这里,词汇的绝对位置就是用它的索引去表示.
# 所以我们首先使用arange方法获得一个连续自然数向量,然后再使用unsqueeze方法拓展向量维度使其成为矩阵,
# 又因为参数传的是1,代表矩阵拓展的位置,会使向量变成一个max_len x 1 的矩阵,
position = torch.arange(0, max_len).unsqueeze(1)
# 绝对位置矩阵初始化之后,接下来就是考虑如何将这些位置信息加入到位置编码矩阵中,
# 最简单思路就是先将max_len x 1的绝对位置矩阵, 变换成max_len x d_model形状,然后覆盖原来的初始位置编码矩阵即可,
# 要做这种矩阵变换,就需要一个1xd_model形状的变换矩阵div_term,我们对这个变换矩阵的要求除了形状外,
# 还希望它能够将自然数的绝对位置编码缩放成足够小的数字,有助于在之后的梯度下降过程中更快的收敛. 这样我们就可以开始初始化这个变换矩阵了.
# 首先使用arange获得一个自然数矩阵, 但是细心的同学们会发现, 我们这里并没有按照预计的一样初始化一个1xd_model的矩阵,
# 而是有了一个跳跃,只初始化了一半即1xd_model/2 的矩阵。 为什么是一半呢,其实这里并不是真正意义上的初始化了一半的矩阵,
# 我们可以把它看作是初始化了两次,而每次初始化的变换矩阵会做不同的处理,第一次初始化的变换矩阵分布在正弦波上, 第二次初始化的变换矩阵分布在余弦波上,
# 并把这两个矩阵分别填充在位置编码矩阵的偶数和奇数位置上,组成最终的位置编码矩阵.
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
# 这样我们就得到了位置编码矩阵pe, pe现在还只是一个二维矩阵,要想和embedding的输出(一个三维张量)相加,
# 就必须拓展一个维度,所以这里使用unsqueeze拓展维度.
pe = pe.unsqueeze(0)
# 最后把pe位置编码矩阵注册成模型的buffer,什么是buffer呢,
# 我们把它认为是对模型效果有帮助的,但是却不是模型结构中超参数或者参数,不需要随着优化步骤进行更新的增益对象.
# 注册之后我们就可以在模型保存后重加载时和模型结构与参数一同被加载.
self.register_buffer('pe', pe)
def forward(self, x):
"""forward函数的参数是x, 表示文本序列的词嵌入表示"""
# 在相加之前我们对pe做一些适配工作, 将这个三维张量的第二维也就是句子最大长度的那一维将切片到与输入的x的第二维相同即x.size(1),
# 因为我们默认max_len为5000一般来讲实在太大了,很难有一条句子包含5000个词汇,所以要进行与输入张量的适配.
# 最后使用Variable进行封装,使其与x的样式相同,但是它是不需要进行梯度求解的,因此把requires_grad设置成false.
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
# 最后使用self.dropout对象进行'丢弃'操作, 并返回结果.
return self.dropout(x)
>>> m = nn.Dropout(p=0.2)
>>> input = torch.randn(4, 5)
>>> output = m(input)
>>> output
Variable containing:
0.0000 -0.5856 -1.4094 0.0000 -1.0290
2.0591 -1.3400 -1.7247 -0.9885 0.1286
0.5099 1.3715 0.0000 2.2079 -0.5497
-0.0000 -0.7839 -1.2434 -0.1222 1.2815
[torch.FloatTensor of size 4x5]
>>> x = torch.tensor([1, 2, 3, 4])
>>> torch.unsqueeze(x, 0)
tensor([[ 1, 2, 3, 4]])
>>> torch.unsqueeze(x, 1)
tensor([[ 1],
[ 2],
[ 3],
[ 4]])
# 词嵌入维度是512维
d_model = 512
# 置0比率为0.1
dropout = 0.1
# 句子最大长度
max_len=60
# 输入x是Embedding层的输出的张量, 形状是2 x 4 x 512
x = embr
Variable containing:
( 0 ,.,.) =
35.9321 3.2582 -17.7301 ... 3.4109 13.8832 39.0272
8.5410 -3.5790 -12.0460 ... 40.1880 36.6009 34.7141
-17.0650 -1.8705 -20.1807 ... -12.5556 -34.0739 35.6536
20.6105 4.4314 14.9912 ... -0.1342 -9.9270 28.6771
( 1 ,.,.) =
27.7016 16.7183 46.6900 ... 17.9840 17.2525 -3.9709
3.0645 -5.5105 10.8802 ... -13.0069 30.8834 -38.3209
33.1378 -32.1435 -3.9369 ... 15.6094 -29.7063 40.1361
-31.5056 3.3648 1.4726 ... 2.8047 -9.6514 -23.4909
[torch.FloatTensor of size 2x4x512]
pe = PositionalEncoding(d_model, dropout, max_len)
pe_result = pe(x)
print("pe_result:", pe_result)
pe_result: Variable containing:
( 0 ,.,.) =
-19.7050 0.0000 0.0000 ... -11.7557 -0.0000 23.4553
-1.4668 -62.2510 -2.4012 ... 66.5860 -24.4578 -37.7469
9.8642 -41.6497 -11.4968 ... -21.1293 -42.0945 50.7943
0.0000 34.1785 -33.0712 ... 48.5520 3.2540 54.1348
( 1 ,.,.) =
7.7598 -21.0359 15.0595 ... -35.6061 -0.0000 4.1772
-38.7230 8.6578 34.2935 ... -43.3556 26.6052 4.3084
24.6962 37.3626 -26.9271 ... 49.8989 0.0000 44.9158
-28.8435 -48.5963 -0.9892 ... -52.5447 -4.1475 -3.0450
[torch.FloatTensor of size 2x4x512]
import matplotlib.pyplot as plt
# 创建一张15 x 5大小的画布
plt.figure(figsize=(15, 5))
# 实例化PositionalEncoding类得到pe对象, 输入参数是20和0
pe = PositionalEncoding(20, 0)
# 然后向pe传入被Variable封装的tensor, 这样pe会直接执行forward函数,
# 且这个tensor里的数值都是0, 被处理后相当于位置编码张量
y = pe(Variable(torch.zeros(1, 100, 20)))
# 然后定义画布的横纵坐标, 横坐标到100的长度, 纵坐标是某一个词汇中的某维特征在不同长度下对应的值
# 因为总共有20维之多, 我们这里只查看4,5,6,7维的值.
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
# 在画布上填写维度提示信息
plt.legend(["dim %d"%p for p in [4,5,6,7]])

效果分析: