机器学习-卷积神经网络CNN中的单通道和多通道图片差异

Posted 2023-03-29 Gaosiy

背景

最近在使用CNN的场景中，既有单通道的图片输入需求，也有多通道的图片输入需求，因此又整理回顾了一下单通道或者多通道卷积的差别，这里记录一下探索过程。

结论

直接给出结论，单通道图片和多通道图片在经历了第一个卷积层以后，就没有单通道或者多通道的区别了，剩下的网络可以采取完全一样的结构。这也为我们使用各种各样的网络架构，resnet，Alexnet，vgg提供了方便，因为他们都是为了跑ImageNet而设计的特定输入。

图解

1.成员介绍

在CNN中涉及到的主要就是image kernel bias这三个元素。这里image表示是首层的输入，后边卷积层的impute都是前边的output，与首层操作类似，不再多说。

2.单通道图片卷积过程

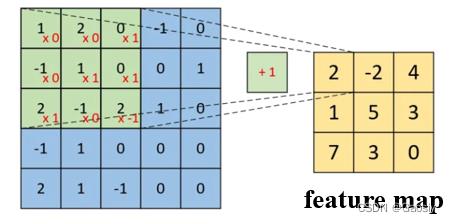
可以看到，通过对应位置相乘再相加，结合bias，最终得到feature map中的一个元素，所以卷积核的一次计算只得到一个数。当卷积核刷遍整张图片以后，得到了一个完整的feature map。这个东西将作为下一层的输入，传递下去。

通常来说，我们的卷积层不会只有一个kernel，因为一个kernel只能提取图片的一类特征，我们使用CNN的目的就在于应用多个kernel学习到多个特征，下面给出使用两个kernel的例子。

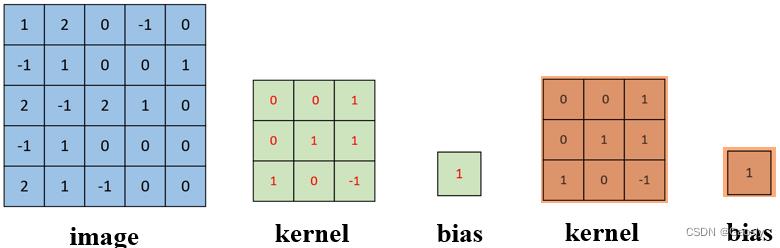
每一个kernel都会来一遍上图中获得feature map的过程。最终我们会得到2个feature map，与卷积核的数量一致。

2.RGB三通道图片卷积过程

 

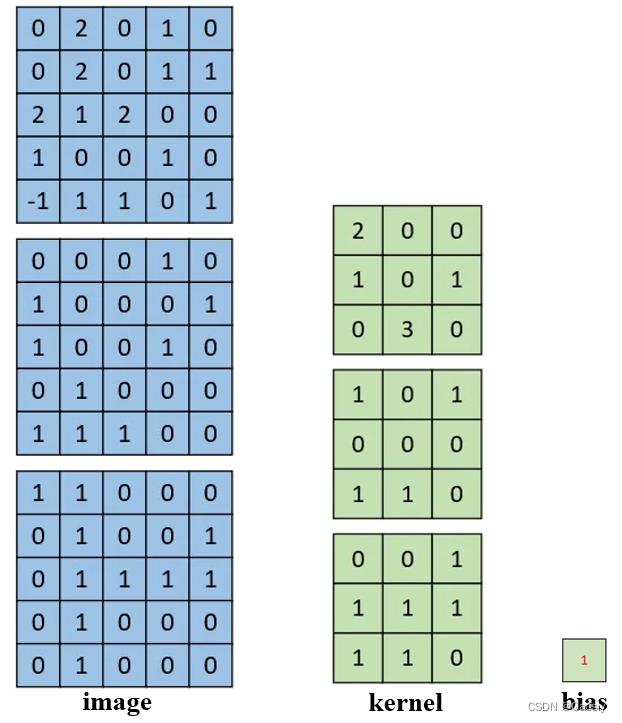
这里可以看到，图片从一个矩阵变为了3个，这时候kernel也变成了3个矩阵，请注意 ，这三个叫做一个kernel，但是这三个kernel共享一个bias。在卷积运算的时候，这个kernel的三个通道分别与对应的图片通道做卷积，过程与单通道处理是一样的，但是这里由于有三个通道，所以会得到3个数字，而不是之前的一个数字，但是这里的三个数字会直接相加，最终还是一个数字，所以这里就是3通道卷积的trick所在，这里是容易疑惑的一个点，搞明白就好。

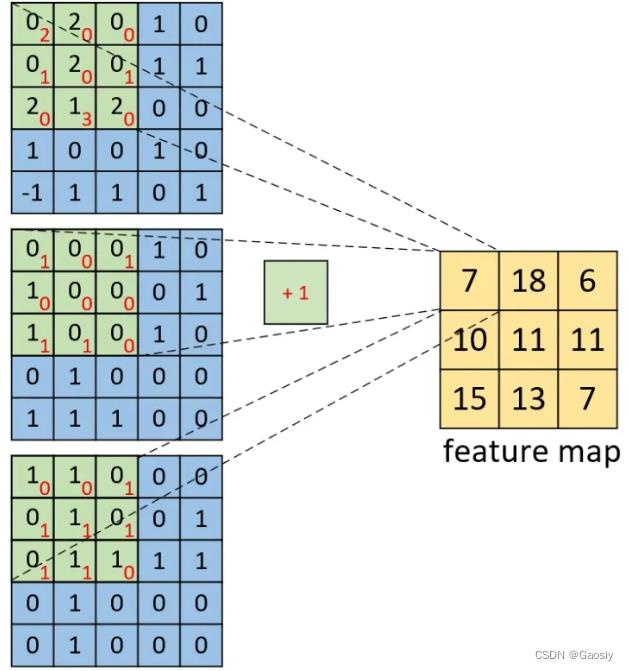
多个kernel可以类比之前的单通道，总之，结论就是，不管是单通道还是三通道的首个卷积层，都会输出与kernel数量相等的feature map。且不管是不是单通道，只要图片宽高是一样的，单通道和多通道的首个卷积层过后，得到的feature map在维度上是一致的。

 

代码验证

选择了pytorch中的torch.nn.Conv2d来做验证。

1.简单介绍网络的输入参数含义

import torch.nn as nn

# 定义一个二维卷积层
conv_layer = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1)

# 假设有一个4维的输入张量 x，形状为 (batch_size, in_channels, height, width)
x = torch.randn(1, 3, 32, 32)

# 在输入张量上应用卷积层
output = conv_layer(x)

# 输出张量的形状为 (batch_size, out_channels, output_height, output_width)

其中，in_channels表示输入张量的通道数，out_channels表示输出张量的通道数（即卷积核的数量），kernel_size表示卷积核的大小，stride表示卷积的步长，padding表示边缘填充的大小。在输入张量上应用卷积层后，输出张量的形状为 (batch_size, out_channels, output_height, output_width)。 

2.为单通道图片设计第一个卷积层，并查看该层的输出

# 设计一个单通道的卷积网络结构
import torch
from torch.autograd import Variable
# 单通道图片模拟输入
input=torch.ones(1,1,64,64)
input=Variable(input)
x=torch.nn.Conv2d(in_channels=1,out_channels=5,kernel_size=3,groups=1)
out=x(input)
print(out.shape)
print(list(x.parameters()))

打印结果

torch.Size([1, 5, 62, 62])
[Parameter containing:
tensor([[[[-0.1166,  0.2381, -0.0446],
          [ 0.0855,  0.1347, -0.2986],
          [-0.3251,  0.2721,  0.2473]]],


        [[[-0.1630,  0.2612,  0.1867],
          [-0.1606, -0.2781, -0.1183],
          [ 0.2221, -0.1114, -0.2046]]],


        [[[-0.2414, -0.2379,  0.0680],
          [ 0.1928, -0.0585,  0.1804],
          [ 0.1891, -0.1915,  0.0281]]],


        [[[-0.3227,  0.0911, -0.0136],
          [-0.2742, -0.2246, -0.1227],
          [ 0.1420,  0.3284, -0.0288]]],


        [[[ 0.2173, -0.1299, -0.2056],
          [-0.2324,  0.2499, -0.1909],
          [ 0.2416, -0.1457, -0.1176]]]], requires_grad=True), 
Parameter containing:
tensor([-0.0273,  0.2994,  0.3226, -0.2969,  0.2965], requires_grad=True)]

这里我们可以看到，第一层的输出结果是有5个feature maps，也就是卷积核的数量。随后我们打印出了第一层的卷积参数，可以看到就是5个卷积核的参数，以及对应的五个bias参数。

3.为RGB三通道图片设计第一个卷积层，并给出参数

# 设计一个3通道的卷积网络结构
import torch
from torch.autograd import Variable
# 模拟RGB三通道图片输入
input=torch.ones(1,3,64,64)
input=Variable(input)
x=torch.nn.Conv2d(in_channels=3,out_channels=5,kernel_size=3,groups=1)
out=x(input)
print(out.shape)
print(list(x.parameters()))

打印输出

torch.Size([1, 5, 62, 62])
[Parameter containing:
tensor([[[[-0.0902, -0.0764,  0.1497],
          [-0.0632, -0.1014, -0.0682],
          [ 0.1309,  0.1173,  0.0268]],

         [[-0.0410, -0.1763,  0.0867],
          [ 0.0771, -0.0969,  0.0700],
          [ 0.1446, -0.0159, -0.1869]],

         [[-0.1278,  0.0244,  0.1861],
          [-0.0180,  0.0529, -0.1475],
          [-0.0562, -0.0487,  0.0659]]],


        [[[ 0.0649, -0.1758, -0.0420],
          [ 0.1287,  0.1500,  0.1027],
          [ 0.0033,  0.1565,  0.1461]],

         [[ 0.0645,  0.0515, -0.0729],
          [ 0.0900,  0.0941,  0.1813],
          [ 0.1846, -0.1075,  0.1861]],

         [[ 0.1489,  0.0536,  0.1510],
          [-0.1070,  0.0748,  0.1619],
          [ 0.1812, -0.0722,  0.1492]]],


        [[[-0.0450, -0.0846,  0.0761],
          [ 0.1049,  0.0492,  0.1556],
          [ 0.1301,  0.0494,  0.0136]],

         [[-0.1303, -0.0979, -0.0331],
          [ 0.0435, -0.0201, -0.1207],
          [ 0.1275, -0.0049, -0.0092]],

         [[ 0.1782,  0.1347,  0.0707],
          [-0.0850,  0.0585,  0.1361],
          [ 0.0917, -0.0156,  0.0407]]],


        [[[ 0.0491,  0.0752,  0.0096],
          [ 0.1599, -0.1281, -0.0937],
          [ 0.1029, -0.1467,  0.1238]],

         [[-0.0651, -0.1169,  0.1772],
          [ 0.0180,  0.1491,  0.0145],
          [ 0.0586,  0.1246,  0.1060]],

         [[-0.1220,  0.0525,  0.1046],
          [ 0.0069,  0.0356,  0.0152],
          [-0.0822, -0.1157, -0.0420]]],


        [[[-0.0679,  0.1752,  0.1020],
          [ 0.0018,  0.0721,  0.1708],
          [-0.0201,  0.1753,  0.0620]],

         [[-0.0023, -0.1203, -0.1113],
          [ 0.1765, -0.1914,  0.0836],
          [-0.0526, -0.1803, -0.0656]],

         [[-0.1735,  0.0795, -0.1867],
          [ 0.1757, -0.0261,  0.0198],
          [-0.1756, -0.0549, -0.0018]]]], requires_grad=True), 
Parameter containing:
tensor([-0.1727,  0.1823,  0.1416, -0.0721, -0.1219], requires_grad=True)]

可以看到，对三通道的图片处理后，输出的也是一样的形状，但是具体再看卷积核，会发现，每个卷积核都有3个通道，而且每个通道的参数是不一样的，但是他们共享一个bias。

深度学习入门基础CNN系列——感受野和多输入通道多输出通道以及批量操作基本概念

本篇文章主要讲解卷积神经网络中的感受野和通道的基本概念，适合于准备入门深度学习的小白，也可以在学完深度学习后将其作为温习。

如果对卷积计算没有概念的可以看本博主的上篇文章深度学习入门基础CNN系列——卷积计算

一、感受野（receptive field）

这里先给出概念，感受野：在卷积神经网络CNN中，决定某一层输出结果中一个元素所对应的输入层的区域大小，被称作感受野（receptive field）。
输出特征图上每个点的数值，是由输入图片上大小为$k_h\times k_w$的区域的元素与卷积核对应每个元素相乘再相加得到的，所以输入图像上$k_h\times k_w$区域内每个元素数值的改变，都会影响输出点的像素值。==我们将这个区域叫做输出特征图上对应点的感受野。==感受野内每个元素数值的变动，都会影响输出点的数值变化。比如$3\times 3$卷积对应的感受野大小就是$3\times 3$，如下图所示：

而通过两层$3\times 3$卷积之后，感受野的大小将会增加到$5\times 5$，如下图所示：

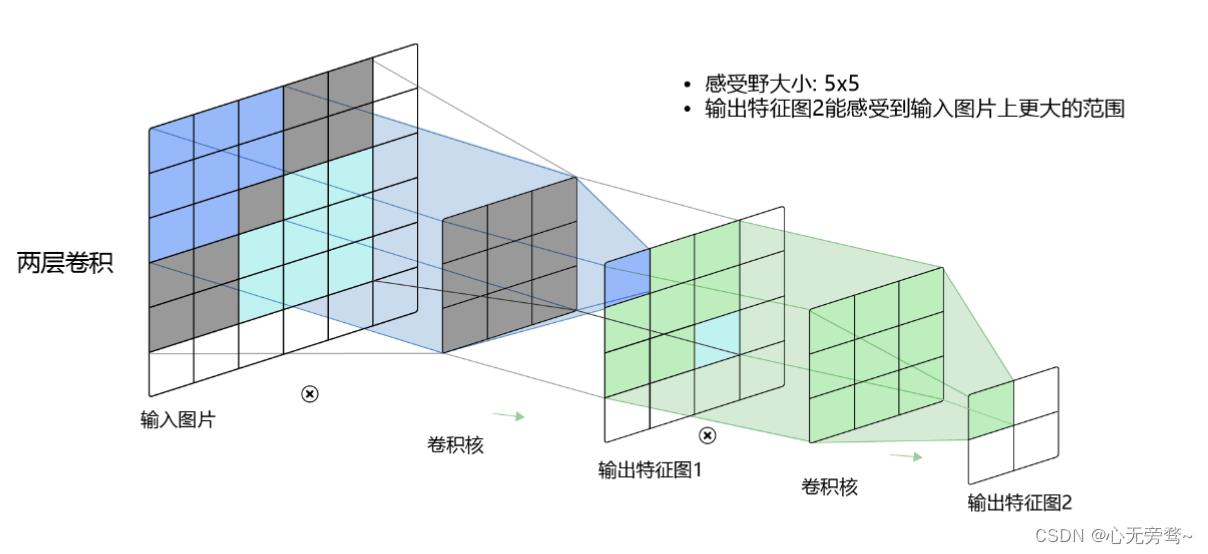
因此，当增加卷积网络深度的同时，感受野将会增大，输出特征图中的一个像素点将会包含更多的图像语义信息。

二、多输入通道、多输出通道和批量操作

前面几篇文章的卷积计算过程比较简单，实际应用时，处理的问题要复杂的多。例如：对于彩色图片有RGB三个通道，需要处理多输入通道的场景。输出特征图往往也会具有多个通道，而且在神经网络的计算中常常是把一个批次的样本放在一起计算，所以卷积算子需要具有批量处理多输入和多输出通道数据的功能，下面将分别介绍这几种场景的操作方式。

2.1 多输入通道场景

在上面的例子中，卷积层的数据是一个2维的数组，但实际上一张图片往往含有RGB三个通道，要计算卷积的输出结果，卷积核的形式也会发生改变，假设输入图片的通道数为$C_{in}$，输入数据的形式是$C_{in}\times H_{in}\times W_{in}$,计算过程如下图所示。

步骤如下：

1. 对每个通道分别设计一个2维数组作为卷积核，卷积核数组的形状为$C_{in}\times K_h\times K_w$。
2. 对任意一个通道$C_{in}\in [0,C_{in})$，分别用大小为$k_h\times k_w$的卷积核在大小为$H_{in}\times W_{in}$的二维数组上做卷积。
3. 将这$C_{in}$个通道的计算结果相加，得到的是一个形状为$H_{out}\times W_{out}$的二维数组。

2.2 多输出通道场景

一般来说，卷积操作的输出特征图也会具有多个通道$C_{out}$，这时候我们需要设计$C_{out}$个维度为$C_{in}\times k_h\times k_w$的卷积核，卷积核数组的维度是$C_{out}\times C_{in}\times k_h\times k_w$，如下图所示：

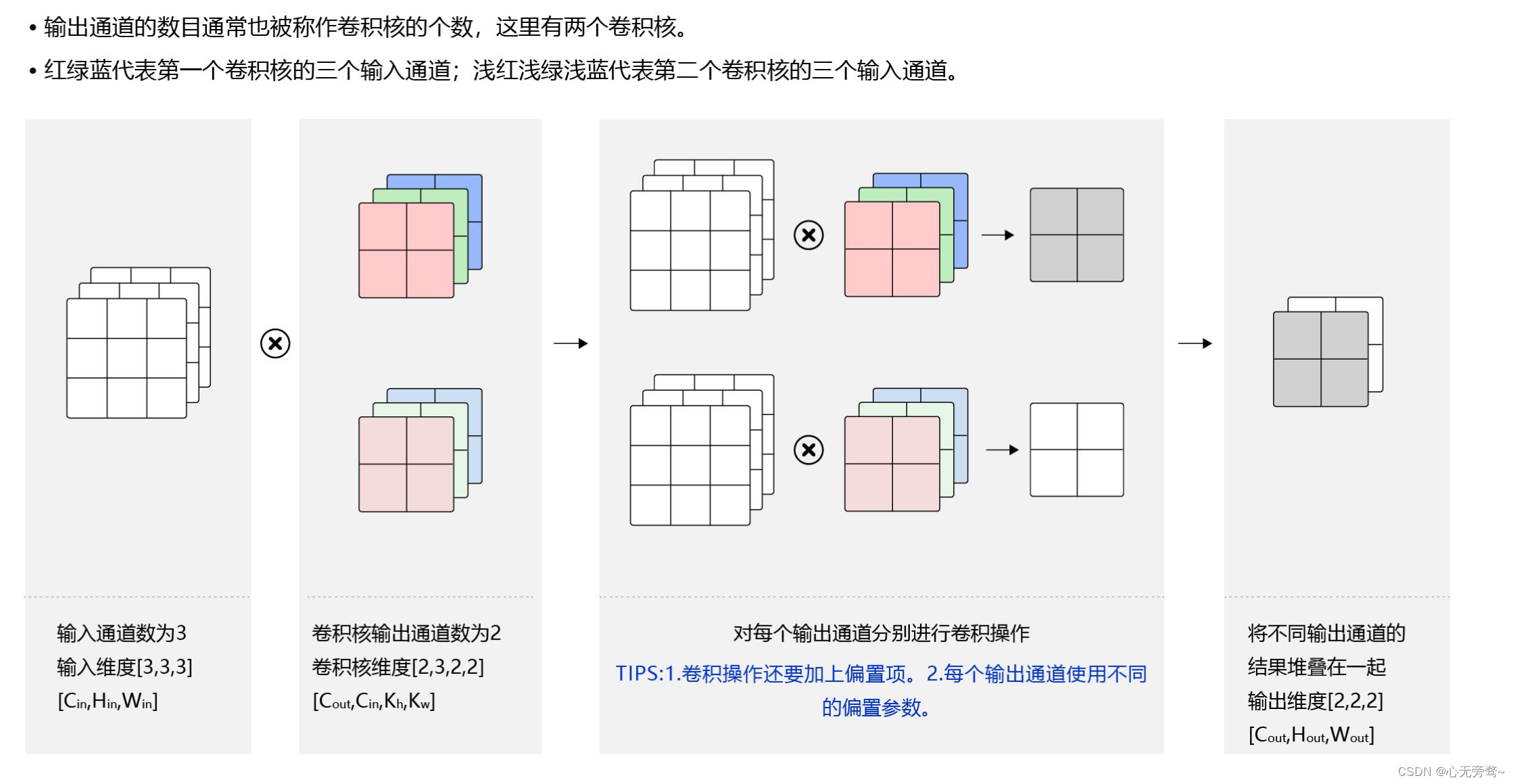
步骤如下：

1. 将任意一输出通道$C_{out}\in [0,C_{out}]$，分别使用上面描述的形状为$C_{in}\times k_h\times k_w$的卷积核对输入图片进行卷积。
2. 对这$C_{out}$个形状为$H_{out}\times W_{out}$的

说明：
通常将卷积核的输出通道数叫做卷积核的个数。

2.3 批量操作

在卷积神经网络的计算中，通常将多个样本放在一起形成一个mini-batch进行批量操作，即输入数据的维度是 $N\times C_{in}\times H_{in}\times W_{in}$。由于会对每张图片使用同样的卷积核进行卷积操作，卷积核的维度与上面多输出通道的情况一样，仍然是$C_{out}\times C_{in}\times k_h\times k_w$，输出特征图的维度是$N\times C_{out}\times H_{out}\times W_{out}$，如下图所示：

附：
深度学习入门基础CNN系列——填充（padding）与步幅（stride）
深度学习入门基础CNN系列——卷积计算