如何用平面几何证明从抛物线的焦点发出的光线经抛物线反射会成为平行线

Posted 2023-03-28

是平面几何!!!!

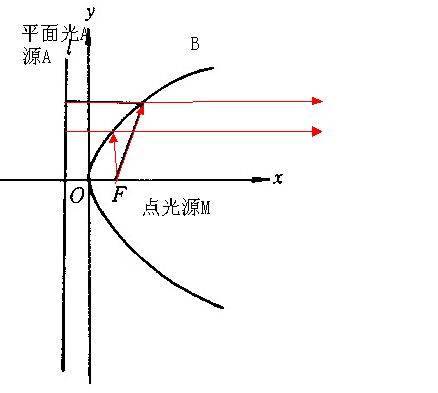
由抛物线定义：抛物线B是到直线A于焦点F距离相等得点的轨迹。

由光的性质知道平面光源A发出的光是平行光，如图所示。根据光程定理如果从焦点F处光源M发出的光经抛物线反射所走的光程等于平面光源A发出光走的光程，则在反射后会变成平行光。

事实上由于抛物线上的点到焦点F和直线A距离相等，光程总是相等的所以结论成立！

参考技术A 抛物线可以用y^2=2px（p>0）而不影响其任意性
焦点P（p/2，0）,任意一点A（y^2/2p,y）
y>0,讨论抛物线上部分，因为对称不影响任意性
这一点对y^2=2px两边对x求导得y'=p/y,则过这一点得切线斜率
就为p/y，与x轴夹角为arctan（p/y）;
而线段PA的斜率为y/(y^2/2p-p/2)与x轴夹角为
arctan（y/(y^2/2p-p/2)）;与过点A的水平线夹角为
pi－arctan（y/(y^2/2p-p/2)），
则与切线的夹角为pi-(pi－arctan（y/(y^2/2p-p/2)))-arctan（p/y）
等于arctan（y/(y^2/2p-p/2))-arctan（p/y）设其为◎
则tan(@)=tan(两角差)
＝y/(y^2/2p-p/2)-p/y/1+(y/(y^2/2p-p/2))*(p/y)化简得
＝y/(y^2/2p-p/2)-p/y/1+p/(y^2/2p-p/2)
＝y-p/y*(y^2/2p-p/2)/y^2/2p-p/2+p
＝y/2+p^2/2y/y^2/2p+p/2
＝p/y
所以可以得到水平线和AP连线与点A的切线夹角恒等
就易得其入射角等于反射角
反射光线全是平行与x轴的 所以都会成平行线