数据结构 - 学习笔记 - 红黑树

Posted 2023-03-03 笑虾

数据结构 - 学习笔记 - 红黑树

• 定义
• 简介
• 知识点
• • 1. 结点属性
  • 2. 前驱、后继
  • 3. 旋转
• 查找
• 插入
• • 父结点为黑色
  • 父结点为红色
  • 1. 有4种情形只需要变色（对应234树4结点）
  • • 1.1. 变色实现平衡
    • 1.2. 递归调整颜色
  • 2. 有4种情形需要旋转 + 变色（对应234树3结点）
• 删除
• • 删除无子结点的黑色结点
  • • 1. 兄弟为红色
    • • 1.1. 找真兄弟（转换的另一种说法）
    • 2. 兄弟为**黑色**
    • • 2.1. 兄弟有红色子节点
      • 2.2. 兄弟无红色子节点
      • • 2.2.1. 父结点为红色
        • 2.2.2. 父结点为**黑色**
  • 时间复杂度
• 辅助脚本
• 参考资料

定义

1. 所有结点非 红 即 黑 。（插入新结点默认红色，然后再按需调整）
2. 根结点 必需是 黑 色。
3. 叶结点 必需是 黑 色。（叶结点是指最末端的空结点。通常在代码中直接用 null 表示，不会创建实际结点。）
4. 红 结点的子结点必需是 黑。有两棵或无子树。（不能有连续的两个红结点）
5. 任意结点到叶节点 经过的 黑 结点数量相同。（别忘记叶结点也是黑色结点 ）

简介

1. 红黑树 是 234树的一种实现，所以学习红黑树前，先看 红黑树前传——234树。
2. 它是一种自平衡的二叉查找树。
   2.1. 二叉查找树的左子树所有结点值都 <= 父，右子树所有结点值都 >= 父。
   2.2. 左右子树也都是二叉查找树。
   2.3. 二叉查找树存在不平衡的情况，极端情况就是个链表。
3. 与AVL（平衡二叉查找树）相比，适当舍弃平衡，换取插入、删除性能提升的同时，兼顾了查找效率。（本质上就是引入了红色结点的概念，它作为填充物，不计入树高，可有可无。因此简少了调平衡的工作量。）
4. 因此红黑树中保障的是 黑 结点的平衡，红 结点作为维持平衡的填充物不影响平衡。
5. 最短路径可以全是 黑 结点。如： 黑→黑→黑
6. 最长路径可以两 黑 夹一 红。如： 黑→红→黑→红→黑
7. 当插入、删除打破平衡时，通过变色和旋转实现再平衡。

知识点

1. 结点属性

颜色、键、左子结点、右子结点、父结点（特殊情况：根结点没有父结点）

2. 前驱、后继

• 前驱结点：从左子树中找最大的结点
• 后继结点：从右子树中找最小的结点

如果我们中序遍历一次，得到从小到大排列的所有元素，就能很直观的看到前驱和后继就是当前结点身边一前一后的两位，删除当前结点，用它们其中一个补位，是最合适的了。

中序遍历结果：[2, 3, 4, 5, 6, 7, 8]
当前结点：5
前驱：4     后继：6

3. 旋转

• 旋转操作不会改变树中序遍历的顺序。
• 旋转操作通过挪东墙补西墙来维护二叉树的平衡。

（对E进行）左旋	（对S进行）右旋

• 总结一下几个结点的规律：

结点	缩写	左旋规律	右旋规律
E	E	E.parent 更新为S E.right更新为S.left	E.right 更新为 S E.parent 更新为 S.parent
S	S	S.left 更新为 E S.parent 更新为 E.parent	S.parent 更新为E S.left更新为E.right
between E and S	BES	BES.parent 更新为 E	BES.parent 更新为 S
less than E	LE	不受任何影响	不受任何影响
greater than S	GS	不受任何影响	不受任何影响
当前子树的父结点	P	如果当前是左子树，更新 P.left	如果当前是右子树，更新 P.right

• 伪代码

// 左旋
S = E.right;
BES = S.left;
E.right = BES;
BES.parent = E;
S.parent = E.parent; // E.parent == S.parent.parent
if(S.parent == null) // S没爹，自己就是根
	S.颜色 = 黑色
else if(E.parent.left == E) // E 是父的左子
	E.parent.left = S;
else					      // E 是父的右子
	E.parent.right = S;

S.left = E;
E.parent = S;

查找

1. 从根结点开始。
2. 对比结点与查找目标，
   2.1. 目标值 = 当前结点：成功找到目标。
   2.2. 目标值 < 当前结点：递归查找左子树。
   2.3. 目标值 > 当前结点：递归查找右子树。

插入

红黑树插入共12种情况：父黑4种，父红8种。

1. 插入的新结点，默认都是红色结点。
2. 插入位置的父结点为黑色。不影响平衡，共 4 种情况。直接插入即可。
   2.1. 父结点无子结点，插入左子结点。
   2.2. 父结点无子结点，插入右子结点。
   2.3. 父结点有红色右子，插入左子。
   2.4. 父结点有红色左子，插入右子。
3. 插入位置的父结点为红色。
   3.1. 对应234树的4结点有4种：祖父黑色，父叔伯都是红色。只需变色实现平衡。
   3.2. 对应234树的3结点有4种： LL、LR、RR、RL。需要旋转 + 变色实现平衡。

父结点为黑色

直接插入即可。

父结点为红色

1. 有4种情形只需要变色（对应234树4结点）

结点情况：父结点为红色且有红色叔伯结点。

1.1. 变色实现平衡

1. 【红黑树】 插入新结点
2. 【红黑树】 父结点、叔伯结点变成黑色，祖父结点变成红色。
   2.1. 父结点与祖父结点调换颜色：满足红结点子必黑的定义。同时对于插入新结点的这一路径来说黑结点数未发生变化。（相当于把祖父的黑色借来用了）
   2.2. 叔伯结点变成黑色：祖父结点原本作为公共的黑结点，挪给另一侧后，当前这条路径就少了一个黑结点。因此 叔伯要站出来变黑维持平衡。
3. 【红黑树】 最后祖父结点更新为当前结点。
   3.1. 如果是根结点，直接染黑。
   3.2. 如果是红色，则需要向上递归调整颜色，一直到根。

1.2. 递归调整颜色

插入新结点 ① 后递归触发变色。
触发递归的原因：曾祖结点是红色，祖父结点染红后出现两个连续红色结点的情况，需要以祖父为当前结点继续进行变色处理。最终到达根结点直接染黑结束。

2. 有4种情形需要旋转 + 变色（对应234树3结点）

结点情况：父结点为红色且无红色叔伯结点。

虽然共有4种 情形，但其中 LR可以转为LL， RL可以转为RR。总之就是有拐弯的，都是转为一条直线，再处理。
1.1. LR 左旋1次，转为 LL。
1.2. LL 右旋1次 + 染色，实现平衡。
2.1. RL 右旋1次，转为 LL。
2.2. RR 左旋1次 + 染色，实现平衡。

删除

删除可能发生在树中的任意位置。结点删除后，可能影响树的平衡，需要重新调整实现平衡。

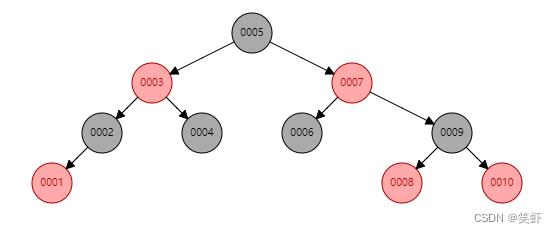
根据将被删除的目标结点的颜色和子结点数量，需要分别处理：

-	当前红色	当前黑色
有两个子结点	同黑色	1. 使用前驱或后继结点内容替换当前结点。（颜色保持不变） 2. 再删除前驱或后继结点。（转变成了对：无子结点的删除）
有一个子结点	直接删除	1. 删除当前结点。 2. 使用子结点填补当前位置，并将颜色设置为黑色。
无子结点	直接删除	1. 当前为根：直接删除。 2. 兄弟为红色：转为黑色再继续处理。 3. 兄弟为黑色：按兄弟有无红色子节点，分别处理。详情如下：

从上面这个表中可以看出只有删除无子结点的黑色结点这一种情况需要我们详细讨论，那么接下来就开始吧：

删除无子结点的黑色结点

1. 兄弟为红色

兄弟为红色：兄弟转为黑色再继续处理。转换方法：

1. 将兄弟结点调整为黑色
2. 将父结点调整为红色。
3. 按当前结点的父结点，进行右旋。

1.1. 找真兄弟（转换的另一种说法）

红色兄弟转黑兄弟。也可以理解为：只有黑色才是真兄弟，红色是塑料兄弟。所以我们要找到真兄弟再干活。

1. 当前是左子结点，就获取父亲的右子结点，判断颜色。如果是黑色，找到兄弟，完成任务。
2. 结果发现是红色，父与兄交换颜色。（不存在连续红，所以父必然是个黑结点）
3. 以父结点为支点，左旋 一次。
4. 现在取父结点的右子结点，就是真兄弟了。（就是原来兄弟的左子结点）

如果当前是右子。同理往左边找就行了。

2. 兄弟为黑色

黑色是真兄弟，可算见到亲人了。可以开始真正的删除操作了。

2.1. 兄弟有红色子节点

借用兄弟子结点修复平衡。

2.2. 兄弟无红色子节点

借助父结点来修复平衡

2.2.1. 父结点为红色

1. 删除当前结点。
2. 兄弟结点调整为红色。
3. 父结点调整为黑色。

2.2.2. 父结点为黑色

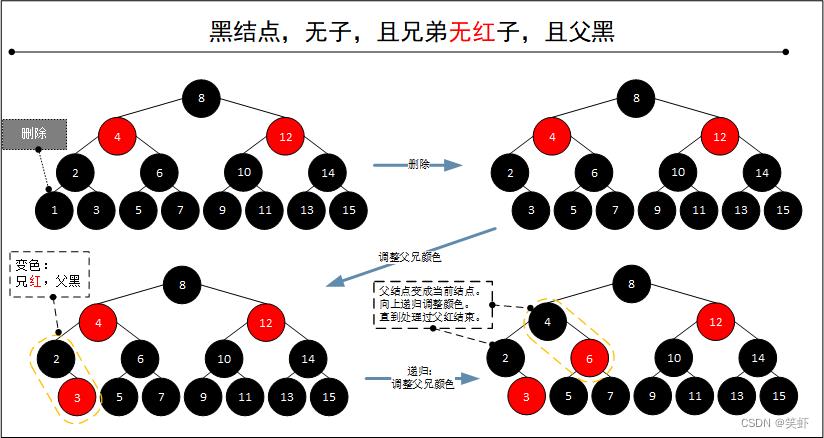
1. 删除当前结点 ①。
2. 兄弟结点 ③ 调整为红色。
3. 将父 结点 ② 作为当前结点，继续处理：
   3.1. 兄弟结点 ⑥ 调整为红色。
   3.2. 判断如果父结点 ④ 为红色把 ④ 染黑。
   3.3. 否则更新 ④ 为 当前结点 递归处理。直到遇到红色父结点并将其染黑实现平衡，或到达根结点为止。

时间复杂度

操作	复杂度
查找	O(lgn)
插入	O(lgn)
删除	O(lgn)

辅助脚本

红黑树可视化演示

var sleep = (delaytime = 1000) => 
  return new Promise(resolve => setTimeout(resolve, delaytime))

async function delayDo(arr, callback = data=>console.log(`数据：$data`), delaytime) 
    var len = arr.length;
    for (let i = 0; i <len  ; i++)         
        await sleep(delaytime);
        callback(arr[i]);
    c
;
// 获取文本框
var [insertTxt, deleteTxt, findTxt] = [...document.querySelectorAll("#AlgorithmSpecificControls [type=Text]")];
// 获取按钮
var [insertBtn, deleteBtn, findBtn] = [...document.querySelectorAll("#AlgorithmSpecificControls [type=Button]")];
var process = 
	insert: function insert(v)	insertTxt.value = v; insertBtn.click();	,
	del: function del(v) deleteTxt.value = v; deleteBtn.click(); ,
	find: function find(v) findTxt.value = v; findBtn.click(); 

// 遍历数组，间隔 n 秒处理一个元素。
function main(arr = [...Array(10).keys()], cb = v=>console.log(v), delaytime=200)
	delaytime = delaytime<200 ? 200 : delaytime
    delayDo(arr, v => cb(v), delaytime);

// 插入元素，间隔 200 毫秒
main([...Array(20).keys()].map(v=>v+1), process.insert, 800);

参考资料

笑虾：数据结构 - 学习笔记 - 红黑树前传——234树

www.cs.usfca.edu：Red/Black Tree 数据结构可视化
Programiz：Red-Black Tree
Algorithmtutor：Red Black Trees (with implementation in C++, Java, and Python)