深度学习方法（二十一）：常用权重初始化方法Xavier，He initialization的推导

Posted 2023-02-24 大饼博士X

文章目录

• 交叉熵目标函数更陡峭
• Xavier initialization [1][4]
• He initialization [2][3]
• • • He init 考虑ReLU函数
    • He init 考虑Leaky ReLU函数
• 结束语
• 参考资料

交叉熵目标函数更陡峭

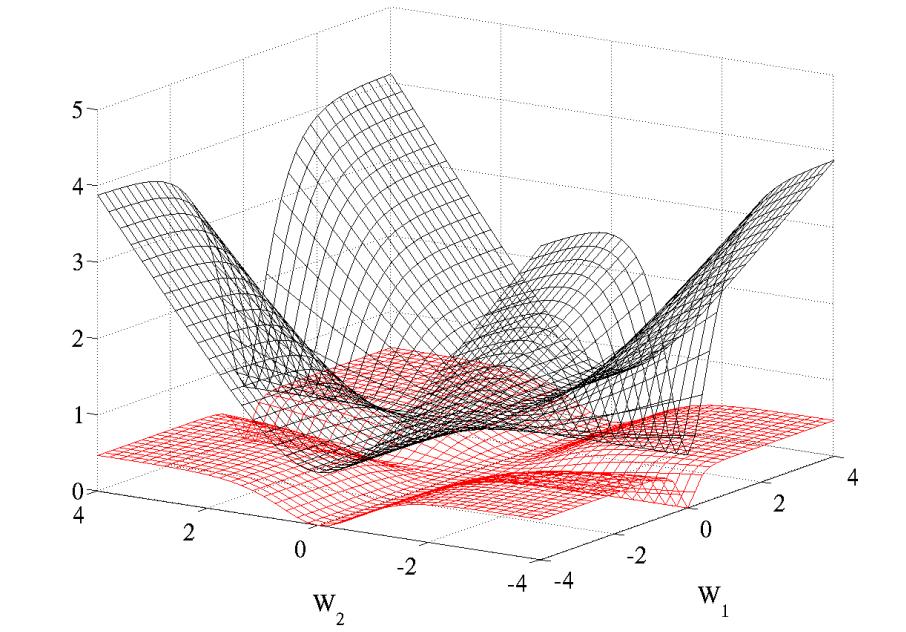
在论文[1]中给了一个图示，一定程度上说明了为什么Cross Entropy用的很多，效果很好。图中上面的曲面表示的是交叉熵代价函数，下面的曲面表示的是二次代价函数，W1和W2分别表示层与层之间的连接权值。

)

在1986年 Rumelhart 已经发现：logistic function 或者叫 conditional log-likelihood function: -log P（y|x) 的效果比 quadratic cost function（平方代价函数）的效果好很多的，原因在于 quadratic cost function（平方代价函数）在训练过程中会出现更多的 plateaus（平坦区域）。文章给出了一个两个参数下的图，图中采用的是具有单隐层的神经网络，激活函数使用的是 tanh 函数，对于输入信号进行随机初始化，可以看到二次代价函数具有更多的 plateaus （平坦区域）。

Xavier initialization [1][4]

早期的参数初始化方法普遍是将数据和参数初始化为标准高斯分布（均值0方差1），但随着神经网络深度的增加，这方法并不能解决梯度消失问题。

那么我们应该怎么通过初始化来缓解这个问题呢？
论文中首先给出了一个启发式的方法，想法是初始化值和神经元的输入个数有关：

We initialized the biases to be 0 and the weights Wij at each layer with the following commonly used heuristic, where U[−a, a] is the uniform distribution in the interval (−a, a) and n is the size of the previous layer (the number of columns of W)

$$\begin{gathered} W\sim U[-\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}}] \\ Var(W)=\frac{1}{3n} \end{gathered}$$

上面式子中，$W\sim$表示其中的每一个元素$W_{ij}$都是符合一个均匀分布的。其中n表示本层的输入size，也就是上一层的输出size。我们知道随机变量在[a,b] 间的均匀分布的方差为
$$Var=\frac{(b-a{)}^2}{12}$$
所以得到权重参数的方差是1/3n。先记一下，后面分析会讲到。

为了便于研究，作者假设使用线性激活函数$f(x)$，且在零点导数$f^{\prime }(0)=1$。实际上，作者研究的是参数的线性区域，可以认为是对任务的一个简化。

对于一层网络：
$$f(\text{x})=\sum _i^n{w}_i{x}_i+b$$
输出的方差：
$$Var(f(\text{x}))=\sum _i^{n}Var(w_i{x}_i)$$
其中每一项：
$$Var(w_i{x}_i)=E[w_i{]}^{2}Var(x_i)+E[x_i{]}^{2}Var(w_i)+Var(w_i)Var(x_i)$$

当我们假设输入和权重都是0均值时（目前有了BN之后，每一层的输入也较容易满足），即$E[x_i]=E[w_i]=0$，上式可以简化为：

$$Var(w_i{x}_i)=Var(w_i)Var(x_i)$$

由于w和x独立同分布，那么输出的方差就是

$$Var(f(\text{x}))=nVar(w_i)Var(x_i)$$

我们发现，输出的方差是和输入的方差是一个线性倍数关系。假设$z^i$是第$i$层的输入向量，$s^i$是第$i$层激活函数的输入，$f$表示激活函数

$$\begin{gathered} {\text{s}}^i={\text{z}}^i{W}^i+{\text{b}}^i \\ {\text{z}}^{i+1}=f({\text{s}}^i) \\ {\text{s}}^{i+1}={\text{z}}^{i+1}{W}^{i+1}+{\text{b}}^{i+1} \end{gathered}$$

可以得到：
对于一个多层的网络，某一层的方差可以用累积的形式表达：
$$Var[z^i]=Var[x]\prod _{i^{\prime }=0}^{i-1}{n}_{i^{\prime }}Var[W^{i^{\prime }}]$$

求反向我们可以得到（假设 f ′ ( s k i ) ≈