Java 浮点数精度丢失
问题引入
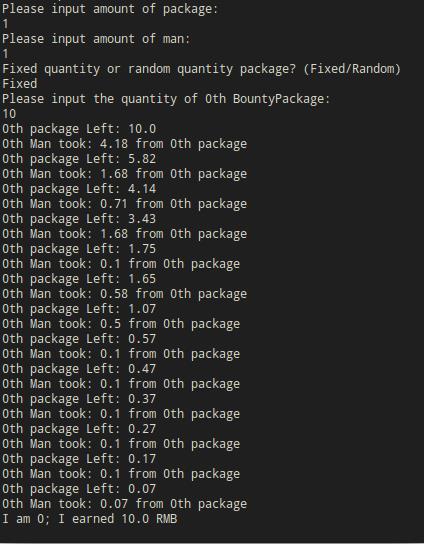
昨天帮室友写一个模拟发红包抢红包的程序时,对金额统一使用的 double 来建模,结果发现在实际运行时程序的结果在数值上总是有细微的误差,程序运行的截图:
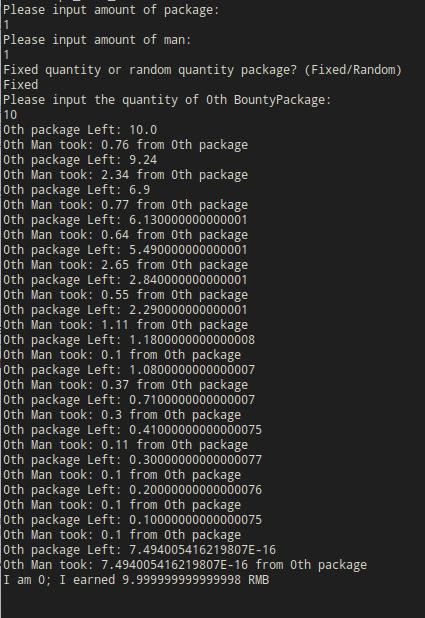
输入依次为:红包个数,抢红包的人数,选择固定金额红包还是随机金额红包,每个红包的金额(此例只有一个红包)。
注意到程序最后的结果是有问题的,我们只有一个金额为 10 的红包,一个人去抢,所以正确结果应该为这个人抢到了 10 RMB。
为了使问题更加明显,我们测试一个更加简单的例子:
public class SimpleTest {
public static void main(String[] args) {
System.out.println(1.2 - 1);
}
}
////
output:
0.19999999999999996 (不是 0.2)
为什么发生了我们预期之外的问题?
为什么?
从 \\(\\frac{1}{3}\\) 到 \\(0.333...\\)
我们先抛开 Java 不管,来看一下这个问题,如何用十进制小数表示 \\(\\frac{1}{3}\\) 。
首先我们讨论如何借用数轴表示 十进位小数 。如果我们将一个数轴分为 10 等份,100 等份(相当于 10 等份的每个单位区间再分 10 份),1000 等份,等等个相等的线段,则其中每个点对应着 一个十进制小数。
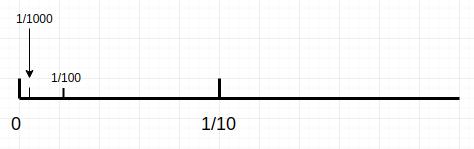
因此一个十进制小数可以表示为不同精度单位的加权(即乘以系数)和。
比如 \\(0.12 = \\frac{1}{10} + \\frac{2}{100}\\) ,它对应的点位于区间长为 \\(10^{-1}\\) 的第二个区间内(\\(\\frac{1}{10}\\) 后),是长为 \\(10^{-2}\\) 的第二个子子区间的右端点。
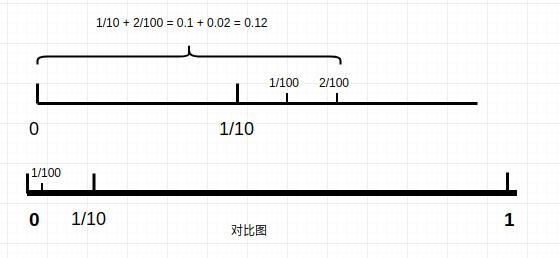
一个十进制小数,其后有 n 个数码,它的加权式可以写成$$f = z + a_1{10^{-1}} + a_2{10^{-2}} + a_3{10^{-3}} + ... + a_n{10^{-n}};$$ 这里 z 是一整数,而 a 是十分之一,百分之一 等等的数码,其中 \\(a\\in [0,1,2,...,9]\\) 。另外,因为 \\(10^{-n} = \\frac{1}{10^n}\\) ,所以十进位小数都可以写成一个分数的形式。比如 $$f = 1.134 = 1 + \\frac{1}{10} + \\frac{3}{100} + \\frac{4}{1000} = \\frac{1134}{1000}$$ 。如果分子和分母有公因子,那么分数还可以进行约分。另一方面,如果分母不是 10 的某次幂的因子(即无法通过将分母乘以一个数得到 10 的某次幂(10,100,1000)来通分),那么这个分数不能表示为十进制小数。
十进制小数举例:$$\\frac{1}{5} = \\frac{2}{10} = 0.2; \\frac{1}{250} = \\frac{4}{1000} = 0.004$$ 而非十进制小数如:$ \\frac{1}{3}$,它不能写成 n 位十进制小数的形式,因为 $$ \\frac{1}{3} = \\frac{b}{10^n}$$ 意味着 $$3b = 10^n$$ ,而这个结果是不成立的。我们根据之前得到的十进制小数的表达形式可以得知,非十进制小数将不会坐落在十进制数轴的任何端点上(如果在端点上那么我们就可以通过加权式来表达它,他也就是十进制小数了)。但是,虽然无法精确的在十进制数轴上表达他,我们却可以采用无穷逼近的思想,去无限的接近它。
首先将 \\(\\frac{1}{3}\\) 通分,$$ \\frac{1}{3} = \\frac{10}{30}$$ ;然后我们在数轴上寻找,最接近它的左端点为 $$\\frac{9}{30} = \\frac{3}{10}$$ ,右端点为 $$\\frac{12}{30} = \\frac{4}{10}$$ ,\\(\\frac{1}{3}\\) 位于这个区间中的某一点,再进一步,做差 \\(\\frac{10}{30} - \\frac{9}{30} = \\frac{1}{30}\\) ,这时我们取左端点为 \\(\\frac{3}{10}\\) 后距离 \\(\\frac{1}{3}\\) 在数轴上剩余的距离,再次进行通分,\\(\\frac{1}{30} = \\frac{10}{300}\\),现在最接近他的左端点为 \\(\\frac{9}{300} = \\frac{3}{100}\\) ,以此类推,我们取到的左端点将是 \\(\\frac{3}{10},\\frac{3}{100},\\frac{3}{1000},...\\) ,而最后,\\(\\frac{1}{3}\\) 就等于这些小的间距的加和(从原点到 \\(\\frac{1}{3}\\) 所在点的距离):$$ \\frac{1}{3} = \\frac{3}{10} + \\frac{3}{100} + \\frac{3}{1000} + ...$$ 用十进制小数表示也即:$$\\frac{1}{3} = 0.3 + 0.03 + 0.003 + ... = 0.333...$$ 无限接近但是永远不等于 \\(\\frac{1}{3}\\) 。在某种精度下,我们可以得到这样的一个近似值 \\(0.333333333334\\) 。
二进制小数
之前我们讨论的是在十进制的情况下,但计算机比较擅长使用二进制来表示数,所以我们接下来考虑如果二进制情况下,是否会出现之前在十进制中出现的无法精确表示的情况。(答案是肯定的,这也是我们的主题所在)
和十进制下相同,对于二进制,式:$$f = z + a_1{2^{-1}} + a_2{2^{-2}} + a_3{2^{-3}} + ... + a_n{2^{-n}};$$ 仍成立,不过基数变为了 2。(\\(z\\) 此时是二进制整数)
十进制下,我们对数轴每次进行 10 等划分,现在我们对数轴的单位长度每次进行 2 等划分。即:
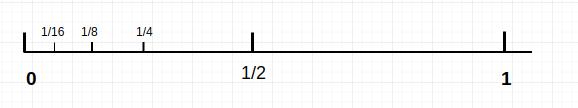
在这种情况下,我们举一个简单的存在精度丢失的例子:十进制 0.1 的二进制表达
由于 $$0.1 = \\frac{1}{10^1};$$ 在这里我们要求分母必须为 2 的某次幂(\\(2,4,8,16,...)\\)的因子,而 0.1 的 分母为 10 ,显然不符合要求。所以无法用二进制小数精确表示,只能近似。近似的过程如下:
与 0.1 最为接近的左端点是 $$\\frac{1}{16} = 0.0625$$ ,右端点为 \\(\\frac{1}{8} = 0.125\\) ,0.1 在这个区间中的某一点上。做差:$$0.1 - 0.0625 = 0.0375$$ ;最接近的左端点为:$$\\frac{1}{32} = 0.03125$$ ,如此往复,最终我们得到这样一个式子:$$0.1 = \\frac{1}{16} + \\frac{1}{32} + \\frac{1}{256} + ...$$ 。该式子只会无限接近 0.1 但是不会等于他。
我们当然不会忘记计算机组成原理课上学的计算十进制小数转换二进制的方法,这个方法可以让我们快速的求出二进制小数部分:
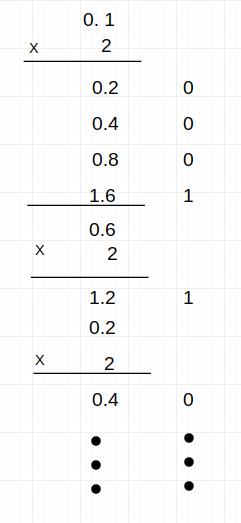
最后的结果是:$$0.1_{10} = 0.000110011001100_2 ...$$ 这里的小数位的每一位就是 式:$$f = z + a_1{2^{-1}} + a_2{2^{-2}} + a_3{2^{-3}} + ... + a_n{2^{-n}};$$ 中的权值 \\(a\\) 。
当我们精确位数为小数点后四位时,在计算机中的 0.1 的表示理论上就是 \\(1 * \\frac{1}{16} = 0.625\\) ,当精确位数为十位时,即表示为:\\(0.0001100110\\) ,此时 \\(0.1\\) 的近似值为:\\(0.09999847412109375\\) 。如果精确位数为 27 此时值为:\\(0.0999999940395355224609375\\) 精确位数越高,值越接近实际值。
所以对于我们在开始时举的例子 \\(0.2\\) ,情况是相似的,我们可以轻松的理解它。
在 Java 中怎么解决这个问题?
前文主要从数学的角度讨论了不同进制间数的表示存在的精度问题,现在回归到最初的问题,Java 中浮点数的精度丢失。我们知道,编程语言对数学中的数集建模是采用二进制数方式,而 计算机内存是有限 的,所以计算必然是在有限精度内进行,这种情况下精度丢失不可避免。对于 Java 中的原始类型 float、double 一般性的建议是使用他们进行科学数值计算,而对于像金额这一类生活中常见的数值类别,推荐使用 java.math.BigDecimal 类来建模(当然有精力也可自己造一个轮子)。该类可以避免之前讨论的精度问题。
需要注意的是,在使用 BigDecimal 时,一定要将需要计算的数值作为 字符串 传递给构造函数,不然仍会发生精度丢失问题。
在使用了 BigDecimal 修改我的程序后,它工作的正常多了:)。
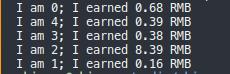
设置多个人并发抢红包:
抢红包过程(截取部分):
结果:
最后
写这篇文章主要是因为最近在看科普书 《什么是数学》,恰好看到 十进制小数和无穷小数 部分,又遇到了 Java 精度丢失问题,然后惊喜的发现二者之间紧密的联系,于是写了这篇文章。
数学真奇妙。
作者:Skipper
出处:http://www.cnblogs.com/backwords/p/9826773.html
本博客中未标明转载的文章归作者 Skipper 和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。