统计学 ROC曲线

Posted 2023-04-26

参考技术A 来自wiki的图：
这个由actual和predicted构成的m乘n列联表叫做confusion matrix(混淆矩阵)。在下面的例子里，actual就是用结肠镜金标准鉴别的肠癌患者，predicted用粪便隐血预测的肠癌患者。

2*2表里，
左上角叫True positive(tp) 真阳
左下角叫false negative(fn) 假阴
右上角叫false positive(fp) 假阳
右下角叫true negative(tn) 真阴

正确率(Precision)等于tp/tp+fp
真阳性率(TPR)、敏感度(sensitivity)、召回率(recall)等于tp/tp+fn
真阴性率(TNR)、特异性(specificity)等于tn/fp+tn
假阴性率(FNR)、漏诊率等于fn/tp+fn
假阳性率(FPR)、误诊率等于fp/fp+tn
sensitivity：coorectly identify patients with bowel cancer.
specificity：coorectly identify patients without bowel cancer.

真实的希望是左上和右下的值特别大，
因此在ROC曲线里就是希望纵坐标(TPR)大，而横坐标(FPR)小。

Sklearn机器学习——ROC曲线ROC曲线的绘制和AUC面积运用ROC曲线找到最佳阈值

目录

1 ROC曲线

2 ROC曲线的绘制

2.1 Sklearn中的ROC曲线和AUC面积

2.2 利用ROC曲线找到最佳阈值

1 ROC曲线

上篇博客介绍了ROC曲线的概率和阈值还有SVM实现概率预测：重要参数probility ,接口predict_function以及decision_function

Sklearn机器学习——样本不平衡问题解决、精确率、召回率、ROC曲线_chelsea_tongtong的博客-CSDN博客

2 ROC曲线的绘制

ROC是一条以不同阈值下的假正率FPR为横坐 标，不同阈值下的召回率Recall为纵坐标的曲线。简单地来说，只要我们有数据和模型，我们就可以在python中绘 制出我们的ROC曲线。思考一下，我们要绘制ROC曲线，就必须在我们的数据中去不断调节阈值，不断求解混淆矩 阵，然后不断获得我们的横坐标和纵坐标，最后才能够将曲线绘制出来。接下来，我们就来执行这个过程：

• 假正率：1-特异度
• 特异度：00/真实值为0（00+01）
• 假正率：01/（00+01）

00/all true 0 1-特异度
#FPR #被我们预测错误的0占所有真正为0的样本的比例
cm[1,0]/cm[1,:].sum()

#概率 clf_proba.predict_proba(X)[:,1] #我的类别1下面的概率
#阈值，每一个阈值都对应着一次循环，每一次循环，都要有一个混淆矩阵，要有一组假正率vsRecall
#np.lispance(概率最小值，概率最大值，55，endpoint=False) #不要取到最大值
#if i > 概率最大值, 返回1

• 概率 clf_proba.predict_proba(X)[:,1] 表示我的类别1下面的概率
• 阈值，每一个阈值都对应着一次循环，每一次循环，都要有一个混淆矩阵，要有一组假正率和Recall
• np.lispance(概率最小值，概率最大值，55，endpoint=False)不要取到最大值，if i > 概率最大值, 返回1 

#开始绘图
probrange = np.linspace(clf_proba.predict_proba(X)[:,1].min(),clf_proba.predict_proba(X)[:,1].max(),num=50,endpoint=False)

from sklearn.metrics import confusion_matrix as CM, recall_score as R
import matplotlib.pyplot as plot

recall = []
FPR = []#假正率

for i in probrange:
    y_predict = []
    for j in range(X.shape[0]):
        if clf_proba.predict_proba(X)[j,1] > i:
            y_predict.append(1)
        else:
            y_predict.append(0)
    cm = CM(y,y_predict,labels=[1,0])
    recall.append(cm[0,0]/cm[0,:].sum())
    FPR.append(cm[1,0]/cm[1,:].sum())

recall.sort()
FPR.sort()

plt.plot(FPR,recall,c="red")
plt.plot(probrange+0.05,probrange+0.05,c="black",linestyle="--")
plt.show()

复习append:向列表末尾追加元素

a = ["apple", "banana", "cherry"]

b = ["Ford", "BMW", "Volvo"]

a.append(b)

print(a)

['apple', 'banana', 'cherry', ['Ford', 'BMW', 'Volvo']]

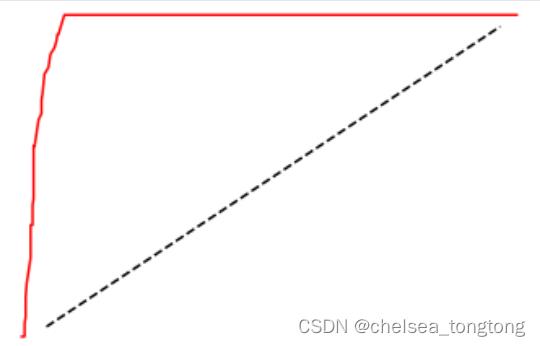
 现在我们就画出了ROC曲线了，那我们如何理解这条曲线呢？先来回忆一下，我们建立ROC曲线的根本目的是找寻 Recall和FPR之间的平衡，让我们能够衡量模型在尽量捕捉少数类的时候，误伤多数类的情况会如何变化。横坐标 是FPR，代表着模型将多数类判断错误的能力，纵坐标Recall，代表着模型捕捉少数类的能力，所以ROC曲线代表 着，随着Recall的不断增加，FPR如何增加。我们希望随着Recall的不断提升，FPR增加得越慢越好，这说明我们可 以尽量高效地捕捉出少数类，而不会将很多地多数类判断错误。所以，我们希望看到的图像是，纵坐标急速上升， 横坐标缓慢增长，也就是在整个图像左上方的一条弧线。这代表模型的效果很不错，拥有较好的捕获少数类的能 力。

总结：对于一条凸型ROC曲线来说，曲线越靠近左上角越好，越往下越糟糕，曲线 如果在虚线的下方，则证明模型完全无法使用。但是它也有可能是一条凹形的ROC曲线。对于一条凹型ROC曲线来 说，应该越靠近右下角越好，凹形曲线代表模型的预测结果与真实情况完全相反。

好了，现在我们有了这条曲线，我们的确知道模型的效果还算是不错了。但依然非常摸棱两可，有没有具体的数字 来帮助我们理解ROC曲线和模型的效果呢？的确存在，这个数字就叫做AUC面积，它代表了ROC曲线下方的面积， 这个面积越大，代表ROC曲线越接近左上角，模型就越好。AUC面积的计算比较繁琐，因此，我们使用sklearn来 帮助我们。接下来我们来看看，在sklearn当中，如何绘制我们的ROC曲线，找出我们的的AUC面积。

2.1 Sklearn中的ROC曲线和AUC面积

  在sklearn中，我们有帮助我们计算ROC曲线的横坐标假正率FPR，纵坐标Recall和对应的阈值的类 sklearn.metrics.roc_curve。同时，我们还有帮助我们计算AUC面积的类。sklearn.metrics.roc_auc_score。在一些 比较老旧的sklearn版本中，我们使用sklearn.metrics.auc这个类来计算AUC面积，但这个类即将在0.22版本中被 放弃，因此建议大家都使roc_auc_score。来看看我们的这两个类：

sklearn.metrics.roc_curve((y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True)

y_true	数组，形状 = [n_samples]，真实标签
y_score	数组，形状 = [n_samples]，置信度分数，可以是正类样本的概率值，或置信度分数，或者 decision_function返回的距离
pos_label	整数或者字符串, 默认None，表示被认为是正类样本的类别
sample_weight	形如 [n_samples]的类数组结构，可不填，表示样本的权重
drop_intermediate	布尔值，默认True，如果设置为True，表示会舍弃一些ROC曲线上不显示的阈值点，这对 于计算一个比较轻量的ROC曲线来说非常有用
这个类以此返回	FPR，Recall以及阈值。

•  此时的threshold就不是一个概率值，而是距离值中的阈值了，所以它可以大于1，也可以为负。因为距离就是可大可小，可正可负。
• decision_function只会生成一列距离，样本的类别由距离的符号来判断。所以decision_function是有正有负的一维数组。

 from sklearn.metrics import roc_curve
FPR, recall, thresholds = roc_curve(y,clf_proba.decision_function(X), pos_label=1)
FPR
recall
thresholds 

array([  3.18236076,   2.18236076,   1.48676267,   1.35964325,
         1.33920817,   1.14038015,   1.13383091,   1.00003406,
         0.85085628,   0.84476439,   0.78571364,   0.60568093,
         0.5389064 ,   0.46718521,   0.44396046,   0.03907036,
        -0.07011269,  -0.10668727,  -0.1258212 ,  -0.13845693,
        -0.14034183,  -0.16790648,  -0.2040958 ,  -0.22137683,
        -0.24381463,  -0.26762451,  -0.34446784,  -0.3467975 ,
        -0.39182241,  -0.40676459,  -0.4589064 ,  -0.46310299,
        -0.49195707,  -0.5088941 ,  -0.53560561,  -0.55152081,
        -0.62628865,  -0.67580418,  -0.78127198,  -0.79874442,
        -0.88438995,  -0.91257798,  -1.01417607,  -1.08601917,
       -10.31959605])

AUC面积的分数使用以上类来进行计算，输入的参数也比较简单，就是真实标签，和与roc_curve中一致的置信度 分数或者概率值。

sklearn.metrics.roc_auc_score ((y_true, y_score, average=’macro’, sample_weight=None, max_fpr=None))

min = 0
max = 1
area = AUC(y,clf_proba.decision_function(X))
plt.figure()
plt.plot(FPR, recall, color='red',
         label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black',linestyle='--')
plt.xlim([-0.05, 1.05])#不是在0，1是因为怕挤着不太好看
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()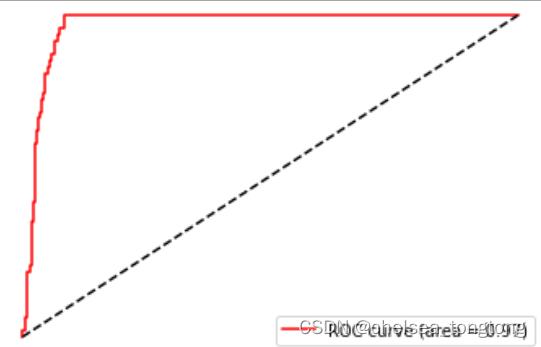

如此就得到了我们的ROC曲线和AUC面积，可以看到，SVM在这个简单数据集上的效果还是非常好的。并且大家可 以通过观察我们使用decision_function画出的ROC曲线，对比一下我们之前强行使用概率画出来的曲线，两者非常 相似，所以在无法获取模型概率的情况下，其实不必强行使用概率，如果有置信度，那也使可以完成我们的ROC曲 线的。感兴趣的小伙伴可以画一下如果带上class_weight这个参数，模型的效果会变得如何。

2.2 利用ROC曲线找到最佳阈值

现在，有了ROC曲线，了解了模型的分类效力，以及面对样本不均衡问题时的效力，那我们如何求解我们最佳的阈 值呢？我们想要了解，什么样的状况下我们的模型的效果才是最好的。回到我们对ROC曲线的理解来：ROC曲线反 应的是recall增加的时候FPR如何变化，也就是当模型捕获少数类的能力变强的时候，会误伤多数类的情况是否严 重。我们的希望是，模型在捕获少数类的能力变强的时候，尽量不误伤多数类，也就是说，随着recall的变大，FPR 的大小越小越好。所以我们希望找到的最有点，其实是Recall和FPR差距最大的点。这个点，又叫做约登指数。

• tolist函数用来将数组转化为列表
• list.index(最大值)用来返回列表最大值的索引

max((recall - FPR).tolist())
#lits.index(最大值) #返回这个最大值在list中的索引

maxindex = (recall - FPR).tolist().index(max(recall - FPR))
maxindex #recall, FPR
thresholds[maxindex] #decision_function生成的置信度来说
#我们可以在图像上来看看这个点在哪里
plt.scatter(FPR[maxindex],recall[maxindex],c="black",s=30)

#把上述代码放入这段代码中：
plt.figure()
plt.plot(FPR, recall, color='red',
         label='ROC curve (area = %0.2f)' % area)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.scatter(FPR[maxindex],recall[maxindex],c="black",s=30)
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('Recall')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()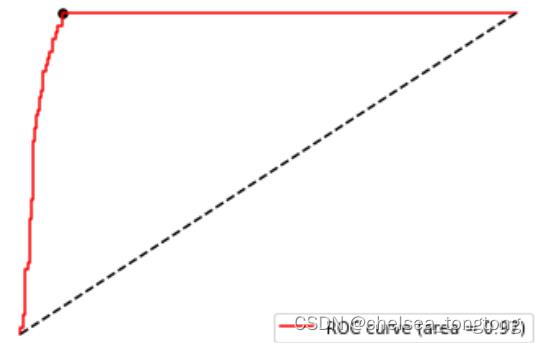

 最佳阈值就这样选取出来了，由于现在我们是使用decision_function来画ROC曲线，所以我们选择出来的最佳阈值 其实是最佳距离。如果我们使用的是概率，我们选取的最佳阈值就会使一个概率值了。只要我们让这个距离/概率 以上的点，都为正类，让这个距离/概率以下的点都为负类，模型就是最好的：即能够捕捉出少数类，又能够尽量 不误伤多数类，整体的精确性和对少数类的捕捉都得到了保证。 而从找出的最优阈值点来看，这个点，其实是图像上离左上角最近的点，离中间的虚线最远的点，也是ROC曲线的 转折点。如果没有时间进行计算，或者横坐标比较清晰的时候，我们就可以观察转折点来找到我们的最佳阈值。