实例详解贝叶斯推理的原理

Posted 2023-04-26

参考技术A                                                实例详解贝叶斯推理的原理

姓名：余玥     学号：16010188033

【嵌牛导读】：贝叶斯推理是由英国牧师贝叶斯发现的一种归纳推理方法，后来的许多研究者对贝叶斯方法在观点、方法和理论上不断的进行完善，最终形成了一种有影响的统计学派，打破了经典统计学一统天下的局面。贝叶斯推理是在经典的统计归纳推理——估计和假设检验的基础上发展起来的一种新的推理方法。与经典的统计归纳推理方法相比，贝叶斯推理在得出结论时不仅要根据当前所观察到的样本信息，而且还要根据推理者过去有关的经验和知识。

【嵌牛鼻子】：贝叶斯推理/统计

【嵌牛提问】：贝叶斯推理的原理是什么？如何通过实例理解贝叶斯原理？

【嵌牛正文】：

贝叶斯推理是一种精确的数据预测方式。在数据没有期望的那么多，但却想毫无遗漏地，全面地获取预测信息时非常有用。

提及贝叶斯推理时，人们时常会带着一种敬仰的心情。其实并非想象中那么富有魔力，或是神秘。尽管贝叶斯推理背后的数学越来越缜密和复杂，但其背后概念还是非常容易理解。简言之，贝叶斯推理有助于大家得到更有力的结论，将其置于已知的答案中。

贝叶斯推理理念源自托马斯贝叶斯。三百年前，他是一位从不循规蹈矩的教会长老院牧师。贝叶斯写过两本书，一本关于神学，一本关于概率。他的工作就包括今天著名的贝叶斯定理雏形，自此以后应用于推理问题，以及有根据猜测（educated guessing）术语中。贝叶斯理念如此流行，得益于一位名叫理查·布莱斯牧师的大力推崇。此人意识到这份定理的重要性后，将其优化完善并发表。因此，此定理变得更加准确。也因此，历史上将贝叶斯定理称之为 Bayes-Price法则。

译者注：educated guessing 基于(或根据)经验(或专业知识、手头资料、事实等)所作的估计(或预测、猜测、意见等)

影院中的贝叶斯推理

试想一下，你前往影院观影，前面观影的小伙伴门票掉了，此时你想引起他们的注意。此图是他们的背影图。你无法分辨他们的性别，仅仅知道他们留了长头发。那你是说，女士打扰一下，还是说，先生打扰一下。考虑到你对男人和女人发型的认知，或许你会认为这位是位女士。（本例很简单，只存在两种发长和性别）

现在将上面的情形稍加变化，此人正在排队准备进入男士休息室。依靠这个额外的信息，或许你会认为这位是位男士。此例采用常识和背景知识即可完成判断，无需思考。而贝叶斯推理是此方式的数学实现形式，得益于此，我们可以做出更加精确的预测。

我们为电影院遇到的困境加上数字。首先假定影院中男女各占一半，100个人中，50个男人，50个女人。女人中，一半为长发，余下的25人为短发。而男人中，48位为短发，两位为长发。存在25个长发女人和2位长发男人，由此推断，门票持有者为女士的可能性很大。

100个在男士休息室外排队，其中98名男士，2位女士为陪同。长发女人和短发女人依旧对半分，但此处仅仅各占一种。而男士长发和短发的比例依旧保持不变，按照98位男士算，此刻短发男士有94人，长发为4人。考虑到有一位长发女士和四位长发男士，此刻最有可能的是持票者为男士。这是贝叶斯推理原理的具体案例。事先知晓一个重要的信息线索，门票持有者在男士休息室外排队，可以帮助我们做出更好的预测。

为了清晰地阐述贝叶斯推理，需要花些时间清晰地定义我们的理念。不幸的是，这需要用到数学知识。除非不得已，我尽量避免此过程太过深奥，紧随我查看更多的小节，必定会从中受益。为了大家能够建立一个基础，我们需要快速地提及四个概念：概率、条件概率、联合概率以及边际概率。

概率

一件事发生的概率，等于该事件发生的数目除以所有事件发生的数目。观影者为一个女士的概率为50位女士除以100位观影者，即0.5 或50%。换作男士亦如此。

而在男士休息室排列此种情形下，女士概率降至0.02，男士的概率为0.98。

条件概率

条件概率回答了这样的问题，倘若我知道此人是位女士，其为长发的概率是多少？条件概率的计算方式和直接得到的概率一样，但它们更像所有例子中满足某个特定条件的子集。本例中，此人为女士，拥有长发的人士的条件概率，P(long hair | woman)为拥有长发的女士数目，除以女士的总数，其结果为0.5。无论我们是否考虑男士休息室外排队，或整个影院。

同样的道理，此人为男士，拥有长发的条件概率，P(long hair | man)为0.4，不管其是否在队列中。

很重要的一点，条件概率P(A | B)并不等同于P(B | A)。比如P(cute | puppy)不同于P(puppy | cute)。倘若我抱着的是小狗，可爱的概率是很高的。倘若我抱着一个可爱的东西，成为小狗的概率中等偏下。它有可能是小猫、小兔子、刺猬，甚至一个小人。

联合概率

联合概率适合回答这样的问题，此人为一个短发女人的概率为多少？找出答案需要两步。首先，我们先看概率是女人的概率，P(woman)。接着，我们给出头发短人士的概率，考虑到此人为女士，P(short hair | woman)。通过乘法，进行联合，给出联合概率，P(woman with short hair) = P(woman) * P(short hair | woman)。利用此方法，我们便可计算出我们已知的概率，所有观影中P(woman with long hair)为0.25，而在男士休息室队列中的P(woman with long hair)为0.1。不同是因为两个案例中的P(woman)不同。

相似的，观影者中P(man with long hair) 为0.02，而在男士休息室队列中概率为0.04。

和条件概率不同，联合概率和顺序无关，P(A and B)等同于P(B and A)。比如，同时拥有牛奶和油炸圈饼的概率，等同于拥有油炸圈饼和牛奶的概率。

边际概率

我们最后一个基础之旅为边际概率。特别适合回答这样的问题，拥有长发人士的概率？为计算出结果，我们须累加此事发生的所有概率——即男士留长发的概率加女士留长发的概率。加上这两个概率，即给出所有观影者P(long hair)的值0.27，而男休息室队列中的P(long hair)为0.05。

贝叶斯定理

现在到了我们真正关心的部分。我们想回答这样的问题，倘若我们知道拥有长发的人士，那他们是位女士或男士的概率为？这是一个条件概率，P(man | long hair)，为我们已知晓的P(long hair | man)逆方式。因为条件概率不可逆，因此，我们对这个新条件概率知之甚少。

幸运的是托马斯观察到一些很酷炫的知识可以帮到我们。

根据联合概率计算规则，我们给出方程P(man with long hair)和P(long hair and man)。因为联合概率可逆，因此这两个方程等价。

借助一点代数知识，我们就能解出P(man | long hair)。

表达式采用A和B，替换“man”和“long hair”，于是我们得到贝叶斯定理。

我们回到最初，借助贝叶斯定理，解决电影院门票困境。

首先，需要计算边际概率P(long hair)。

接着代入数据，计算出长发中是男士的概率。对于男士休息室队列中的观影者而言，P(man | long hair)微微0.8。这让我们更加确信一直觉，掉门票的可能是一男士。贝叶斯定理抓住了在此情形下的直觉。更重要的是，更重要的是吸纳了先验知识，男士休息室外队列中男士远多于女士。借用此先验知识，更新我们对一这情形的认识。

概率分布

诸如影院困境这样的例子，很好地解释了贝叶斯推理的由来，以及作用机制。然而，在数据科学应用领域，此推理常常用于数据解释。有了我们测出来的先验知识，借助小数据集便可得出更好的结论。在开始细说之前，请先允许我先介绍点别的。就是我们需要清楚一个概率分布。

此处可以这样考虑概率，一壶咖啡正好装满一个杯子。倘若用一个杯子来装没有问题，那不止一个杯子呢，你需考虑如何将这些咖啡分这些杯子中。当然你可以按照自己的意愿，只要将所有咖啡放入某个杯子中。而在电影院，一个杯子或许代表女士或者男士。

或者我们用四个杯子代表性别和发长的所有组合分布。这两个案例中，总咖啡数量累加起来为一杯。

通常，我们将杯子挨个摆放，看其中的咖啡量就像一个柱状图。咖啡就像一种信仰，此概率分布用于显示我们相信某件事情的强烈程度。

假设我投了一块硬币，然后盖住它，你会认为正面和反面朝上的几率是一样的。

假设我投了一个骰子，然后盖住它，你会认为六个面中的每一个面朝上的几率是一样的。

假设我买了一期强力球彩票，你会认为中奖的可能性微乎其微。投硬币、投骰子、强力球彩票的结果，都可以视为收集、测量数据的例子。

毫无意外，你也可以对其它数据持有某种看法。这里我们考虑美国成年人的身高，倘若我告诉你，我见过，并测量了某些人的身高，那你对他们身高的看法，或许如上图所示。此观点认为一个人的身高可能介于150和200cm之间，最有可能的是介于180和190cm之间。

此分布可以分成更多的方格，视作将有限的咖啡放入更多的杯子，以期获得一组更加细颗粒度的观点。

最终虚拟的杯子数量将非常大，以至于这样的比喻变得不恰当。这样，分布变得连续。运用的数学方法可能有点变化，但底层的理念还是很有用。此图表明了你对某一事物认知的概率分布。

感谢你们这么有耐心！！有了对概率分布的介绍，我们便可采用贝叶斯定理进行数据解析了。为了说明这个，我以我家小狗称重为例。

兽医领域的贝叶斯推理

它叫雅各宾当政，每次我们去兽医诊所，它在秤上总是各种晃动，因此很难读取一个准确的数据。得到一个准确的体重数据很重要，这是因为，倘若它的体重有所上升，那么我们就得减少其食物的摄入量。它喜欢食物胜过它自己，所以说风险蛮大的。

最近一次，在它丧失耐心前，我们测了三次：13.9镑,17.5镑以及14.1镑。这是针对其所做的标准统计分析。计算这一组数字的均值，标准偏差，标准差，便可得到小狗当政的准确体重分布。

分布展示了我们认为的小狗体重，这是一个均值15.2镑，标准差1.2镑的正态分布。真实得测量如白线所示。不幸的是，这个曲线并非理想的宽度。尽管这个峰值为15.2镑，但概率分布显示，在13镑很容易就到达一个低值，在17镑到达一个高值。太过宽泛以致无法做出一个确信的决策。面对如此情形，通常的策略是返回并收集更多的数据，但在一些案例中此法操作性不强，或成本高昂。本例中，小狗当政的（Reign ）耐心已经耗尽，这是我们仅有的测量数据。

此时我们需要贝叶斯定理，帮助我们处理小规模数据集。在使用定理前，我们有必要重新回顾一下这个方程，查看每个术语。

我们用“w” (weight)和 “m” (measurements)替换“A” and “B” ，以便更清晰地表示我们如何用此定理。四个术语分别代表此过程的不同部分。

先验概率，P(w)，表示已有的事物认知。本例中，表示未称量时，我们认为的当政体重w。

似然值，P(m | w)，表示针对某个具体体重w所测的值m。又叫似然数据。

后验概率，P(w | m)，表示称量后，当政为某个体重w的概率。当然这是我们最感兴趣的。

译者注：后验概率，通常情况下，等于似然值乘以先验值。是我们对于世界的内在认知。

概率数据，P(m)，表示某个数据点被测到的概率。本例中，我们假定它为一个常量，且测量本身没有偏向。

对于完美的不可知论者来说，也不是什么特别糟糕的事情，而且无需对结果做出什么假设。例如本例中，即便假定当Reign的体重为13镑、或1镑，或1000000 镑，让数据说话。我们先假定一个均一的先验概率，即对所有值而言，概率分布就一常量值。贝叶斯定理便可简化为P(w | m) = P(m | w)。

此刻，借助Reign的每个可能体重，我们计算出三个测量的似然值。比如，倘若当政的体重为1000镑，极端的测量值是不太可能的。然而，倘若当政的体重为14镑或16镑。我们可以遍历所有，利用Reign的每一个假设体重值，计算出测量的似然值。这便是P(m | w)。得益于这个均一的先验概率，它等同于后验概率分布 P(w | m)。

这并非偶然。通过均值、标准偏差、标准差得来的，很像答案。实际上，它们是一样的，采用一个均一的先验概率给出传统的统计估测结果。峰值所在的曲线位置，均值，15.2镑也叫体重的极大似然估计（MLE）。

即使采用了贝叶斯定理，但依旧离有用的估计很远。为此，我们需要非均一先验概率。先验分布表示未测量情形下对某事物的认知。均一的先验概率认为每个可能的结果都是均等的，通常都很罕见。在测量时，对某些量已有些认识。年龄总是大于零，温度总是大于-276摄氏度。成年人身高罕有超过8英尺的。某些时候，我们拥有额外的领域知识，一些值很有可能出现在其它值中。

在Reign的案例中，我确实拥有其它的信息。我知道上次它在兽医诊所称到的体重是14.2镑。我还知道它并不是特别显胖或显瘦，即便我的胳膊对重量不是特别敏感。有鉴于此，它大概重14.2镑，相差一两镑上下。为此，我选用峰值为14.2镑。标准偏差为0.5镑的正态分布。

先验概率已经就绪，我们重复计算后验概率。为此，我们考虑某一概率，此时Reign体重为某一特定值，比如17镑。接着，17镑这一似然值乘以测量值为17这一条件概率。接着，对于其它可能的体重，我们重复这一过程。先验概率的作用是降低某些概率，扩大另一些概率。本例中，在区间13-15镑增加更多的测量值，以外的区间则减少更多的测量值。这与均一先验概率不同，给出一个恰当的概率，当政的真实体重为17镑。借助非均匀的先验概率，17镑掉入分布式的尾部。乘以此概率值使得体重为17镑的似然值变低。

通过计算当政每一个可能的体重概率，我们得到一个新的后验概率。后验概率分布的峰值也叫最大后验概率（MAP），本例为14.1镑。这和均一先验概率有明显的不同。此峰值更窄，有助于我们做出一个更可信的估测。现在来看，小狗当政的体重变化不大，它的体型依旧如前。

通过吸收已有的测量认知，我们可以做出一个更加准确的估测，其可信度高于其他方法。这有助于我们更好地使用小量数据集。先验概率赋予17.5镑的测量值是一个比较低的概率。这几乎等同于反对此偏离正常值的测量值。不同于直觉和常识的异常检测方式，贝叶斯定理有助于我们采用数学的方式进行异常检测。

另外，假定术语P(m)是均一的，但恰巧我们知道称量存在某种程度的偏好，这将反映在P(m)中。若称量仅输出某些数字，或返回读数2.0，占整个时间的百分之10，或第三次尝试产生一个随机测量值，均需要手动修改P(m)以反映这一现象，以便后验概率更加准确。

规避贝叶斯陷阱

探究Reign的真实体重体现了贝叶斯的优势。但这也存在某些陷阱。通过一些假设我们改进了估测，而测量某些事物的目的就是为了了解它。倘若我们假定对某一答案有所了解，我们可能会删改此数据。马克·吐温对强先验的危害做了简明地阐述，“将你陷入困境的不是你所不知道的，而是你知道的那些看似正确的东西。”

假如采取强先验假设，当Reign的体重在13与15镑之间，再假如其真实体重为12.5镑，我们将无法探测到。先验认知认为此结果的概率为零，不论做多少次测量，低于13镑的测量值都认为无效。

幸运的是，有一种两面下注的办法，可以规避这种盲目地删除。针对对于每一个结果至少赋予一个小的概率，倘若借助物理领域的一些奇思妙想，当政确实能称到1000镑，那我们收集的测量值也能反映在后验概率中。这也是正态分布作为先验概率的原因之一。此分布集中了我们对一小撮结果的大多数认识，不管怎么延展，其尾部再长都不会为零。

在此，红桃皇后是一个很好的榜样：

爱丽丝笑道：“试了也没用，没人会相信那些不存在的事情。”

“我敢说你没有太多的练习”，女王回应道，“我年轻的时候，一天中的一个半小时都在闭上眼睛，深呼吸。为何，那是因为有时在早饭前，我已经意识到存在六种不可能了。”来自刘易斯·卡罗尔的《爱丽丝漫游奇境》

重要朴素贝叶斯分类器详解及中文文本舆情分析（附代码实践）

本文主要讲述朴素贝叶斯分类算法并实现中文数据集的舆情分析案例，希望这篇文章对大家有所帮助，提供些思路。内容包括：

1.朴素贝叶斯数学原理知识

2.naive_bayes用法及简单案例

3.中文文本数据集预处理

4.朴素贝叶斯中文文本舆情分析

▌一. 朴素贝叶斯数学原理知识

该基础知识部分引用文章"机器学习之朴素贝叶斯(NB)分类算法与Python实现"（https://blog.csdn.net/moxigandashu/article/details/71480251），也强烈推荐大家阅读博主moxigandashu的文章，写得很好。同时作者也结合概率论讲解，提升下自己较差的数学。

朴素贝叶斯（Naive Bayesian）是基于贝叶斯定理和特征条件独立假设的分类方法，它通过特征计算分类的概率，选取概率大的情况，是基于概率论的一种机器学习分类（监督学习）方法，被广泛应用于情感分类领域的分类器。

下面简单回顾下概率论知识：

1.什么是基于概率论的方法？

通过概率来衡量事件发生的可能性。概率论和统计学是两个相反的概念，统计学是抽取部分样本统计来估算总体情况，而概率论是通过总体情况来估计单个事件或部分事情的发生情况。概率论需要已知数据去预测未知的事件。

例如，我们看到天气乌云密布，电闪雷鸣并阵阵狂风，在这样的天气特征(F)下，我们推断下雨的概率比不下雨的概率大，也就是p(下雨)>p(不下雨)，所以认为待会儿会下雨，这个从经验上看对概率进行判断。而气象局通过多年长期积累的数据，经过计算，今天下雨的概率p(下雨)=85%、p(不下雨)=15%，同样的 p(下雨)>p(不下雨)，因此今天的天气预报肯定预报下雨。这是通过一定的方法计算概率从而对下雨事件进行判断。

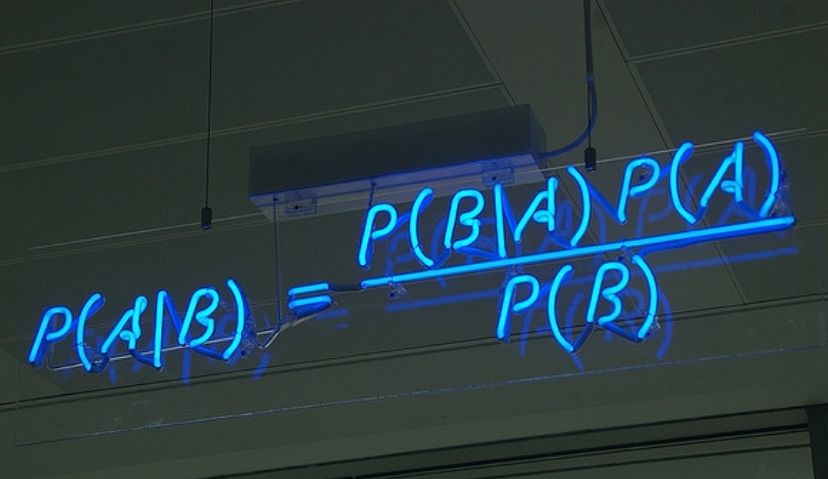
2.条件概率

若Ω是全集，A、B是其中的事件（子集），P表示事件发生的概率，则条件概率表示某个事件发生时另一个事件发生的概率。假设事件B发生后事件A发生的概率为：

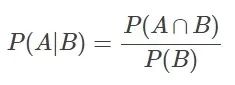
设P(A)>0，则有 P(AB) = P(B|A)P(A) = P(A|B)P(B)。

设A、B、C为事件，且P(AB)>0，则有 P(ABC) = P(A)P(B|A)P(C|AB)。

现在A和B是两个相互独立的事件，其相交概率为 P(A∩B) = P(A)P(B)。

3.全概率公式

设Ω为试验E的样本空间，A为E的事件，B1、B2、....、Bn为Ω的一个划分，且P(Bi)>0，其中i=1,2,...,n，则：

P(A) = P(AB1)+P(AB2)+...+P(ABn)

        = P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(Bn)

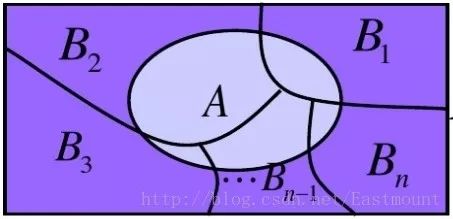
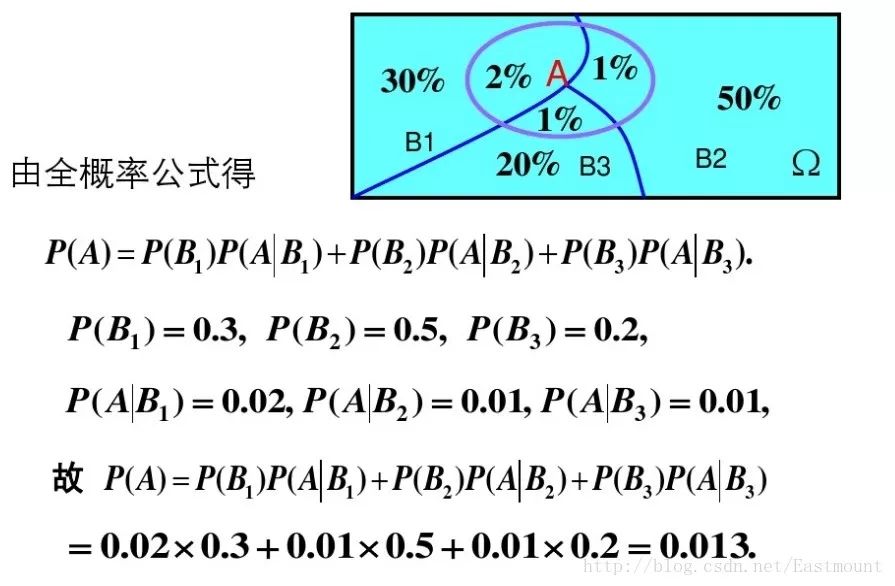
全概率公式主要用途在于它可以将一个复杂的概率计算问题，分解为若干个简单事件的概率计算问题，最后应用概率的可加性求出最终结果。

示例：有一批同一型号的产品，已知其中由一厂生成的占30%，二厂生成的占50%，三长生成的占20%，又知这三个厂的产品次品概率分别为2%、1%、1%，问这批产品中任取一件是次品的概率是多少？

参考百度文库资料：

https://wenku.baidu.com/view/05d0e30e856a561253d36fdb.html

4.贝叶斯公式

设Ω为试验E的样本空间，A为E的事件，如果有k个互斥且有穷个事件，即B1、B2、....、Bk为Ω的一个划分，且P(B1)+P(B2)+...+P(Bk)=1，P(Bi)>0（i=1,2,...,k)，则：

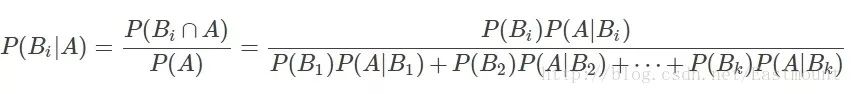
P(A)：事件A发生的概率；

P(A∩B)：事件A和事件B同时发生的概率；

P(A|B)：事件A在时间B发生的条件下发生的概率；

意义：现在已知时间A确实已经发生，若要估计它是由原因Bi所导致的概率，则可用Bayes公式求出。

5.先验概率和后验概率

先验概率是由以往的数据分析得到的概率，泛指一类事物发生的概率，根据历史资料或主观判断未经证实所确定的概率。后验概率而是在得到信息之后再重新加以修正的概率，是某个特定条件下一个具体事物发生的概率。

6.朴素贝叶斯分类

贝叶斯分类器通过预测一个对象属于某个类别的概率，再预测其类别，是基于贝叶斯定理而构成出来的。在处理大规模数据集时，贝叶斯分类器表现出较高的分类准确性。

假设存在两种分类：

  1) 如果p1(x,y)>p2(x,y)，那么分入类别1

  2) 如果p1(x,y)<p2(x,y)，那么分入类别2

引入贝叶斯定理即为：

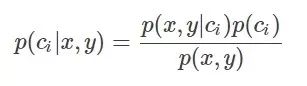
其中，x、y表示特征变量，ci表示分类，p(ci|x,y)表示在特征为x,y的情况下分入类别ci的概率，因此，结合条件概率和贝叶斯定理有：

  1) 如果p(c1|x,y)>p(c2,|x,y)，那么分类应当属于类别c1

  2) 如果p(c1|x,y)<p(c2,|x,y)，那么分类应当属于类别c2

贝叶斯定理最大的好处是可以用已知的概率去计算未知的概率，而如果仅仅是为了比较p(ci|x,y)和p(cj|x,y)的大小，只需要已知两个概率即可，分母相同，比较p(x,y|ci)p(ci)和p(x,y|cj)p(cj)即可。

7.示例讲解

假设存在14天的天气情况和是否能打网球，包括天气、气温、湿度、风等，现在给出新的一天天气情况，需要判断我们这一天可以打网球吗？首先统计出各种天气情况下打网球的概率，如下图所示。

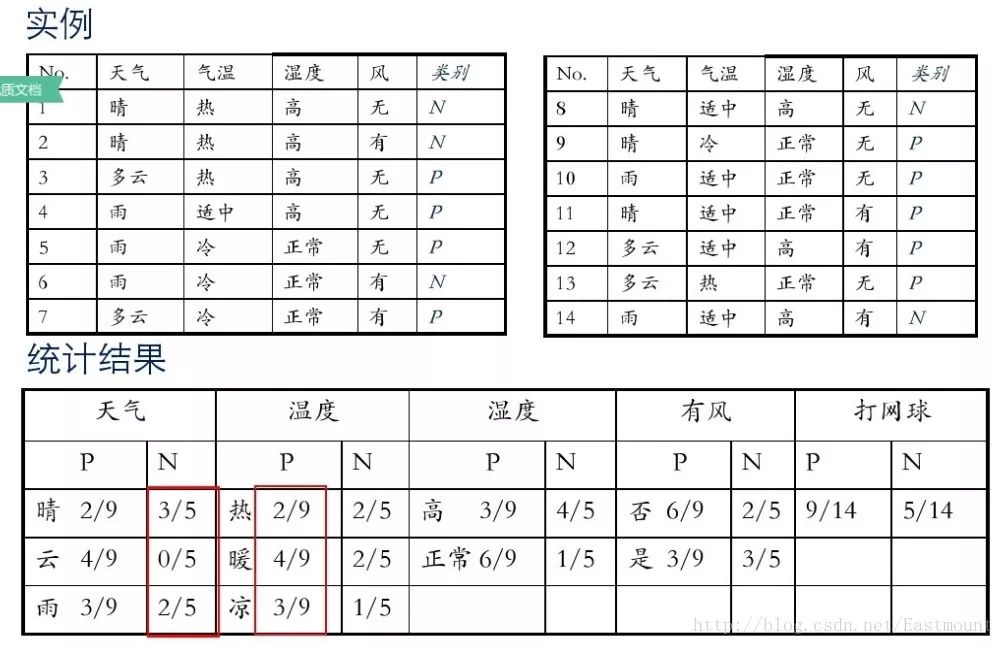
接下来是分析过程，其中包括打网球yse和不打网球no的计算方法。

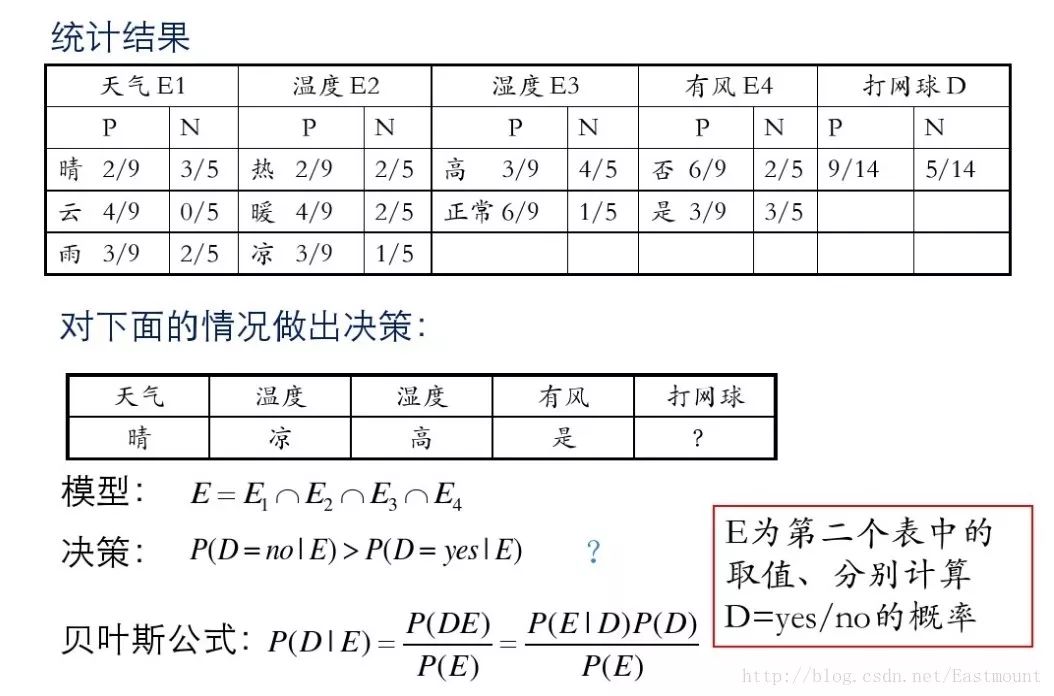
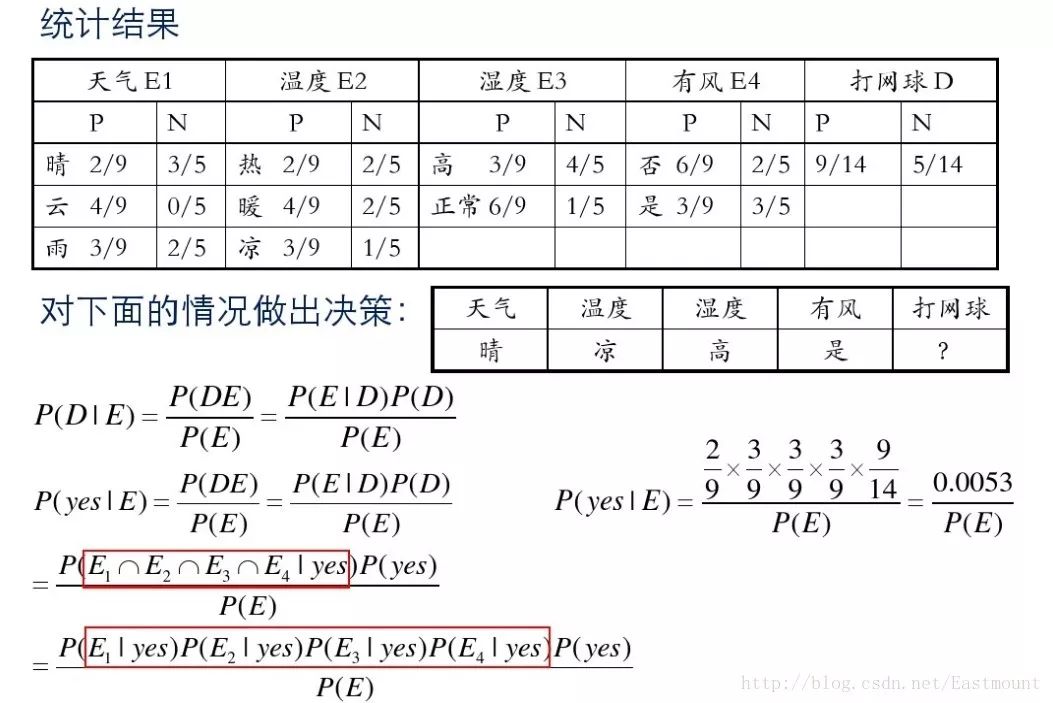
最后计算结果如下，不去打网球概率为79.5%。

8.优缺点

• 监督学习，需要确定分类的目标 

• 对缺失数据不敏感，在数据较少的情况下依然可以使用该方法

• 可以处理多个类别 的分类问题

• 适用于标称型数据 

• 对输入数据的形势比较敏感

• 由于用先验数据去预测分类，因此存在误差

▌二. naive_bayes用法及简单案例

scikit-learn机器学习包提供了3个朴素贝叶斯分类算法：

• GaussianNB(高斯朴素贝叶斯)

• MultinomialNB(多项式朴素贝叶斯)

• BernoulliNB(伯努利朴素贝叶斯)

1.高斯朴素贝叶斯

调用方法为：sklearn.naive_bayes.GaussianNB(priors=None)。

下面随机生成六个坐标点，其中x坐标和y坐标同为正数时对应类标为2，x坐标和y坐标同为负数时对应类标为1。通过高斯朴素贝叶斯分类分析的代码如下：

 1# -*- coding: utf-8 -*-
 2import numpy as np
 3from sklearn.naive_bayes import GaussianNB
 4X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
 5Y = np.array([1, 1, 1, 2, 2, 2])
 6clf = GaussianNB()
 7clf.fit(X, Y)      
 8pre = clf.predict(X)
 9print u"数据集预测结果:", pre
10print clf.predict([[-0.8, -1]])
11
12clf_pf = GaussianNB()
13clf_pf.partial_fit(X, Y, np.unique(Y)) #增加一部分样本
14print clf_pf.predict([[-0.8, -1]])

输出如下图所示，可以看到[-0.8, -1]预测结果为1类，即x坐标和y坐标同为负数。

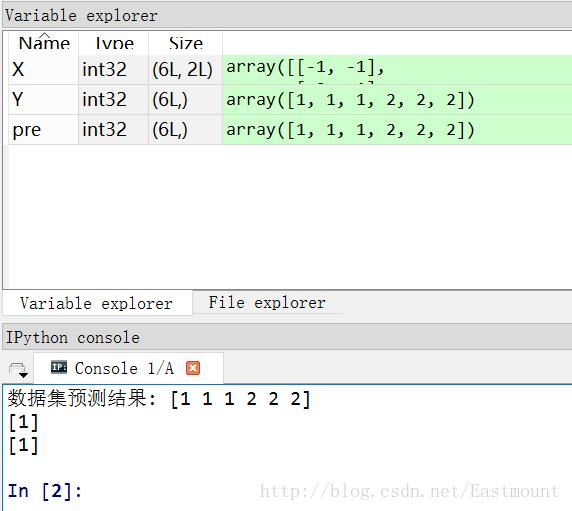
2.多项式朴素贝叶斯

多项式朴素贝叶斯：sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)主要用于离散特征分类，例如文本分类单词统计，以出现的次数作为特征值。

参数说明：alpha为可选项，默认1.0，添加拉普拉修/Lidstone平滑参数；fit_prior默认True，表示是否学习先验概率，参数为False表示所有类标记具有相同的先验概率；class_prior类似数组，数组大小为(n_classes,)，默认None，类先验概率。

3.伯努利朴素贝叶斯

伯努利朴素贝叶斯：sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True,class_prior=None)。类似于多项式朴素贝叶斯，也主要用于离散特征分类，和MultinomialNB的区别是：MultinomialNB以出现的次数为特征值，BernoulliNB为二进制或布尔型特性

下面是朴素贝叶斯算法常见的属性和方法。

1) class_prior_属性

观察各类标记对应的先验概率，主要是class_prior_属性，返回数组。代码如下：

1print clf.class_prior_
2#[ 0.5  0.5]

2) class_count_属性

获取各类标记对应的训练样本数，代码如下：

1print clf.class_count_
2#[ 3.  3.]

3) theta_属性

获取各个类标记在各个特征上的均值，代码如下：

1print clf.theta_
2#[[-2.         -1.33333333]
3# [ 2.          1.33333333]]

4) sigma_属性

获取各个类标记在各个特征上的方差，代码如下：

1print clf.theta_
2#[[-2.         -1.33333333]
3# [ 2.          1.33333333]]

5) fit(X, y, sample_weight=None)

训练样本，X表示特征向量，y类标记，sample_weight表各样本权重数组。

1#设置样本不同的权重
2clf.fit(X,Y,np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))
3print clf  
4print clf.theta_  
5print clf.sigma_ 

输出结果如下所示：

1GaussianNB()
2[[-2.25 -1.5 ]
3 [ 2.25  1.5 ]]
4[[ 0.6875  0.25  ]
5 [ 0.6875  0.25  ]]

6) partial_fit(X, y, classes=None, sample_weight=None)

增量式训练，当训练数据集数据量非常大，不能一次性全部载入内存时，可以将数据集划分若干份，重复调用partial_fit在线学习模型参数，在第一次调用partial_fit函数时，必须制定classes参数，在随后的调用可以忽略。

 1import numpy as np  
 2from sklearn.naive_bayes import GaussianNB  
 3X = np.array([[-1,-1], [-2,-2], [-3,-3], [-4,-4], [-5,-5], 
 4              [1,1], [2,2], [3,3]])  
 5y = np.array([1, 1, 1, 1, 1, 2, 2, 2])  
 6clf = GaussianNB()  
 7clf.partial_fit(X,y,classes=[1,2],
 8                sample_weight=np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))  
 9print clf.class_prior_ 
10print clf.predict([[-6,-6],[4,5],[2,5]])  
11print clf.predict_proba([[-6,-6],[4,5],[2,5]])

输出结果如下所示：

1[ 0.4  0.6]
2[1 2 2]
3[[  1.00000000e+00   4.21207358e-40]
4 [  1.12585521e-12   1.00000000e+00]
5 [  8.73474886e-11   1.00000000e+00]]

可以看到点[-6,-6]预测结果为1，[4,5]预测结果为2，[2,5]预测结果为2。同时，predict_proba(X)输出测试样本在各个类标记预测概率值。

7) score(X, y, sample_weight=None)

返回测试样本映射到指定类标记上的得分或准确率。

1pre = clf.predict([[-6,-6],[4,5],[2,5]])  
2print clf.score([[-6,-6],[4,5],[2,5]],pre)
3#1.0

最后给出一个高斯朴素贝叶斯算法分析小麦数据集案例，代码如下：

 1# -*- coding: utf-8 -*-
 2#第一部分 载入数据集
 3import pandas as pd
 4X = pd.read_csv("seed_x.csv")
 5Y = pd.read_csv("seed_y.csv")
 6print X
 7print Y
 8
 9#第二部分 导入模型
10from sklearn.naive_bayes import GaussianNB  
11clf = GaussianNB()
12clf.fit(X, Y)      
13pre = clf.predict(X)
14print u"数据集预测结果:", pre
15
16#第三部分 降维处理
17from sklearn.decomposition import PCA
18pca = PCA(n_components=2)
19newData = pca.fit_transform(X)
20print newData[:4]
21
22#第四部分 绘制图形
23import matplotlib.pyplot as plt
24L1 = [n[0] for n in newData]
25L2 = [n[1] for n in newData]
26plt.scatter(L1,L2,c=pre,s=200)
27plt.show()

输出如下图所示：

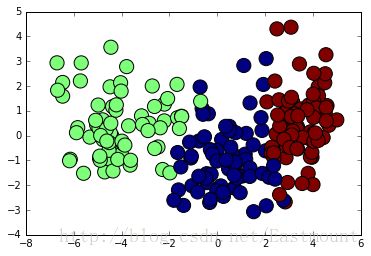
最后对数据集进行评估，主要调用sklearn.metrics类中classification_report函数实现的，代码如下：

1from sklearn.metrics import classification_report
2print(classification_report(Y, pre))

运行结果如下所示，准确率、召回率和F特征为91%。

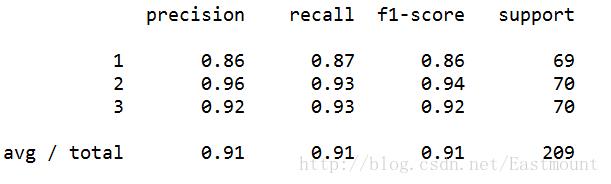
补充下Sklearn机器学习包常用的扩展类。

 1#监督学习
 2sklearn.neighbors #近邻算法
 3sklearn.svm #支持向量机
 4sklearn.kernel_ridge #核-岭回归
 5sklearn.discriminant_analysis #判别分析
 6sklearn.linear_model #广义线性模型
 7sklearn.ensemble #集成学习
 8sklearn.tree #决策树
 9sklearn.naive_bayes #朴素贝叶斯
10sklearn.cross_decomposition #交叉分解
11sklearn.gaussian_process #高斯过程
12sklearn.neural_network #神经网络
13sklearn.calibration #概率校准
14sklearn.isotonic #保守回归
15sklearn.feature_selection #特征选择
16sklearn.multiclass #多类多标签算法
17
18#无监督学习
19sklearn.decomposition #矩阵因子分解sklearn.cluster # 聚类
20sklearn.manifold # 流形学习
21sklearn.mixture # 高斯混合模型
22sklearn.neural_network # 无监督神经网络
23sklearn.covariance # 协方差估计
24
25#数据变换
26sklearn.feature_extraction # 特征提取sklearn.feature_selection # 特征选择
27sklearn.preprocessing # 预处理
28sklearn.random_projection # 随机投影
29sklearn.kernel_approximation # 核逼近

▌三. 中文文本数据集预处理

假设现在需要判断一封邮件是不是垃圾邮件，其步骤如下：

• 数据集拆分成单词，中文分词技术

• 计算句子中总共多少单词，确定词向量大小

• 句子中的单词转换成向量，BagofWordsVec

• 计算P(Ci)，P(Ci|w)=P(w|Ci)P(Ci)/P(w)，表示w特征出现时，该样本被分为Ci类的条件概率

• 判断P(w[i]C[0])和P(w[i]C[1])概率大小，两个集合中概率高的为分类类标

下面讲解一个具体的实例。

1.数据集读取

假设存在如下所示10条Python书籍订单评价信息，每条评价信息对应一个结果（好评和差评），如下图所示：

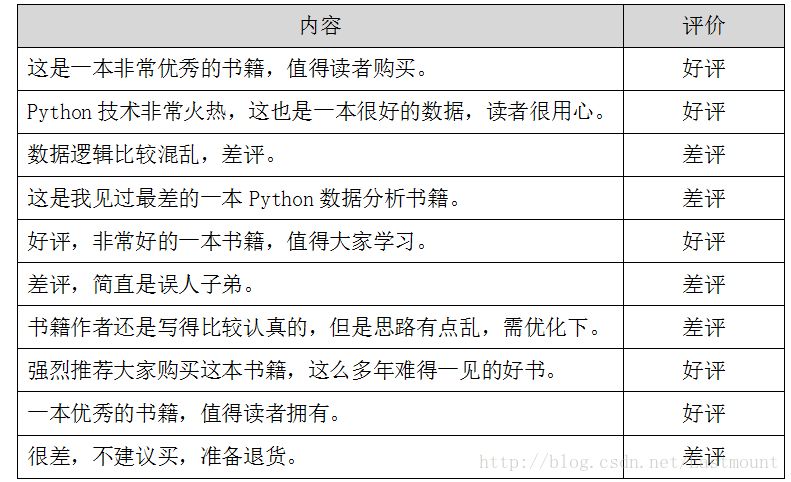
数据存储至CSV文件中，如下图所示。

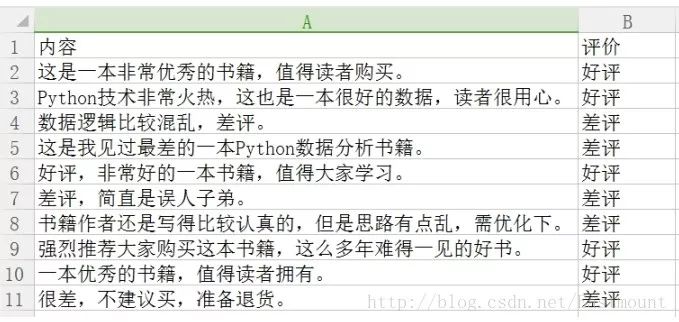
下面采用pandas扩展包读取数据集。代码如下所示：

 1# -*- coding: utf-8 -*-
 2import numpy as np
 3import pandas as pd
 4
 5data = pd.read_csv("data.csv",encoding='gbk')
 6print data
 7
 8#取表中的第1列的所有值
 9print u"获取第一列内容"
10col = data.iloc[:,0]  
11#取表中所有值  
12arrs = col.values
13for a in arrs:
14    print a

输出结果如下图所示，同时可以通过data.iloc[:,0]获取第一列的内容。

2.中文分词及过滤停用词

接下来作者采用jieba工具进行分词，并定义了停用词表，即：

stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])

完整代码如下所示：

 1# -*- coding: utf-8 -*-
 2import numpy as np
 3import pandas as pd
 4import jieba
 5
 6data = pd.read_csv("data.csv",encoding='gbk')
 7print data
 8
 9#取表中的第1列的所有值
10print u"获取第一列内容"
11col = data.iloc[:,0]  
12#取表中所有值  
13arrs = col.values
14#去除停用词  
15stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
16
17print u" 中文分词后结果:"
18for a in arrs:
19    #print a
20    seglist = jieba.cut(a,cut_all=False)     #精确模式  
21    final = ''
22    for seg in seglist:
23        seg = seg.encode('utf-8')
24        if seg not in stopwords: #不是停用词的保留
25            final += seg
26    seg_list = jieba.cut(final, cut_all=False) 
27    output = ' '.join(list(seg_list))         #空格拼接
28    print output

然后分词后的数据如下所示，可以看到标点符号及“这”、“我”等词已经过滤。

3.词频统计

接下来需要将分词后的语句转换为向量的形式，这里使用CountVectorizer实现转换为词频。如果需要转换为TF-IDF值可以使用TfidfTransformer类。词频统计完整代码如下所示：

 1# -*- coding: utf-8 -*-
 2import numpy as np
 3import pandas as pd
 4import jieba
 5
 6data = pd.read_csv("data.csv",encoding='gbk')
 7print data
 8
 9#取表中的第1列的所有值
10print u"获取第一列内容"
11col = data.iloc[:,0]  
12#取表中所有值  
13arrs = col.values
14#去除停用词  
15stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
16
17print u" 中文分词后结果:"
18corpus = []
19for a in arrs:
20    #print a
21    seglist = jieba.cut(a,cut_all=False)     #精确模式  
22    final = ''
23    for seg in seglist:
24        seg = seg.encode('utf-8')
25        if seg not in stopwords: #不是停用词的保留
26            final += seg
27    seg_list = jieba.cut(final, cut_all=False) 
28    output = ' '.join(list(seg_list))         #空格拼接
29    print output
30    corpus.append(output)
31
32#计算词频
33from sklearn.feature_extraction.text import CountVectorizer
34from sklearn.feature_extraction.text import TfidfTransformer
35
36vectorizer = CountVectorizer() #将文本中的词语转换为词频矩阵  
37X = vectorizer.fit_transform(corpus) #计算个词语出现的次数    
38word = vectorizer.get_feature_names() #获取词袋中所有文本关键词  
39for w in word: #查看词频结果
40    print w,
41print ''
42print X.toarray()  

输出结果如下所示，包括特征词及对应的10行数据的向量，这就将中文文本数据集转换为了数学向量的形式，接下来就是对应的数据分析了。

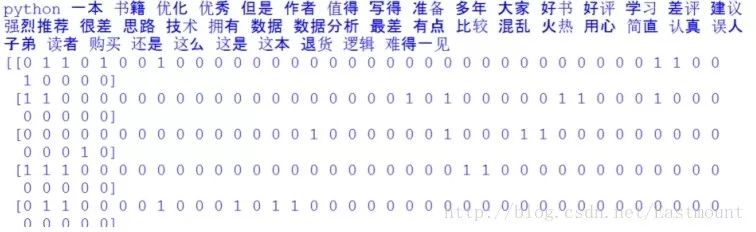
如下所示得到一个词频矩阵，每行数据集对应一个分类类标，可以预测新的文档属于哪一类。

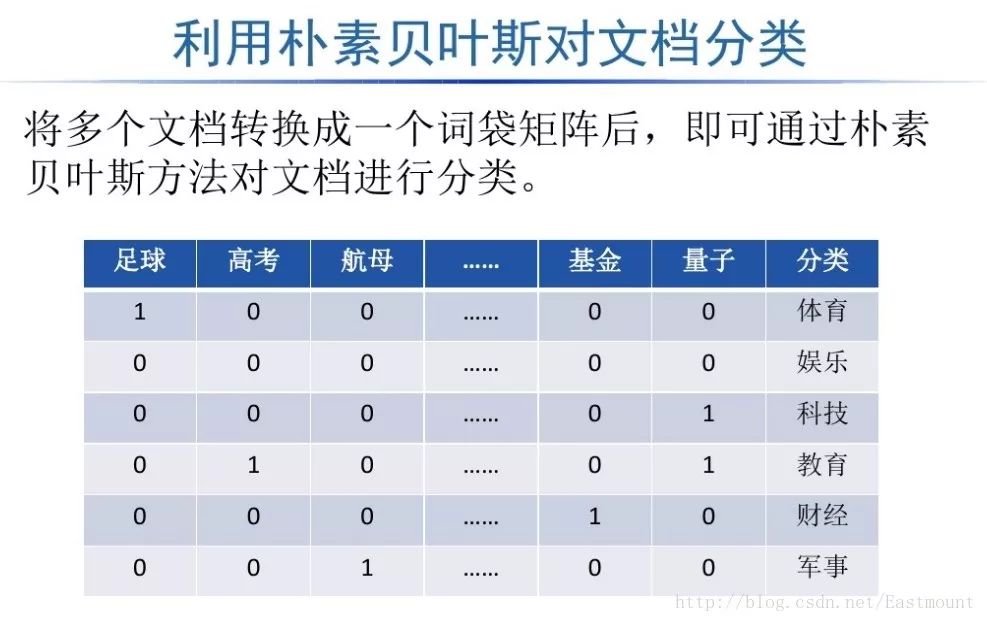
TF-IDF相关知识推荐我的文章： [python] 使用scikit-learn工具计算文本TF-IDF值（https://blog.csdn.net/eastmount/article/details/50323063）

▌四. 朴素贝叶斯中文文本舆情分析

最后给出朴素贝叶斯分类算法分析中文文本数据集的完整代码。

 1# -*- coding: utf-8 -*-
 2import numpy as np
 3import pandas as pd
 4import jieba
 5
 6#http://blog.csdn.net/eastmount/article/details/50323063
 7#http://blog.csdn.net/eastmount/article/details/50256163
 8#http://blog.csdn.net/lsldd/article/details/41542107
 9
10####################################
11#         第一步 读取数据及分词
12#
13data = pd.read_csv("data.csv",encoding='gbk')
14print data
15
16#取表中的第1列的所有值
17print u"获取第一列内容"
18col = data.iloc[:,0]  
19#取表中所有值  
20arrs = col.values
21
22#去除停用词  
23stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
24
25print u" 中文分词后结果:"
26corpus = []
27for a in arrs:
28    #print a
29    seglist = jieba.cut(a,cut_all=False)     #精确模式  
30    final = ''
31    for seg in seglist:
32        seg = seg.encode('utf-8')
33        if seg not in stopwords: #不是停用词的保留
34            final += seg
35    seg_list = jieba.cut(final, cut_all=False) 
36    output = ' '.join(list(seg_list))         #空格拼接
37    print output
38    corpus.append(output)
39
40####################################
41#         第二步 计算词频
42#
43from sklearn.feature_extraction.text import CountVectorizer
44from sklearn.feature_extraction.text import TfidfTransformer
45
46vectorizer = CountVectorizer() #将文本中的词语转换为词频矩阵  
47X = vectorizer.fit_transform(corpus) #计算个词语出现的次数    
48word = vectorizer.get_feature_names() #获取词袋中所有文本关键词  
49for w in word: #查看词频结果
50    print w,
51print ''
52print X.toarray()  
53
54
55####################################
56#         第三步 数据分析
57#
58from sklearn.naive_bayes import MultinomialNB  
59from sklearn.metrics import precision_recall_curve  
60from sklearn.metrics import classification_report
61
62#使用前8行数据集进行训练，最后两行数据集用于预测
63print u" 数据分析:"
64X = X.toarray()
65x_train = X[:8]
66x_test = X[8:]
67#1表示好评 0表示差评
68y_train = [1,1,0,0,1,0,0,1]
69y_test = [1,0]
70
71#调用MultinomialNB分类器  
72clf = MultinomialNB().fit(x_train, y_train)
73pre = clf.predict(x_test)
74print u"预测结果:",pre
75print u"真实结果:",y_test
76
77from sklearn.metrics import classification_report
78print(classification_report(y_test, pre))

输出结果如下所示，可以看到预测的两个值都是正确的。即“一本优秀的书籍，值得读者拥有。”预测结果为好评（类标1），“很差，不建议买，准备退货。”结果为差评（类标0）。

1数据分析:
2预测结果: [1 0]
3真实结果: [1, 0]
4             precision    recall  f1-score   support
5
6          0       1.00      1.00      1.00         1
7          1       1.00      1.00      1.00         1
8
9avg / total       1.00      1.00      1.00         2

但存在一个问题，由于数据量较小不具备代表性，而真实分析中会使用海量数据进行舆情分析，预测结果肯定页不是100%的正确，但是需要让实验结果尽可能的好。最后补充一段降维绘制图形的代码，如下：

 1#降维绘制图形
 2from sklearn.decomposition import PCA
 3pca = PCA(n_components=2)
 4newData = pca.fit_transform(X)
 5print newData
 6
 7pre = clf.predict(X)
 8Y = [1,1,0,0,1,0,0,1,1,0]
 9import matplotlib.pyplot as plt
10L1 = [n[0] for n in newData]
11L2 = [n[1] for n in newData]
12plt.scatter(L1,L2,c=pre,s=200)
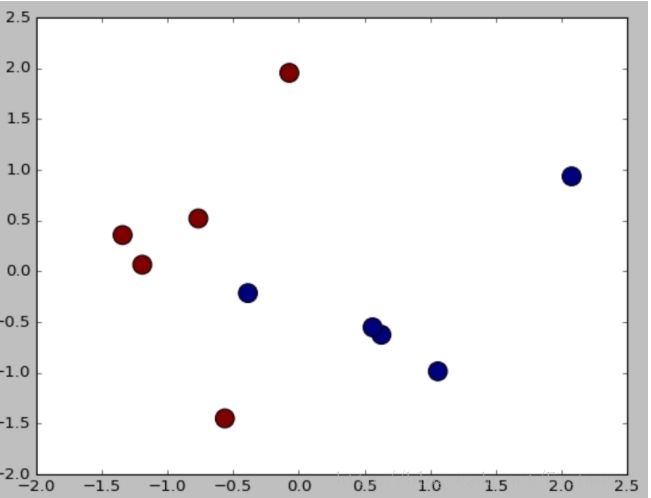
13plt.show()

输出结果如图所示，预测结果和真实结果都是一样的，即[1,1,0,0,1,0,0,1,1,0]。

往期 精彩回顾

     

         

                           。

 

 

                   。

 

 

                   。

 

 

                   。

 

 

 

                   。 

END

        关注步骤：

                1、长按下图二秒。

                2、弹出下图，请选择“识别图中二维码”

                          

                3、选择关注即可。

        要想了解更多人工智能、区块链、大数据、云计算相关资讯，行业动态，行业报告，开发资料等，请点击“阅读原文”。