如何判别测量数据中是不是有异常值

Posted 2023-04-23

　　
　　异常值outlier：指样本中的个别值，其数值明显偏离它（或他们）所属样本的其余观测值,也称异常数据，离群值。
　　
　　目前人们对异常值的判别与剔除主要采用物理判别法和统计判别法两种方法。
　　
　　所谓物理判别法就是根据人们对客观事物已有的认识，判别由于外界干扰、人为误差等原因造成实测数据值偏离正常结果，在实验过程中随时判断，随时剔除。
　　
　　统计判别法是给定一个置信概率，并确定一个置信限，凡超过此限的误差，就认为它不属于随机误差范围，将其视为异常值剔除。当物理识别不易判断时，一般采用统计识别法。
　　
　　对于多次重复测定的数据值，异常值常用的统计识别与剔除法有：
　　
　　拉依达准则法（3δ）：简单，无需查表。测量次数较多或要求不高时用。是最常用的异常值判定与剔除准则。但当测量次数《=10次时，该准则失效。
　　
　　如果实验数据值的总体x是服从正态分布的，则

　　式中，μ与σ分别表示正态总体的数学期望和标准差。此时，在实验数据值中出现大于μ＋3σ或小于μ—3σ数据值的概率是很小的。因此，根据上式对于大于μ＋3σ或小于μ—3σ的实验数据值作为异常值，予以剔除。具体计算方法参见http://202.121.199.249/foundrymate/lessons/data-analysis/13/131.htm
　　在这种情况下，异常值是指一组测定值中与平均值的偏差超过两倍标准差的测定值。与平均值的偏差超过三倍标准差的测定值，称为高度异常的异常值。在处理数据时，应剔除高度异常的异常值。异常值是否剔除，视具体情况而定。在统计检验时，指定为检出异常值的显著性水平α=0.05，称为检出水平；指定为检出高度异常的异常值的显著性水平α=0.01，称为舍弃水平，又称剔除水平(reject level)。
　　标准化数值（Z-score）可用来帮助识别异常值。Z分数标准化后的数据服从正态分布。因此，应用Z分数可识别异常值。我们建议将Z分数低于-3或高于3的数据看成是异常值。这些数据的准确性要复查，以决定它是否属于该数据集。
　　
　　肖维勒准则法（Chauvenet）：经典方法，改善了拉依达准则，过去应用较多，但它没有固定的概率意义，特别是当测量数据值n无穷大时失效。
　　狄克逊准则法（Dixon）：对数据值中只存在一个异常值时，效果良好。担当异常值不止一个且出现在同侧时，检验效果不好。尤其同侧的异常值较接近时效果更差，易遭受到屏蔽效应。
　　罗马诺夫斯基（t检验）准则法：计算较为复杂。
　　格拉布斯准则法（Grubbs）：和狄克逊法均给出了严格的结果，但存在狄克逊法同样的缺陷。朱宏等人采用数据值的中位数取代平均值，改进得到了更为稳健的处理方法。有效消除了同侧异常值的屏蔽效应。国际上常推荐采用格拉布斯准则法。
　　 参考技术A 在回弹法检测砼强度中，按批抽样检测的测区数量往往很多，这就不可避免出现较多的检测异常值，怎样判断和处理这些异常值，对于提高检测结果的准确性意义重大。格拉布斯检验法是土木工程中常用的一种检验异常值的方法，其应用于回弹法检测砼强度，能有效提高按批抽样检测结果的准确性。本回答被提问者和网友采纳 参考技术B 可以通过闭合差检核和重复观测的较差来判断。

测试中的异常数据剔除用啥方法？

测试中的异常数据剔除用什么方法？如题，常用方法，便于使用的方法！

统计学中剔除异常数据的方法很多，但在检测和测试中经常用的方法有2种：

1- 拉依达准则(也称之为3σ准则)：

很简单，就是首先求得n次独立检测结果的实验标准差s和残差，│残差│大于3s的测量值即为异常值删去，然后重新反复计算，将所有异常值剔除。

但这个方法有局限，数据样本必须大于10，一般要求大于50。所以，这个方法现在不常用了，国标里面已经剔除该方法！

2- 格拉布斯准则（Grubbs）：

这个方法比较常用，尤其是我们检测领域。

方法也很简单，还是首先求得n次独立检测结果的实验标准差s和残差，│残差│/s的值大于  g(n)的测量值即为异常值，可删去；同样重新反复计算之，将所有异常值剔除。

g(n)指 临界系数,可直接查表获得. 95%的系数可参见下表：

参考技术A

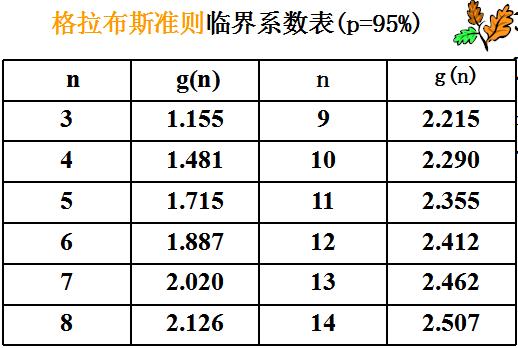
处理异常值

异常值的定义是与均值的偏差超过两倍标准，但是在脏数据中，异常值的情况不止这一种：

1）比如一列数据你打开看全部是数字，当你把它当数值型处理，它会报错；那就得仔细查找原因，遇到比较多的情况是一列数字中夹杂了几个奇怪的字符串或者符号等元素，如果几万条数据中只有一两个这种字符，即使认真从前到后仔细查看也很难发现还浪费大量时间，效率极低。

还有一种情况比较常见，就是看起来是数字，实际上都是字符串的形式，但是以表格查看的时候是看不到字符串的引号；这两种情况可以通过查看特征类型来提前发现，在python中用type()或者dtypes()函数，两者使用对象有差别，可自行了解；

2）几种常用异常值检测方法：

3σ探测方法

3σ探测方法的思想其实就是来源于切比雪夫不等式。

对于任意ε>0，有：

当时，如果总体为一般总体的时候，统计数据与平均值的离散程度可以由其标准差反映，因此有：

一般所有数据中，至少有3/4（或75%）的数据位于平均2个标准差范围内。

所有数据中，至少有8/9（或88.9%）的数据位于平均数3个标准差范围内。

所有数据中，至少有24/25（或96%)的数据位于平均数5个标准差范围内。


所以如果我们一般是把超过三个离散值的数据称之为异常值。这个方法在实际应用中很方便的使用，但是他只有在单个属性的情况下才适用。

z-score


Z-score是一维或低维特征空中的参数异常检测方法。该技术假定数据是高斯分，异常值是分布尾部的数据点，因此远离数据的平均值。距离的远近取决于使用公式计算的归一化数点z i的设定阈值Zthr：



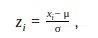
其中xi是一个数据点，μ是所有点xi的平均值，δ是所有点xi的标准偏。
然后经过标准化处理后，异常值也进行标准化处理，其绝对值大于Zthr：



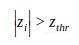
Zthr值一般设置为2.5、3.0和3.5。该技术是使用KNIME工作流中的行过滤器节点实现的。

这种异常值处理需要结合最终需求来决定怎么处理，常见的是不处理或者按缺失值的方法处理，但是在实际场景中，异常值有时候会有非常突出的表现，比如在现金贷业务中，异常值中的坏账率远高于整体坏账水平或其他区间坏账水平，这时候异常值就得保留并作为决策阈值的参考值。

IQR

观察箱型图，或者通过IQR（InterQuartile Range）计算可以得到数据分布的第一和第四分位数，异常值是位于四分位数范围之外的数据点。

这个方法真的很简单，因为只需要给数据排个序就行了，显然过于笼统，但在实际场景中，观察箱型图仍然是一个很好的探索数据分布的方法。

毕竟，所有复杂的探索，都是从最开始简单的探索一步步得来的嘛！