异常检测统计学方法

Posted 2023-04-18

参考技术A

1. 概述
2. 参数方法

3. 非参数方法
4. HBOS
5. 总结

<span id="1"></span>

统计学方法对数据的正常性做出假定。 它们假定正常的数据对象由一个统计模型产生，而不遵守该模型的数据是异常点。 统计学方法的有效性高度依赖于对给定数据所做的统计模型假定是否成立。

具体方法：先基于统计学方法确定一个概率分布模型，然后判断各个离散点有多大概率符合该模型。

难点在于如何得到概率分布模型。首先是识别数据集的具体分布：数据的真实分布是否是现在手里的数据集完全体现的。尽管许多类型的数据都可以用常见的分布（高斯分布、泊松分布或者二项式分布）来描述，但是具有非标准分布的数据集非常常见。如果选择了错误的模型，则对象可能会被错误地识别为异常点。其次，如何确定使用属性的个数，基于统计学的方法，数据的属性一般具有一个或多个，那么在建立概率分布模型的过程中究竟是用一个属性还是多个属性需要分析和尝试。最后，当使用数据属性很多时，模型比较复杂并且难以理解，会涉及到EM算法。

异常检测的统计学方法，有两种具体的方法：参数方法和非参数方法。

<span id="2"></span>

假定正常的数据对象被一个以 为参数的参数分布产生。该参数分布的概率密度函数 给出对象 被该分布产生的概率。该值越小， 越可能是异常点。

<span id="2.1"></span>

仅涉及一个属性或变量的数据称为一元数据。我们假定数据分布符合正态分布，然后通过现有的数据得到正态分布的关键参数，把低概率的点识别为异常点。

假定输入的数据集为 ，数据集中的样本服从正态分布，即存在一个 和 ，使得 。这里的 和 可以通过计算求得。

计算公式如下：

求出上述的参数后，我们就可以根据概率密度函数计算每个数据点服从正态分布的概率，或者说离散数据点的概率。

概率计算公式为：

需要确定一个阈值，这个阈值一般是经验值，可以选择在验证集上使得评估指标值最大的阈值取值作为最终阈值。如果计算出来的概率低于阈值，就可以认为该数据点为异常点。

例如常用的3sigma原则，如果数据点超过范围 ，那么这些点可能是异常点。

这个方法还可以用于可视化。参考箱型图，以数据集的上下四分位数（Q1和Q3）、中点等参数，异常点常被定义为小于 和 。其中， 。

利用python画一个箱型图：

<span id="2.2"></span>

涉及两个或多个属性或变量的数据称为多元数据。分为两种情况，一种是特征相互独立，一种是特征间不相互独立。

<span id="2.2"></span>

当数据是多元数据的时候，核心思想是把多元异常点检测任务转换为一元异常点检测问题。例如基于正态分布的一元异常点检测扩充到多元情形时，可以求出每一维度的均值和标准差。对于第 维：

计算概率密度函数：

<span id="2.2.2"></span>

<span id="2.3"></span>

当实际数据很复杂时，可以考虑建立混合参数模型，假定数据集 包含来自两个概率分布： 是大多数（正常）对象的分布，而 是异常对象的分布。数据的总概率分布可以记作

其中， 是一个数据对象； 是0和1之间的数，给出离群点的期望比例。

<span id="3"></span>

相比参数方法，非参数方法对数据做较少的假定，不做先验概率分布，因而在更多情况下被使用。

直方图是一种频繁使用的非参数统计模型，可以用来检测异常点。该过程包括如下两步：

步骤1：构造直方图。使用输入数据（训练数据）构造一个直方图。该直方图可以是一元的，或者多元的（如果输入数据是多维的）。

尽管非参数方法并不假定任何先验统计模型，但是通常确实要求用户提供参数，以便由数据学习。例如，用户必须指定直方图的类型（等宽的或等深的）和其他参数（直方图中的箱数或每个箱的大小等）。与参数方法不同，这些参数并不指定数据分布的类型。

步骤2：检测异常点。为了确定一个对象是否是异常点，可以对照直方图检查它。在最简单的方法中，如果该对象落入直方图的一个箱中，则该对象被看作正常的，否则被认为是异常点。

对于更复杂的方法，可以使用直方图赋予每个对象一个异常点得分。例如令对象的异常点得分为该对象落入的箱的容积的倒数。

使用直方图作为异常点检测的非参数模型的一个缺点是， 很难选择一个合适的箱尺寸 。一方面，如果箱尺寸太小，则许多正常对象都会落入空的或稀疏的箱中，因而被误识别为异常点。另一方面，如果箱尺寸太大，则异常点对象可能渗入某些频繁的箱中，因而“假扮”成正常的。

<span id="4"></span>

HBOS全名为：Histogram-based Outlier Score。它是一种单变量方法的组合，不能对特征之间的依赖关系进行建模，但是计算速度较快，对大数据集友好。其基本假设是数据集的每个维度 相互独立 。然后对每个维度进行区间(bin)划分，区间的密度越高，异常评分越低。

HBOS算法流程：

推导过程如下：

<span id="5"></span>

异常检测 -- Kibana5.4时间序列分析

1

一个复杂的系统在许多方面都可能出现问题，这些问题可简单分为两类：一类是可以预料到的问题，比如磁盘失败，这种问题会重复发生并且可以被直接验证；另一类是无法预期的——本文主要是针对这类问题展开。 

应对这种无法预期的问题，一个有效的工具就是统计学。用统计学的方法检测到异常点然后触发报警是我们的异常检测系统所做的工作。统计学的强大之处在于能够捕捉到新出现的问题；而不足之处是需要进一步跟踪和查询到问题根源。 

建立一个有效的异常检测器最大的挑战是如何减少误报。如果一个报警系统存在很多误报，用户的通常做法就是将它关闭，或者将报警扔到垃圾箱，更常见的就是直接忽略这些报警，那这样的报警系统就没有太大的存在意义。

2

eBay所使用的方法就是基于统计学的异常检测。我们的查询系统中的监控信号是基于定时发布的参考查询结果得到的。系统需要先将这些监控信号进行编码得到一些数字集合——这项通过对查询结果进行指标的计算实现。对于每次查询，都可以计算50个左右相关的指标来对查询结果做归纳总结。比如某次查询结果集中物品的数量，查询结果集里所有物品价格的中位数，这就是2个不同的指标。我们有3000个参考查询，每个都可计算50个指标，所以就会产生150,000个指标；现在参考查询定时每4个小时发布一次，因此一天会产生900,000个指标。对于现在TB级别的数据库来说这个量是很小的，问题是如何从这么多数据中筛选出异常值，并且尽可能避免误报。 

下图是一次发布的参考查询和每个多对应的指标图： 

3

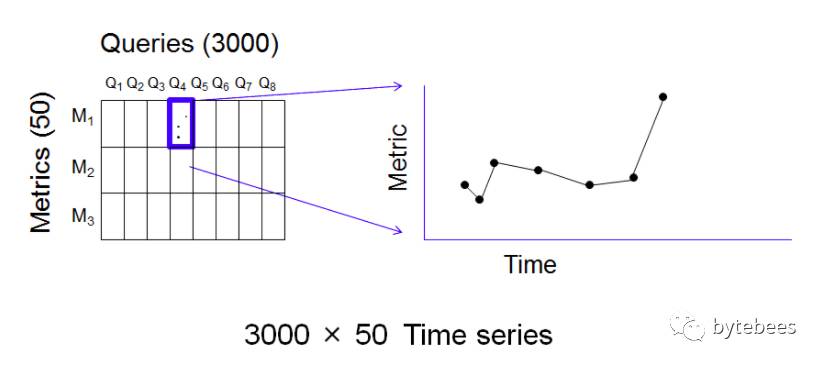
每一对(query,metric)都是一个随时间变化的数字，所以可以由查询q和指标m确定一个时间序列。因此每个时间窗（这里是4个小时）有150,000个时间序列生成。这么多的时间序列偶然出现一个异常报警是极有可能的，所以对每个时间序列分别进行监控报警是不现实的，将产生过多误报。

我们的解决方案就是聚合，想法很简单：检查每个时间序列并计算最近一个点的实际值和期望值（期望值是由历史值计算得到）之差——这个差值称为“意外”(surprise)。所以对每个查询q和指标m，在任意一个时间点t处就有一个意外值： 

4

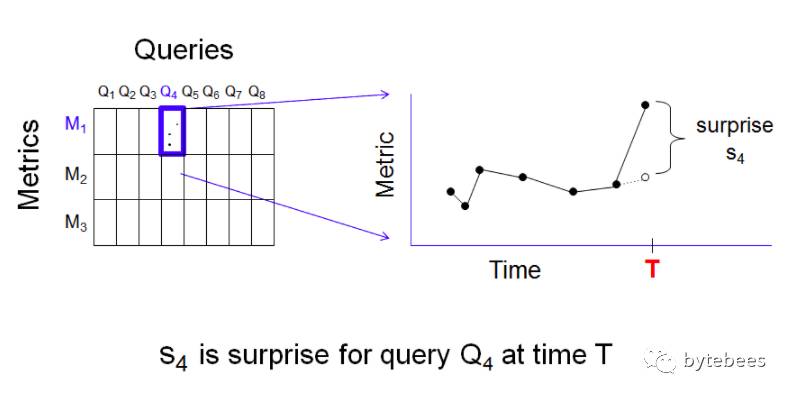
异常检测的思路是：固定一个时间点T，期望只有少数几个(q,m,T)存在较大的意外；假如出现了多个较大的意外值，就认为是异常需要进行报警。为了将这种方法量化，固定一个指标m，对所有3000个查询计算意外值，并算出这些意外值在时间T处的90百分位数S90(T)：

5

由此每个指标所有查询的90百分位数构成了一个新的时间序列。假设两个指标的S90时间序列如下：

6

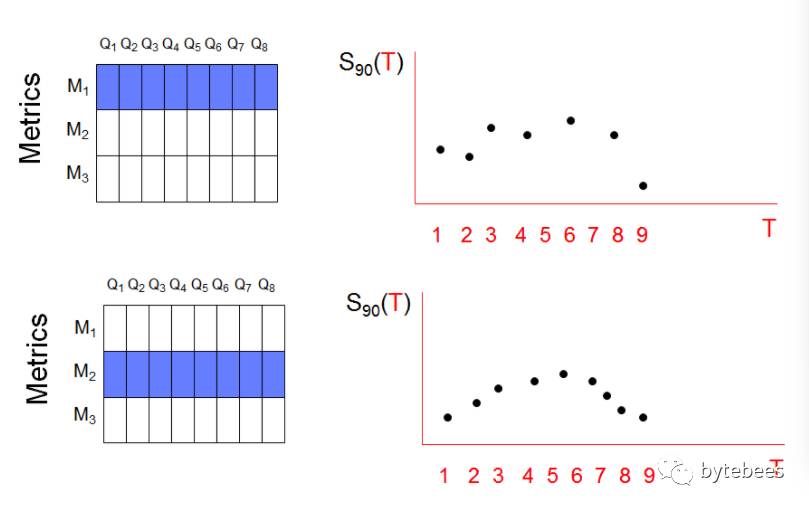
至此，我们将原先的150,000个时间序列减少到了50个。这种聚合手段对于异常检测是十分有效的。我们在这种时间序列的聚合方法基础上做简单的统计：计算最终得到的50个序列的均值avg和方差σ，如果一个序列值大于avg+3σ则认为是异常值。