pca算法介绍及简单实例

Posted 2023-04-12

参考技术A 主成分分析（Principal components analysis，PCA）是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数，同时保持数据集中的对方差贡献最大的特征。

简而言之，PCA就是压缩数据，降低维度，把重要的特征留下来。

目的:

当你有上百上千个特征，它们可能来自不同的部门给的数据，可能这些来自不同的数据是可以互相推导的，或者某个特征是对结果没什么影响的，或者来自不同的部门的数据其实在描述同一个问题，那么这些冗余的特征是没有价值的。

我们可以通过降低维度（用机器学习的话来说就是去掉一些特征）来提高算法效率。

在解决机器学习问题时，如果能把数据可视化，可以大大帮助我们找到解决方案。但是，如果特征太多（即维数太多），你很难画出图，就算画出来了也不容易理解。

我们可以通过降低维度使数据反映在平面或者立体空间中，便于数据分析

对于一组数据，如果它在某一坐标轴上的方差越大，说明坐标点越分散，该属性能够比较好的反映源数据。所以在进行降维的时候，主要目的是找到一个超平面，它能使得数据点的分布方差呈最大，这样数据表现在新的坐标轴上时候已经足够分散了。

我们要对数据样本进行中心化，中心化即是指变量减去它的均值。我们通过坐标轴变换，使得原本属于x轴的数据样本变成w轴样本。我们希望变化后的数据在坐标轴w的呈现的值z的方差最大，则我们会得到图示目标函数，并且由于w是坐标轴，所以我们会得到一个约束条件。根据拉格朗日乘子法可以解决该问题，经过处理后我们把问题变成了x协方差求特征值，求特征向量的问题了。

我们已经在上述过程中知道了问题的数学模型，我们可以解除p个特征值与对应的特征向量。我们可以对特征值进行大到小排序，如果我们要从p维 --> q维（q＜p），那么我们只需要取前q个特征值对应的特征向量进行向量相乘。如果问题并没有给出具体q的值，那么我们可以通过计算如下式子便可以知道q的取值。其中t的取值相当于是一个阈值，比如我们需要保留80%，那么t=0.8即可。

（1）假设我们有一个二维数据，我们要通过PCA的方法来将这个二维数据降到一维。

（2）因为数据已经中心化，所以我们就省去了中心化的步骤。我们开始求x协方差。

先来看看协方差的定义和计算方式。

计算结果如下

同样的，了解一下特征值和特征向量的定义以及计算方式

以此题为例，分两步来做

a.由矩阵A的特征方程求特征值

b.把每个特征值代入线性方程组，求出基础解系。（打不出来莱姆达我也很难受）

结果如下

⑥将二维变成一维，选择最大的特征值和对应的特征向量进行降维，结果如下

Python实例PCA算法实现

目录

• 作者介绍
• PCA算法介绍
• 数据集介绍
• 代码实现
• 降维结果
• Reference

作者介绍

王世豪，男，西安工程大学电子信息学院，2020级硕士研究生，张宏伟人工智能课题组。
研究方向：机器视觉与人工智能。
电子邮件：[e-mail]

PCA算法介绍

PCA（Principal Component Analysis，主成分分析）是一种多变量统计方法，它是最常用的降维方法之一，通过正交变换将一组可能存在相关性的变量数据转换为一组线性不相关的变量，转换后的变量被称为主成分。
原理可参考PCA原理详解。

数据集介绍

Iris鸢尾花数据集是一个经典的多重变量分析的数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含3类共150条记录，每类各50个数据，每条记录都有4项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的哪一品种。

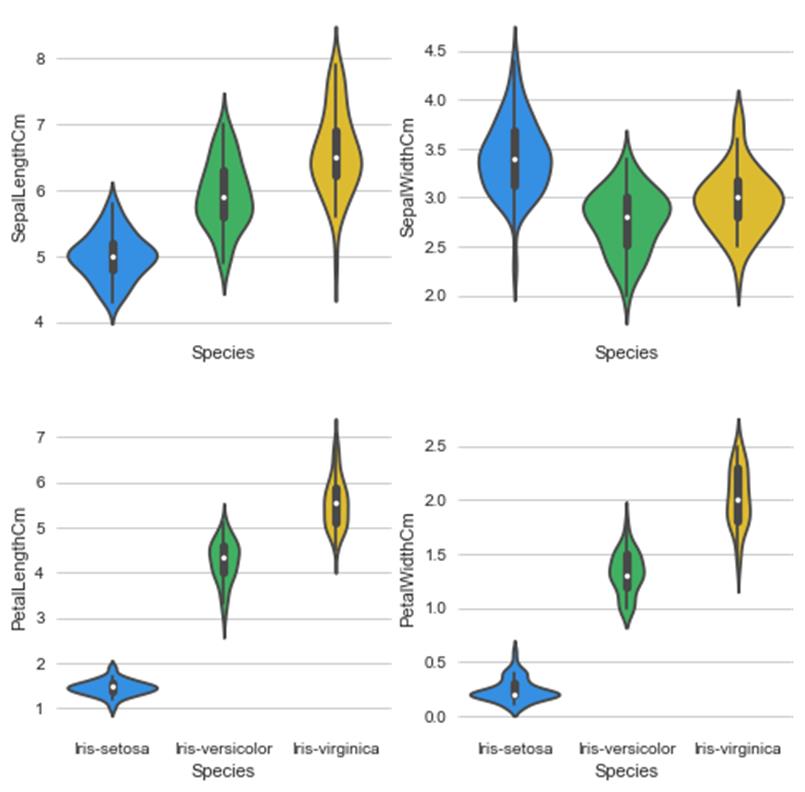
在程序中我们直接从sklearn库中调取数据集，所以不需要提前进行下载。

代码实现

先在之前创建的虚拟环境中安装sklearn和matplotlib库，之后调用Python解释器就可以在Pycharm中实现PCA了。

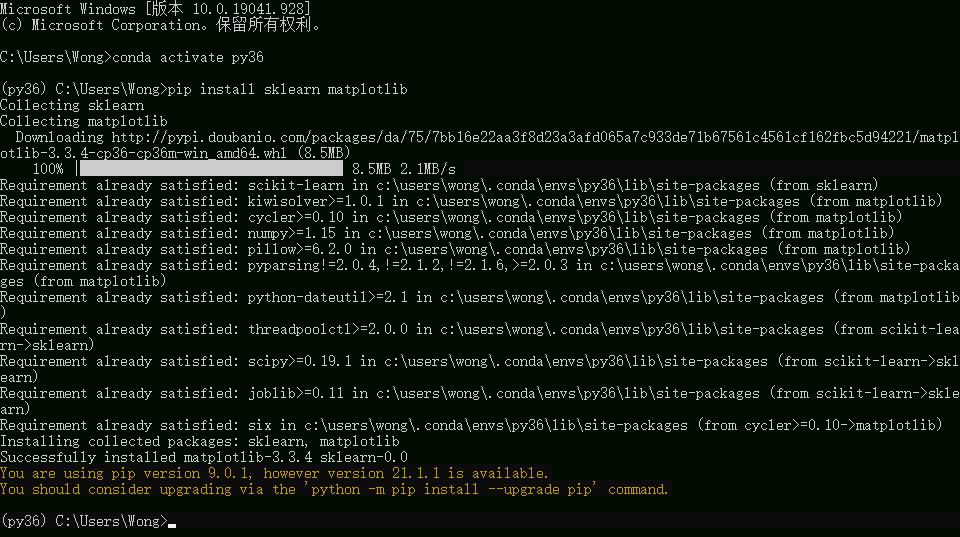
注意：代码是需要在安装好的Pycharm中运行，或者任一IDE均可，不是在终端（命令行窗口）。

# -*- coding:utf-8 -*-
# 导入鸢尾花数据集，调用matplotlib包用于数据的可视化，并加载PCA算法包。
import matplotlib.pyplot as plt                
from sklearn.decomposition import PCA          
from sklearn.datasets import load_iris

# 然后以字典的形式加载鸢尾花数据集，使用y表示数据集中的标签，使用x表示数据集中的属性数据。
data=load_iris()
y=data.target
x=data.data

# 调用PCA算法进行降维主成分分析
# 指定主成分个数，即降维后数据维度，降维后的数据保存在reduced_x中。
pca=PCA(n_components=2)     
reduced_x=pca.fit_transform(x)

# 将降维后的数据保存在不同的列表中
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]

for i in range(len(reduced_x)):
    if y[i] ==0:
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])

    elif y[i]==1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])

    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
        
# 可视化
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

降维结果

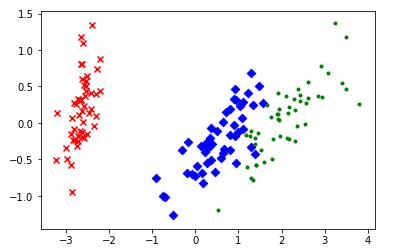
Reference

主成分分析（PCA）原理详解
https://blog.csdn.net/program_developer/article/details/80632779
PCA的数学原理
http://blog.codinglabs.org/articles/pca-tutorial.html
鸢尾花(iris)数据集分析
https://www.jianshu.com/p/52b86c774b0b