ECCV | 达摩院基于局部平坦性的流形学习框架DLME
Posted AI记忆
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ECCV | 达摩院基于局部平坦性的流形学习框架DLME相关的知识,希望对你有一定的参考价值。
本文简要介绍视觉顶级国际会议ECCV 2022接收的论文 “DLME: Deep Local-flatness Manifold Embedding”。实际应用和项目中,数据样本往往是高维的,对高维数据进行学习时,需要在低维空间表示高维信息。从高维数据寻求低维嵌入的方式被称为流形学习。该文提出了一个新的流形学习框架,即深度局部平坦性矩阵嵌入(DLME)。为了克服流形学习遇到的问题,用数据增强的方式来构建语义流形,并使用流形“局部平坦”假设的平滑度约束来克服“结构扭曲”的问题。此外,还设计了一个新的损失函数来克服“约束不足”的问题,并从理论上证明了它是一个局部更平坦的嵌入。同时实验证明了该方法的有效性。
一、论文
论文链接:DLME: Deep Local-flatness Manifold Embedding:https://arxiv.org/abs/2207.03160
二、背景
流形学习 (ML) 旨在从高维数据中寻求低维嵌入。这个问题在现实世界的数据集上具有挑战性,尤其是对于欠采样数据来说,以前的方法在这种情况下表现不佳。流形学习方法将输入数据转换到低维嵌入空间,同时维护数据的几何结构,并随后在低维空间中执行下游任务。欠采样数据的局部连通性差,会导致两个问题:结构扭曲和约束不足的嵌入。本文提出了一个名为 Deep 的新型 ML 框架Local-flatnessManifold Embedding (DLME) 来解决这些问题。
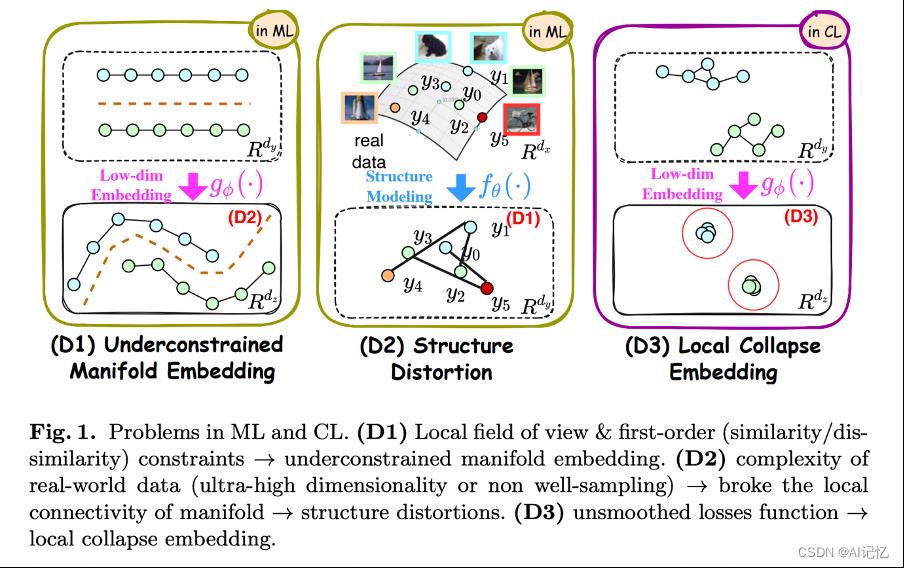
三、方法
)DLME Framework
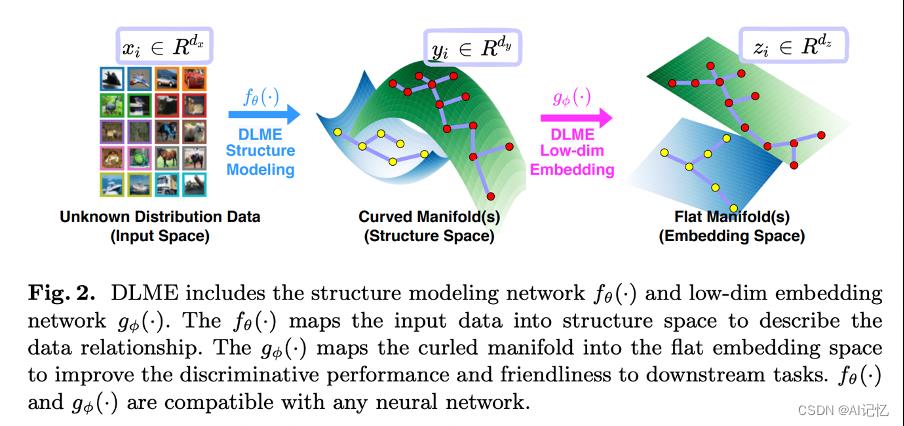
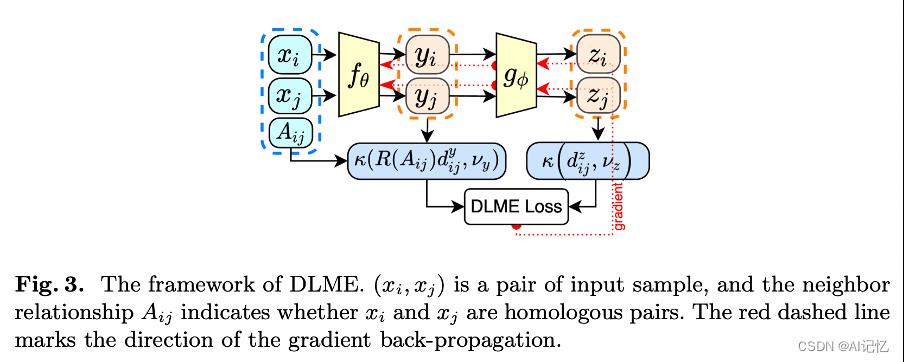
如图2和图3所示,DLME包含了两个神经网络 和
和 以及一个DLME损失函数
以及一个DLME损失函数 。网络
。网络 完成结构建模,网络
完成结构建模,网络 学习低维嵌入,DLME损失函数由
学习低维嵌入,DLME损失函数由 和
和 及
及 空间的pairwise的相似度计算得到。
空间的pairwise的相似度计算得到。 代表了数据对之间的关系,如果
代表了数据对之间的关系,如果 和
和 是同一原始数据通过数据增强得到的话,那么
是同一原始数据通过数据增强得到的话,那么 否则
否则 。
。
a.)用数据增强的方法处理结构扭曲
流形学习方法在处理复杂且欠采样的数据时,很难有效地识别相邻节点,导致结构失真。 DLME用数据增强提供的先验知识解决这个问题。从流形学习的角度来看,数据增强是一种在固有流形中,基于先验知识进行新的观察的技术。由于数据增强尽可能少地改变了原始数据的语义,当流形学习数据的局部连通性被破坏时,它为每个孤立的数据生成了特定的邻域数据。 DLME训练神经网络 。由数据增强和损失函数来指导
。由数据增强和损失函数来指导 将数据映射到潜在空间来较好的保证局部连通性。
将数据映射到潜在空间来较好的保证局部连通性。
前向传播过程为:
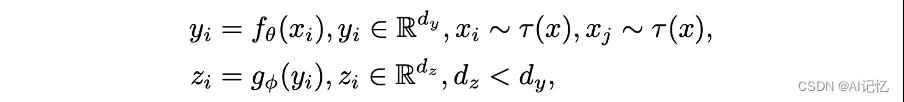
式中, 和
和 是来自同一个原始数据的不同数据增强方式得到的数据,
是来自同一个原始数据的不同数据增强方式得到的数据, 和
和 分别是
分别是 及
及 空间的维度。
空间的维度。
b.)DLME损失函数
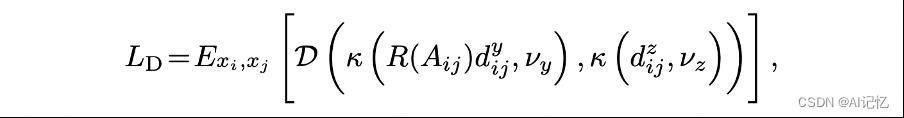
式中 ,
, ,
, ,
,  分别是两个不同空间内点i和点j的距离度量值。用two-waydivergence来度量两个空间的不相似性,
分别是两个不同空间内点i和点j的距离度量值。用two-waydivergence来度量两个空间的不相似性,
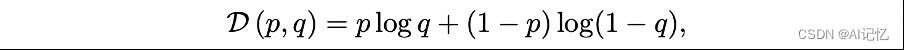
式中 。值得注意的是,
。值得注意的是, 是交叉熵损失函数的连续版本。
是交叉熵损失函数的连续版本。
考虑到结构建模空间需要较大的维度来表达数据之间的关系,而嵌入空间对维度进行了压缩。我们用t分布核函数来计算数据对之间的相似度。
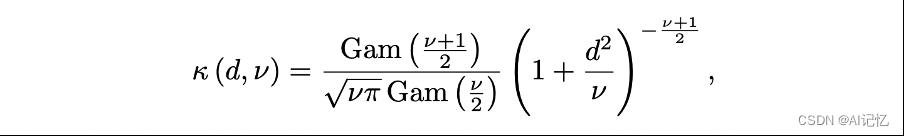
式中,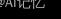 是Gamma函数,自由度v控制核函数的形状。DLME设计
是Gamma函数,自由度v控制核函数的形状。DLME设计 来整合
来整合 中的相邻关系。
中的相邻关系。
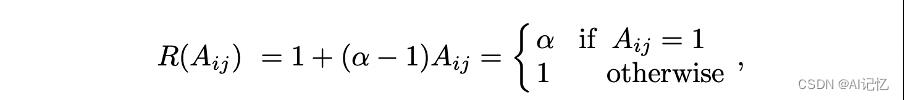
式中,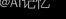 是一个超参数。如果
是一个超参数。如果 和
和 是相邻关系,结构建模空间中的距离会被
是相邻关系,结构建模空间中的距离会被 降低,
降低, 和
和 的相似度会增加。
的相似度会增加。
2.)用平滑对比学习框架处理局部坍缩的问题
自监督对比学习中所用的CL Loss为
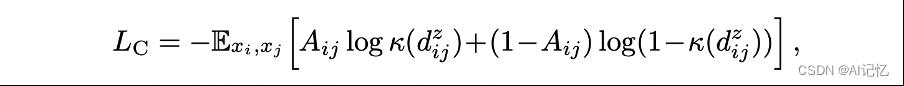
相似度核函数 采用上文介绍的定义。该CL Loss是不平滑的,因为随着
采用上文介绍的定义。该CL Loss是不平滑的,因为随着 的改变,学习目标将会在
的改变,学习目标将会在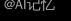 和
和 之间切换。我们提出的DLME Loss是一个更平滑的Loss,CL Loss和DLMELoss的差为
之间切换。我们提出的DLME Loss是一个更平滑的Loss,CL Loss和DLMELoss的差为
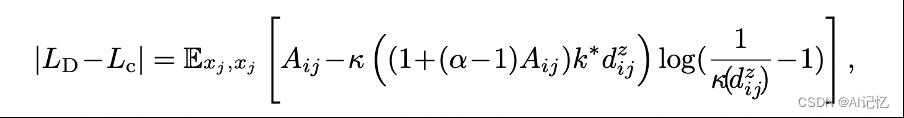
当 ,两个损失函数有一样的作用。当
,两个损失函数有一样的作用。当 ,DLME Loss不会像CL Loss那样去最大化相邻点的相似度,而是根据当前的嵌入结构进行优化。更多的证明过程详见论文和论文附录部分。
,DLME Loss不会像CL Loss那样去最大化相邻点的相似度,而是根据当前的嵌入结构进行优化。更多的证明过程详见论文和论文附录部分。
3.)算法伪代码
算法伪代码参考如下Algorithm1所示。

更多理论证明和详细的分析请参见论文。
四、结果
我们在多个数据集上进行了数据可视化效果的验证,如下图和表1所示,对于复杂的数据来说,流形学习方法(UMAP)不能保证局部的连通性,从而导致了嵌入的失败。我们提出的DLME方法可以得到更好的嵌入结果。
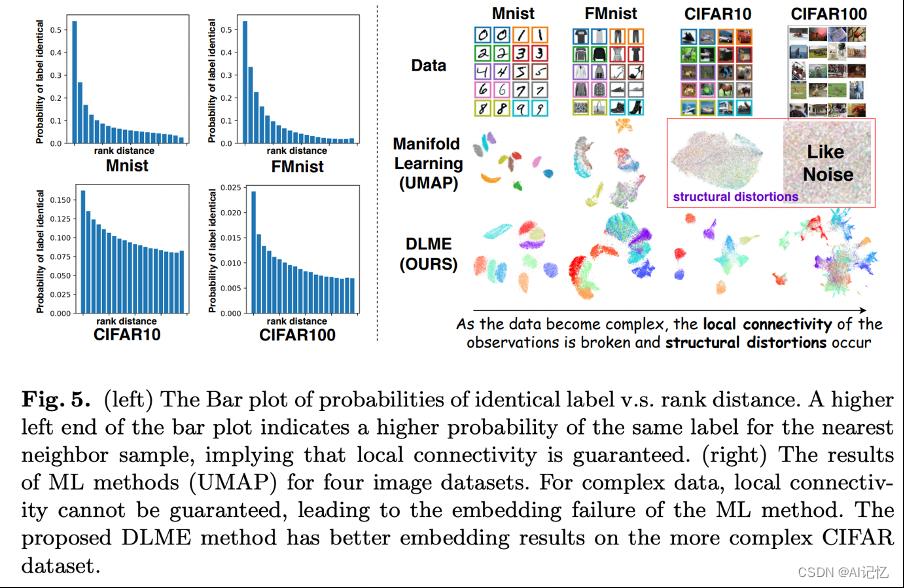
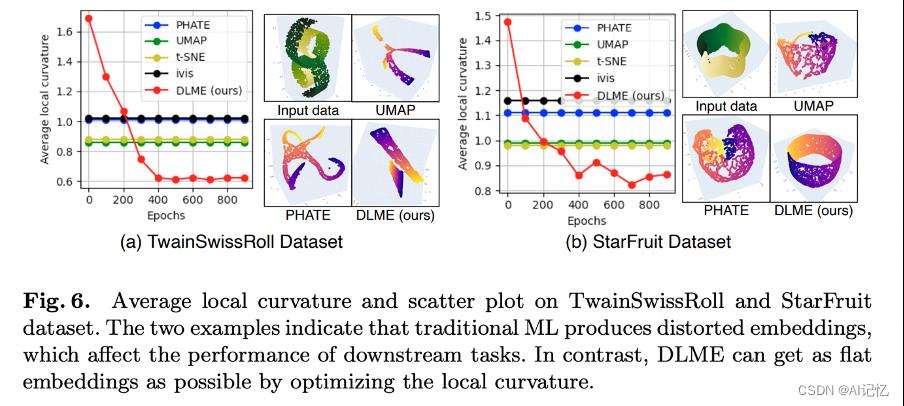
另外在TwainSwissRoll和StarFruit数据集以及生物学数据集上对比了传统流形学习方法和我们的方法。如下列图所示,可以看到DLME都取得了更好的效果。
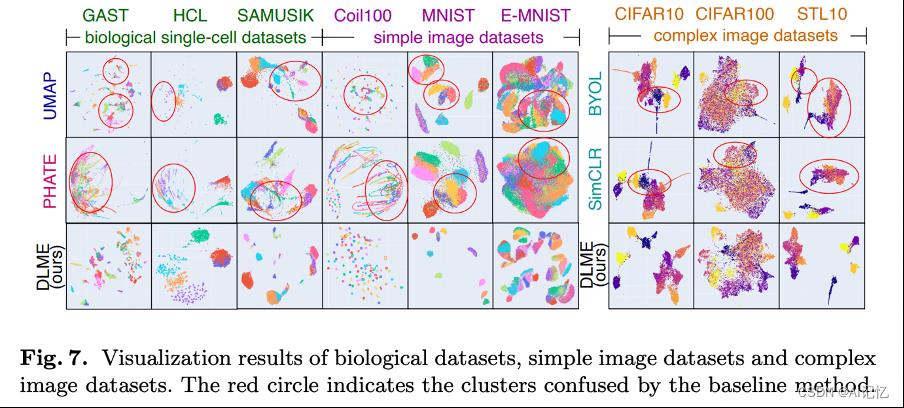
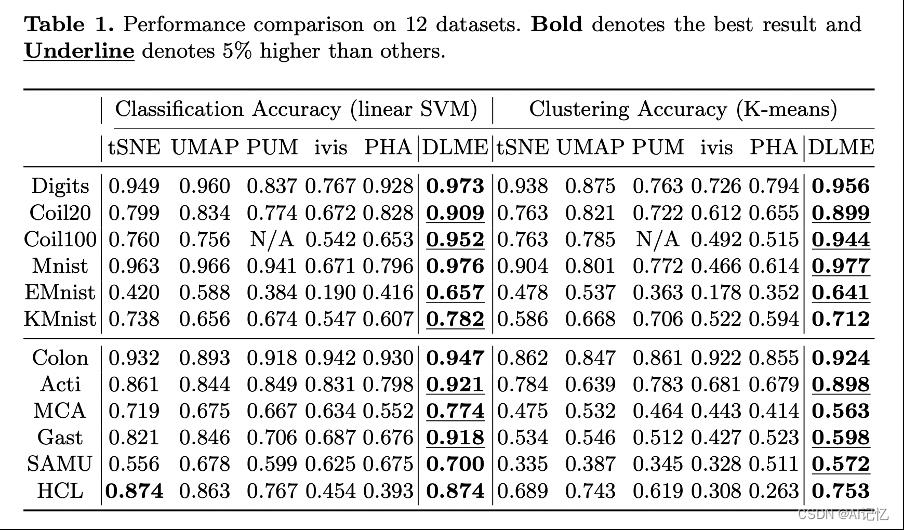
此外进行了对比学习和聚类性能的对比,可以看到,因为平滑对比学习避免了局部的坍缩,DLME方法在这些任务上也都可以取得好的效果。
五、应用
另外给大家介绍下CV域上的开源免费模型,欢迎大家体验、下载(大部分手机端即可体验):
https://modelscope.cn/models/damo/cv_resnet50_face-detection_retinaface/summary
https://modelscope.cn/models/damo/cv_resnet101_face-detection_cvpr22papermogface/summary
https://modelscope.cn/models/damo/cv_manual_face-detection_tinymog/summary
https://modelscope.cn/models/damo/cv_manual_face-detection_ulfd/summary
https://modelscope.cn/models/damo/cv_manual_face-detection_mtcnn/summary
https://modelscope.cn/models/damo/cv_resnet_face-recognition_facemask/summary
https://modelscope.cn/models/damo/cv_ir50_face-recognition_arcface/summary
https://modelscope.cn/models/damo/cv_manual_face-liveness_flir/summary
https://modelscope.cn/models/damo/cv_manual_face-liveness_flrgb/summary
https://modelscope.cn/models/damo/cv_manual_facial-landmark-confidence_flcm/summary
https://modelscope.cn/models/damo/cv_vgg19_facial-expression-recognition_fer/summary
https://modelscope.cn/models/damo/cv_resnet34_face-attribute-recognition_fairface/summary
以上是关于ECCV | 达摩院基于局部平坦性的流形学习框架DLME的主要内容,如果未能解决你的问题,请参考以下文章