Java基础笔记 进制与进制转换
Posted 糖醋酸辣椒
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java基础笔记 进制与进制转换相关的知识,希望对你有一定的参考价值。
---恢复内容开始---
进制
在一般生活中,我们一直在应用的十进制,就是逢十进一,而今天我们要接触的是,计算机编程常用的进制!首先我们要知道,计算机内部运算采用的是二进制,也就是逢二进制!
1.什么是二进制?
就是只有0 和 1 每当遇到值为2 就向前进一位。
2.为什么计算机内部是二进制?
这就要从硬件说起,计算机是如何储存数据的,要知道我们网络传输,就是你要和别人一起聊天,你们隔着很远,到底是怎样才能让他收到你的聊天内容? 有一根网线还能说过去,毕竟网线链接终端我们也不知道连到哪,保不齐就是全世界都是用网线链接。但是无线的时候为什么还是可以聊天内容又是怎么算的?
附:我们网路传输主要是更具我们电脑从应用层到物理层硬件设备,物理层将数据链路层数据帧转换为传输介质相应的信号形式,如光信号、电磁波信号等然后由路由器通讯,只要不是同一个网络,我们传输都要依靠路由。在这样说就扯远了,简单地说,我们计算机为什么要用二进制,到底和上面的有什么关系?正是因为我们用的的是电和光传播数据,那么在硬件设备要识别这些电和光传输的是什么是很麻烦的,比如给他弄个什么形状是代表什么,这太复杂而且传输太不稳定一开始就被淘汰这种想法,到后来那些大神们就规定 波长呈升型表示1 波长呈降型就表示0 平行表示不变,因为就只有这两种形态,所以使用二进制最合适,所以计算机内部是二进制!
注意:在我们JAVA教程一般讲的是我们计算机传输电信号开就是1 关就是0这是一种形象的说法。毕竟我们了解二进制而他具体是怎么实现计数的没多大必须性。
那么就来简单模拟一下JAVA教程最常让我们理解的一种方式
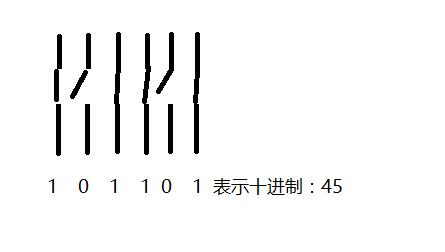
看图片 ,通电状态标识1 不同电表示0.
综上所述,你只要简单明白:这是由计算机的工作原理决定的,计算机进行运算实际是靠的电路,电路的逻辑只有0和1两个状态,这里的0和1并不是数字的0和1,0和1是表示两种不同的状态,0表示低电平,1表示高电平。因为计算机是由无数个逻辑电路组成的,只能根据0和1的无限位数和组合来表达信息。所以二进制是最接近计算机工作模式的,也是计算机直接能读懂的,其他高级语言都需要转义成机器语言。
我们要学习的不是计算机怎么去采集电信号和光信号,而是知道计算机常用的进制:1.十进制 2.二进制 3.八进制 4十六进制
1.十进制逢十进一位 也就是 1 2 3 4 5 6 7 8 9 到了十 怎么表示的 就是10 他就进了以为
2.二进制逢二进一位 也就是 0 1 到了2的时候 他也仅为 10 在二进制这个表示2不是10哦
3.八进制逢八进一位 也就是 0 1 2 3 4 5 6 7 到了8的时候,他就进一位 10 表示 十进制的8
4.十六进制逢十六进制 也就是 0 1 2 3 4 5 6 7 8 9 A(10) B(11) C(12) D(13) E(14) F(15) 6不6 数字不够,字母凑。
知道这些进制有什么用,不知道你有没有这个疑问?为什么要学习它?
目前在我们后面要学会数据类型和位运算都是需要进制的知识,具体是进制哪方面的知识呢?就是即将要讲的 进制转换!
进制转换:就是这些进制之间的互相转化,计算机内部计算是二进制,那么到底我们打开系统的计算机,他是什么原理,让我们可以进行十进制运算?是怎么做到的,这个是今天的主要针对内容!
看不懂八进制和十六进制没关系,先尝试去理解意思,其他具体数字转换得值可以忽略,等看了十进制转二进制再回头来看一遍!
首先我们要知道的是八进制:
八进制的特点是逢八进一位。那么来看下面这一段二进制数:0111 打开计算机,选择程序员类型。(不会选自己百度)
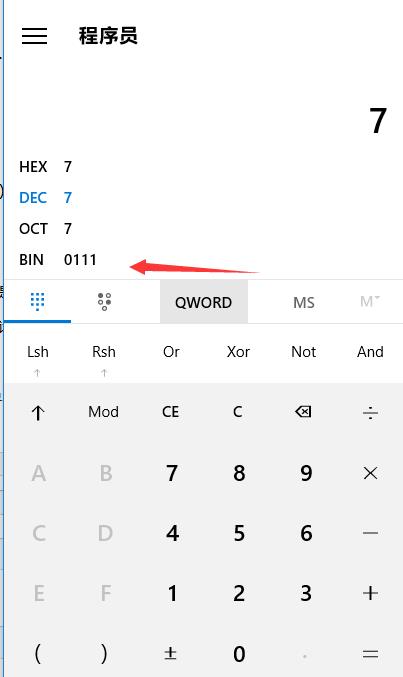
BIN:二进制 HEX:十六进制 OCT:八进制 DEC:十进制!
没错这个数字表示7。
在哪我们在看一个二进制数:1000
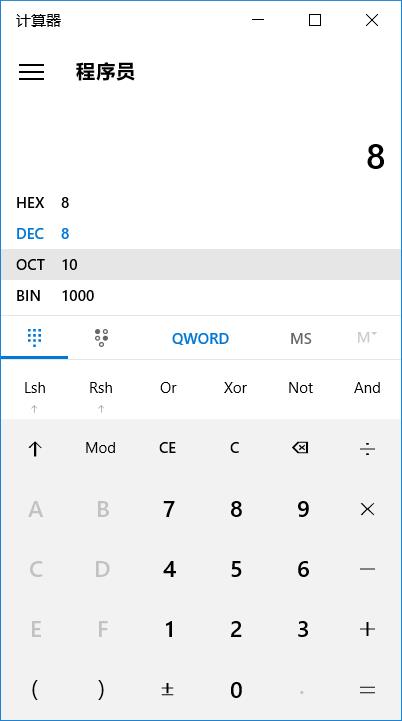
注意看:OCT写的是不是 10 是不是向前进了一位?
所以八进制我们用二进制一般这样去转换 三个二进制位表示八进制的一位!
十六进制同理,我就不用计算机了,直接给你写出来
二进制转十六进制:
因为二进制1111 表是的就是15 而十六进制是16进一,所以二进制转十六进制是 四个二进制位表示十六进制一位。
那么明白了这点,我们来做几个练习题:
00010001 计算出他的十六进制和八进制
二进制: 000010001
八进制: 000 010 001
最终答案:0 2 1 所以是:21
卧槽,怎么搞的这个数难道是21 我怎么用计算机计算出的21并不是这个答案,于是开始慌了!

这是一个用对进制不熟悉造成的,注意我们求得是二进制对八进制,我们别看DEC这个是十进制。如果你和我一样是WIN10首先要去点击OCT然后在看BIN是多少

没毛病吧! 然后我们通过这个转换还明白了一个点记住:进制不会我们就用计算机转呗,反正又不是常用,算法能记就记,记不住我们就用计算机,实在想找算法就百度呗!
好了八进制是没毛病了,我们再看十六进制例子:
BIN:00010001
HEX:0001 0001
转换:11
明吧了吧,就是把二进制转分割然后分别计算出他们的值,这样能达到快速转换!
十进制转二进制:
看了上面的转换估计有一个疑问 0001你怎么就知道是1 ? 这不乱讲么,我都不知道为什么0001是 1额。别急,学了十进制转二进制,不管多少进制你瞬间就能明白了!
首先学十进制转二进制 我们用最原始的表达式来学习:十进制转二进制就是一直用十进制除以2,出尽后最后是1则最后一位是1 如果出尽最后一位则是0,从下往上排列!注意这个原始算法对于十六进制和八进制都是通用的,最主要的是八进制和十六进制,要分割 比如十六进制 2F 两位数,要知道一位十六进制表示的是 0000 四个个二进制位 所以 分别用来除以2 然后按照位置前后组合得到的0和1 八进制也是同理,八进制是三个位,就这里和十六进制不同,按三个位分!
例:我们现在要将10转换为2进制
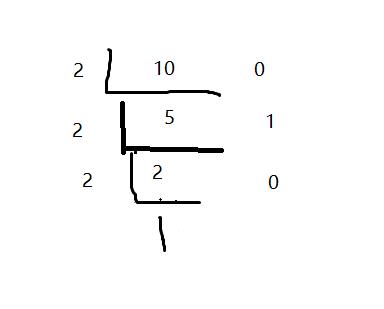
解析:就是一直除以2 在第一次10/2=5 没有余数,所以此位置就是0 然后在得的数5 再除以2 5/2=2%1 所以此位置是1 得到2,此时2/2=1 所以最终答案:1010

此时我们在做两个例子
将十进制25转换成二进制数: 2 | 25 1 ------ 2 | 12 0 ------ 2 | 6 0 ---- 2 | 3 1 ------ 1 从下往上排列就是二进制数:11001
那么学了十进制,那么十进制转二进制怎么算呢?整数二进制用数值乘以2的幂次依次相加,小数二进制用数值乘以2的负幂次然后依次相加!
举个例子: 0101 转 十进制
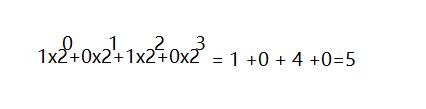
这就是进制转换,如果你是新手,来看我资料,估计我这个资料有点针对我个人写的,那么我给你找几个文章学习进制转换:
http://jingyan.baidu.com/article/495ba84109665338b30ede98.html
http://www.cnblogs.com/syqlp/p/6586995.html
http://blog.csdn.net/xy2204/article/details/50522075
二进制快速转十进制方法:
以8位 来演示:
1.第一种:
00000001 1
00000010 2
00000100 4
00001000 8
00010000 16
00100000 32
01000000 64
10000000 128
2.第二种:
00000001 1
00000011 3
00000111 7
00001111 15
00011111 31
00111111 63
01111111 127
3.第三种:
10000000 128
11000000 192
11100000 224
11110000 240
11111000 248
11111100 252
11111110 254
举个例子: 11101011
可分为:
11100000(上面第三种类型) 224
00001000(上面第一种类型) 8
00000011(上面第二种类型) 3
我们通过记住上面三种类型的转换,再用加 法(加法口算你会吧)立即得到结果:235
==================================================================================
方法二:
熟记以下排列,其实很Easy了,从右往 左,依次是前一个数的2倍:
256 128 64 32 16 8 4 2 1
随便写个数字比如48
48 = 32 + 16,所以在32 和 16所在的位置为1,其余为0,
转为2进制就是
256 128 64 32 16 8 4 2 1
0 0 0 1 1 0 0 0 0
二进制转十进制就更简单了,
比如随便写的一串 01111101
先写上 : 0 1 1 1 1 1 0 1
然后填充 128 64 32 16 8 4 2 1
十进制为 64+32+16+8+4+1=125
看不懂只能自己去看视频,这边听边讲的好学会,用文字这个样给你说,你本来没点基础,我是没法让你看懂的!
---恢复内容结束---
以上是关于Java基础笔记 进制与进制转换的主要内容,如果未能解决你的问题,请参考以下文章