数字信号处理相关1（卷积(convolution)的几种解释）

Posted 2022-12-14 Times_poem

来自：https://blog.csdn.net/bitcarmanlee/article/details/54729807

来自：https://www.zhihu.com/question/22298352

 

啰嗦开场白
读本科期间，信号与系统里面经常讲到卷积(convolution)，自动控制原理里面也会经常有提到卷积。硕士期间又学了线性系统理论与数字信号处理，里面也是各种大把大把卷积的概念。至于最近大火的深度学习，更有专门的卷积神经网络(Convolutional Neural Network, CNN)，在图像领域取得了非常好的实际效果，已经把传统的图像处理的方法快干趴下了。

 

概念说明：

 

卷积本身就是一个非常抽象的数学概念，抽象到很难拿现实生活中通俗易懂的例子去解释。去理解那些复杂的例子，有时也很烧脑甚至会越看越懵，还不如直接看公式来的直观。

 

概念

卷积（convolution）是一种数学运算，废话不多说，先看公式。

 

对于序列x(n)和h(n), 卷积的结果是：

 

对于函数x(t)和h(t), 卷积的结果是：

 

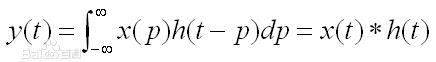
卷积的本质是两个序列/函数的平移，加权叠加。

 

 

应用举例

卷积在现实生活中，很难找到一个比较通俗易懂的例子，就以一个它在信号与系统中典型的应用为例吧，我也看过网上很多人举的例子，还是感觉这个更直观一点。

 

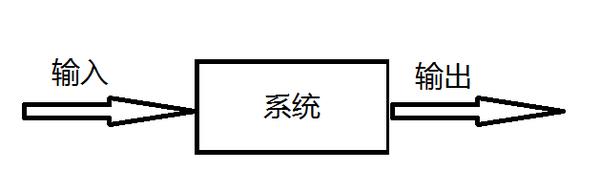
通俗易懂的说，就是

输出 = 输入 * 系统

 

所以为什么卷积这么重要，懂了吧？虽然它看起来只是个复杂的数学公式，但是却有着重要的物理意义，因为自然界这样的系统无处不在，计算一个系统的输出最好的方法就是运用卷积。

 

 

其他应用

统计学中，加权的滑动平均是一种卷积。

概率论中，两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。

声学中，回声可以用源声与一个反映各种反射效应的函数的卷积表示。

电子工程与信号处理中，任一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得。

物理学中，任何一个线性系统（符合叠加原理）都存在卷积。

计算机科学中，卷积神经网络（CNN）是深度学习算法中的一种，近年来被广泛用到模式识别、图像处理等领域中。

 

 

第一种解释： 知乎上排名最高的解释
首先选取知乎上对卷积物理意义解答排名最靠前的回答。 

 

不推荐用“反转/翻转/反褶/对称”等解释卷积。好好的信号为什么要翻转？导致学生难以理解卷积的物理意义。
这个其实非常简单的概念，国内的大多数教材却没有讲透。

直接看图，不信看不懂。以离散信号为例，连续信号同理。

已知

 

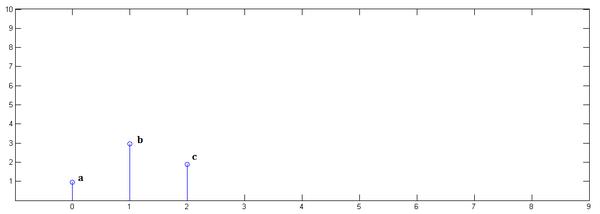
已知

 

下面通过演示求的过程，揭示卷积的物理意义。

第一步，乘以并平移到位置0：

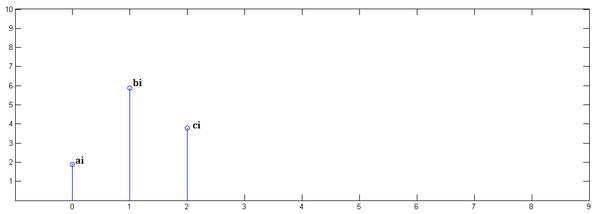
第二步，乘以并平移到位置1：

第三步，乘以并平移到位置2：

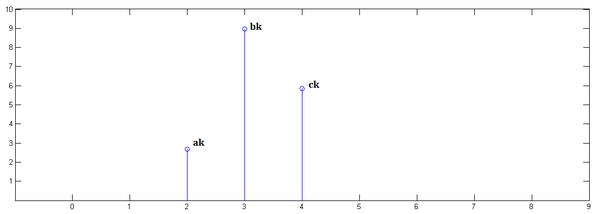
最后，把上面三个图叠加，就得到了：

简单吧？无非是平移（没有反褶！）、叠加。

 

====================================================

从这里，可以看到卷积的重要的物理意义是：一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。

 

重复一遍，这就是卷积的意义：加权叠加。

对于线性时不变系统，如果知道该系统的单位响应，那么将单位响应和输入信号求卷积，就相当于把输入信号的各个时间点的单位响应 加权叠加，就直接得到了输出信号。

 

通俗的说：
在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。
这正是单位响应是如此重要的原因。

 

 

第二种解释 《卷积信号与moba游戏的伤害计算》

在打游戏的时候，假设你对敌方英雄造成了一次攻击。攻击的效果是，地方英雄会在接下来5秒内持续增长的掉血。每秒掉血分别为1 2 3 4 5；那么你在0秒的时候攻击了一下敌方英雄，敌方英雄的掉血情况为：

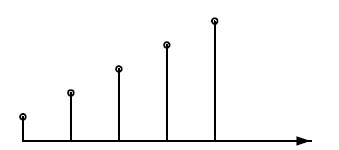
抽象一下。假设x[k]是一个单位信号（一次攻击），即仅当k=0时x(k) = 1.假设把这个信号输入到一个系统里面得到的响应为h[n]：

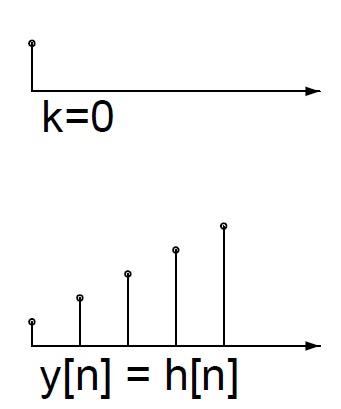
同样，假设你在第2秒对地方英雄进行了攻击，则敌方英雄会在地2-7秒持续掉血。

由于攻击不是在第0秒，而是在第二秒，因此，产生伤害也是从第二秒开始。使用函数位移的想法了解释，则本来第0秒产生的伤害右移了两个单位，变成了h[n-2]：

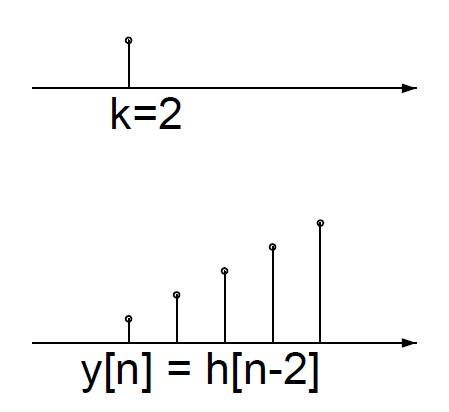
那么，如果第0秒和第2秒都进行了攻击，伤害是怎样的呢？当然是第0秒的伤害加上第2秒的伤害，即：

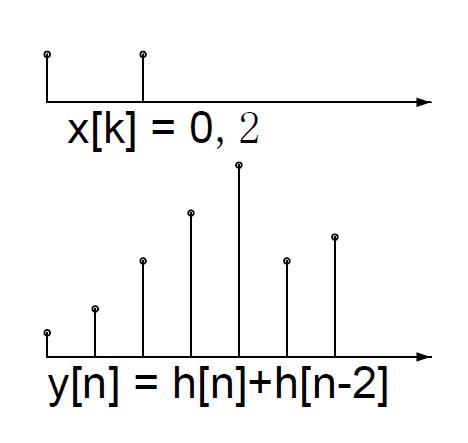
那么，对于任意形式的攻击x[k]，很容易推广到，产生的伤害y[n]计算方法为：

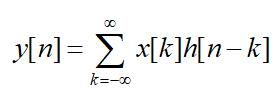
这就是卷积的公式。解释很简单，就是对任意的攻击x[k]，产生的伤害就是，把所有k时刻的攻击产生的伤害h[n-k]都叠加起来了。

那么，如果我想知道，对与任意的攻击方式，敌方英雄某一秒（比如第3秒）受到的伤害是怎样的呢？

即，对于输入x[k]，任意一个y[n]点的伤害是怎样的呢？

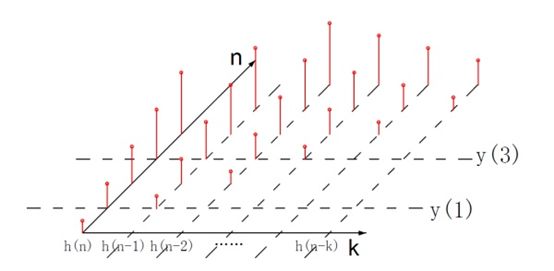
我把不同k时候的关于n的函数h[n-k]全部画出来。如上图中不同的纵轴表示。那第三秒敌方英雄收到的伤害y[3]等于x(0) h(3)+ x(1) h(3-1)+ x(2) h(3-2)+ x(3) h(3-3).

注意！！！在上图的表示中，我并未直接计算 ，而是将其表示为不同的函数h[n-k]与不同的[k]的组合！！

 

------------学术的分割线--------------

 

也就是说，以离散信号为例，

卷积y[n] = x[n] * h[n]，可以理解为，将y[n]分为不同的 分量为h[n-k]、系数为x[k]的线性组合。也就是说，y[n]是一系列关于h[n]移位后的h[n-k]，每个函数h[n-k]乘上特定的系数x[k] 组合而成的函数。

这种 “用一组函数进行线性组合得到目标函数”的理念，在傅里叶分析中也有应用：将原始信号y[n],分为一系列谐波信号e^（jkwn）的函数的线性组合。

再来看这个图：

你想到了什么？？

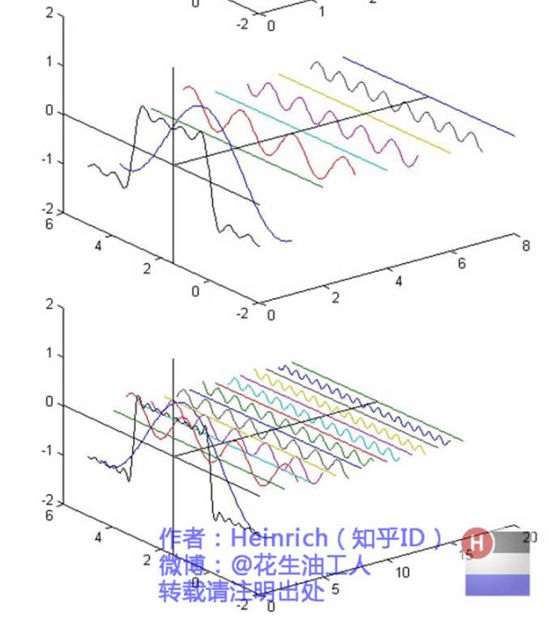
上图解释参见：如果看了这篇文章你还不懂傅里叶变换，那就过来掐死我吧

到这里会发现，卷积和傅里叶分析的一个相同的理念：

用不同的函数的线性组合，表示原信号。

傅里叶分析用的是不同的正弦函数的线性组合；

而卷积，用的是h[n]移位不同的k得到的一系列h[n-k]的线性组合。

换个角度，你会看到更多。

 

 

第三种解释 卷积及卷积神经网络

 

“卷积”这个词在很多领域都有出现和应用，比如统计学、声学、物理学、计算机科学等等，相信很多人第一次听到它时都是一脸懵逼的状态。在深度学习领域中，卷积是一个很常见的术语，我们常用的卷积神经网络就用到了卷积，而卷积也是卷积神经网络拥有良好的图像处理能力的关键。但可能很多人并没有很好地理解卷积，很长时间都处于似懂非懂的状况，今天我们就直观解释一下深度学习中的卷积。

 

什么是卷积？

你可以将卷积想象成一种混合信息的方法。想象有两个装满信息的桶，我们把它们都放到一个桶里，然后根据某种规则搅拌搅拌。每个信息桶都有它自己的配方，写明了桶里的信息该如何同另一个桶的信息混合在一起。所以卷积就是两个信息源混合在一起的有序过程。

我们也可以从数学上描述卷积，实际上卷积就是一种数学运算，和加减乘除差不多。虽然这种运算本身比较复杂，但非常有助于简化更为复杂的方程式。在物理和工程学中，卷积同样被广泛用于简化复杂的公式。

 

怎样将卷积应用到图像处理中？

我们在图像处理中应用卷积时，是将其应用在二维数据中——即图像的宽和高。还是用前面举的混合两个桶的比喻，第一个桶是输入图像，总共 3 个像素矩阵——每个矩阵对应红、绿、蓝 3 个颜色通道；每个通道中的每个像素都是 0-255 之间的一个整数。第二个桶是卷积核（kernel），它是一个浮点值矩阵，其中的数字模式和大小就相当于桶的配方，写明了应该怎样将输入图像和卷积核搅拌在一起，在卷积操作中就是将卷积核与输入图像混合在一起。卷积核的输出是一幅修改后的图像，在深度学习中常被叫做特征图谱（feature map）。每个颜色通道都会有一个特征图谱。

 

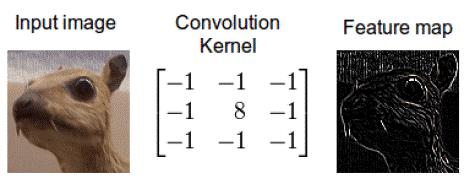
将图像和边缘检测器的卷积核混合的卷积操作

 

上图如何做到呢？我们现在就演示一下通过卷积将这两部分信息搅拌在一起。应用卷积的一种方法就是从输入图像中取出一个和卷积核大小相同的区块——这里我们的图像为 100 x 100，卷积核为 3 x 3，所以我们取得区块为 3 x 3——然后对图像区块和卷积核的每对相同位置的元素执行乘法后求和（即 element-wise 乘法，是两个相同大小的矩阵的“点乘”）。

 

乘积的和会产生特征图谱中的一个像素。待特征图谱中的一个像素计算完毕后，图像区块提取器的中心会移动一个像素，对下个区块执行相同的操作，重复这个计算。直到按照这种方式计算出特征图谱中所有像素后计算才会停止。这个流程可以用如下的 GIF 演示：

 

上图为获得特征图谱中一个像素的卷积操作：RAM 表示输入图像，红色区域表示选取的图像区块，然后将其和卷积核相乘，得到的乘积和变为特征图谱（Buffer RAM）中的一个像素。

你可能注意到这里还有个正则化过程，以卷积核大小 9 作为正则化因子 m 将输出值进行正则化处理，这是为了保证图谱的整体亮度和特征图谱保持一致。

 

为何图像的卷积在机器学习中如此有用？

在机器学习图像处理中，图像可能含有很多对我们无用的噪声数据。比如有个机器学习项目，基于深度编码器的搜索引擎：上传一幅时尚服饰的图片，编码器自动找出款式类似的服饰。

集智此前也分享过一个类似项目：

景略集智：技术宅如何进化为女装大佬​zhuanlan.zhihu.com

 

如果你只想区分衣服的样式，那么衣服的颜色就没那么重要了，像商标之类的细节更不重要。最重要的是衣服的外形。一般而言，女式衬衫的形状与衬衣、夹克和裤子的外观很不一样。假如我们的模型能过滤掉这些无用的噪声数据，那么模型就不会受到颜色、商标相关的数据信息的影响。而我们通过卷积就能轻松实现这种操作。

 

项目作者对数据进行了预处理，应用了一个 Sobel 边缘检测器（和上面的卷积核相似）来过滤图像中除了边缘外的所有信息——这也是为何卷积应用常被称作滤波（filtering）、卷积核常被称为滤波器（filter）的原因。边缘检测器生成的特征图谱对区分衣服类型作用很大，因为只有相关的外形信息被保留下来。

 

 

模型的输入和输出：左上图为搜索请求，其它图像为模型的输出结果。你可以看到模型真的只关注了衣服外形，而非颜色。

我们可以再深入一步：模型中有很多不同的卷积核，能够生成很多不同的特征图谱，比如锐化图像（细节更多），或模糊图像（细节更少），每个特征图谱都能帮算法更好的完成任务。

 

这里所用的“选取输入——转换输入——将转换后的输入喂给算法”就被叫做特征工程。特征工程非常困难，很少有人能熟练地在多个领域应用特征工程。它之所以很难是因为每种数据每种问题中，它的有用特征是不同的，非常依赖个人经验。

所以特征工程对新手来讲特别困难。不过对图像而言，是否能够做到用卷积核自动找出某个任务中最适合的特征？

估计你也猜到了，我们用的卷积神经网络就是干这个的。和前面使用固定大小的卷积核不同，我们会给卷积神经网络中的卷积核赋予参数，参数会在数据上得到训练。随着卷积神经网络的训练，卷积核为了得到有用信息，在图像或特征图谱上的滤波工作会越来越好。这个过程都是自动完成，我们只需在新数据上训练自动找出新的滤波器就行了，这也是为何卷积神经网络在图像处理中如此强大的原因。

 

 

一点补充

 

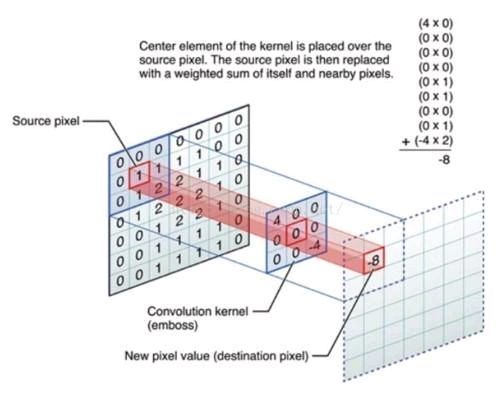
----出自《深度学习原理与TensorFlow实践》一书

 

第四种解释 卷积->滤波器   （频域相乘等于时域卷积）

 

很古老的问题了，前面高赞答案大多还是从时域的“加权求和”角度理解，我来给大家换个思路。

以下三张图片均为，左侧时域，右侧频域

采样频率 Fs = 1000 
采样点数 N = 200

 

第一张图是

 

即四种不同频率的信号叠加，从右侧频谱图中可以清晰看出

第二张图是低通滤波器 ，为啥说他是低通滤波器呢，你看它频域只有低频部分，如果这个低通滤波器和其他函数频域相乘，结果会加强 1~100 的低频部分，削弱 100~500 的高频部分。

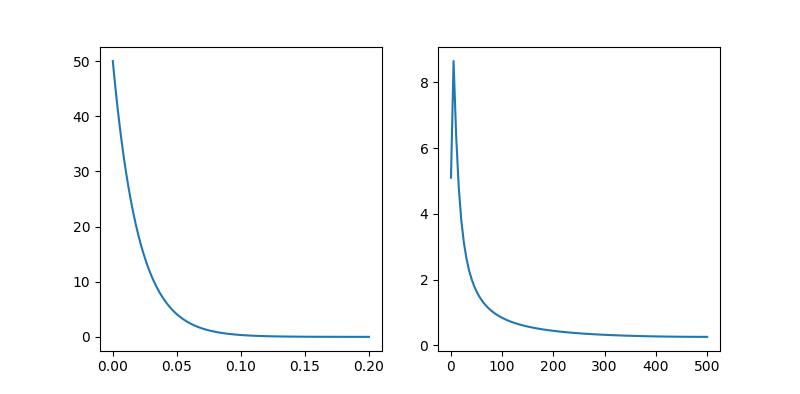
第三张图是前两个卷积后的结果，一组信号与低通滤波器卷积，实质是提取出信号中的低频分量，一目了然

PS: 经过处理的信号仍然留有一点点高频分量，如果用性能更好的滤波器函数，会得到更好的效果，而本文中为了方便大家理解，只使用这个工科生都见过的一阶 RC 低通电路作为示范

 

 

第五种解释 

最近在看Feedback Control of Dynamic Systems，趁此机会复习了一下卷积。

先看下图，左边是输入信号，右边是输出信号：

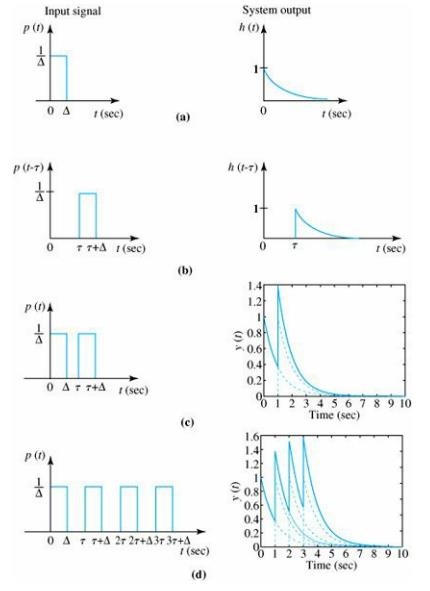
(a)中，输入信号p(t)经过系统后得到输出信号h(t)；
(b)中，输入信号较之于(a)延迟了τ，表示为p(t-τ)，由于是LTI（线性时不变系统），输出信号也延迟τ，变为h(t-τ)；
(c)、(d)两图阐释了LTI的叠加原理：若以p(t)+p(t-τ)为输入，则输出为h(t)+h(t-τ)；

 

假设现在有一个输入信号u(t)，将其表示为若干个我们刚刚见过的p(t)的叠加

 

 

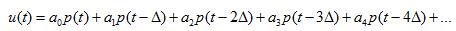
那么u(t)通过上文的系统后，会得到什么呢？
假设可得y(t)，根据叠加原理：

 

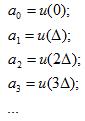
但我们仍有一些不太满意的地方，用p(t)表示的u(t)并不是精确的u(t)啊，那些小长条的面积比u(t)的面积可少了不少呢。除非Δ尽可能的小，长条尽可能的窄。

 

诶，这不就是积分么？

所以：

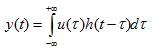
这就是卷积，与其理解成翻转，不如理解成延迟后叠加。