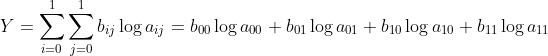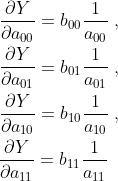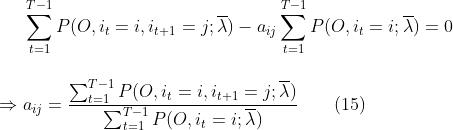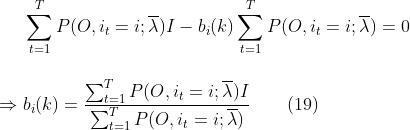大道至简机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解---学习问题：Baum-Welch算法推导
Posted 尚拙谨言
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了大道至简机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解---学习问题：Baum-Welch算法推导相关的知识，希望对你有一定的参考价值。
☕️ 本文往期系列文章：【大道至简】机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解（1）---开篇：基本概念和几个要素_尚拙谨言的博客-CSDN博客
【大道至简】机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解（2）---计算问题：前向算法和后向算法_尚拙谨言的博客-CSDN博客
☕️ 本文来自专栏：https://blog.csdn.net/qq_36583400/category_11959999.html
❤️欢迎各位小伙伴们关注我的大道至简之机器学习系列专栏，一起学习各大机器学习算法
❤️还有更多精彩文章（NLP、热词挖掘、经验分享、技术实战等），持续更新中……欢迎关注我，个人主页：https://blog.csdn.net/qq_36583400，记得点赞+收藏哦！
📢个人GitHub地址：https://github.com/fujingnan
目录
写在前面
阳康后，赶紧捡起续篇，本篇是继上篇 概率计算问题后，介绍的又一个重要的HMM经典问题---学习问题。学习问题主要算法就是Baum-Welch算法，在学习推导这个算法的过程中，简直要了我的命。特别是对于状态转移概率矩阵的参数估计，先后咨询了七月在线的学员、前同事（一个牛逼的数学专业的留美硕士），各大QQ群和微信群，百度搜索结果几乎遍历了个遍，甚至拉上我对象一块思考（她数学脑子比我好使）……总之，真的体会到了想要学好一个东西，就要绞尽脑汁千方百计不择手段……最终一定能成功！
在我搞懂算法推导后，我体会最深的就是学习一个算法，课本并非是唯一的选择，原因很简单，好几页的公式推导浓缩成几行，你看不懂很正常。网上搜出来的博客也并非是好的选择，那种和课本如出一辙的套路，能把你讲明白才怪。作者本身懂不懂我不清楚，反正肯定没法给读者讲懂。
所以总结一下我是怎么学习的：课本+所有可调动的资源（包括自己的脑子）。这篇文章，我要尽全力写成网上最好的Baum-welch详解博客，我会把我掌握的知识一步一步推给大家，让大家应懂尽懂。
一、何为学习问题
在概率计算问题中，我们都是已知了模型参数λ和观测结果，然后计算在已知模型λ的条件下，出现观测O的概率，因为该有的已知条件都有了，所以问题就简单了。但是，如果我们并不知道模型参数λ是啥，只观测到了结果是啥，这个时候如果我们想得到导致该结果出现的模型参数λ，该咋办？看上去有点无中生有了。那么对于这种无中生有的问题，只能靠已知的观测结果以及已有的数据来学习得到模型参数了，这就是学习问题需要做的事，这一点和深度学习中的模型训练思想特别类似。只不过这里我们用到的是无监督的学习方法，不需要人工进行样本的标注，隐马尔科夫模型中的学习方法用的就是Baum-welch算法，所以，本篇我们就来详细介绍一下Baum-welch算法的原理。
二、Baum-welch算法的概念
因为我们现在只有观测数据，而要仅通过观测数据来推导隐马尔科夫模型参数λ，怎么做呢？通过前几篇文章的介绍我们知道，每个观测值的背后都隐藏着一个隐状态，也就是说，一组观测值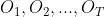
对应着一组状态序列
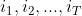，换句话说，学习问题中的隐马尔科夫模型其实就是一个含有隐变量I的隐马尔科夫模型。求解含有隐变量的模型，其实就是求解含有隐变量的模型参数估计问题。学过EM算法的同学一定对这句话特别熟，没错，Baum-welch算法本质上就是EM算法，EM算法就是要解决这种含有隐变量的参数估计问题。所以要学懂Baum-welch算法，还是需要先学好EM算法的基础，大家可以参考我写过关于EM算法原理介绍的博客。当然，Baum-welch算法提出的时候，还没有提出EM算法，但是很多教科书基本上都是把EM的学习放在前，Baum-welch算法放在后，因为EM更加通用更加基础。
总的来说：Baum-welch有如下描述
假设给定训练数据只包含S个长度为T的观测序列
而没有对应的状态序列，比如上一篇的例子中，我们只观测到红球，白球，红球，目标是学习隐马尔可夫模型λ=(π，A，B)的参数π、A、B。如果将观测序列数据看做观测数据O，状态序列数据看做不可观测的隐数据I，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型
为了等会推导方便，这里公式编号我直接和《统计学习方法》中的编号对应上。顺便插一嘴，公式里我用的分号，分号后的参数代表该参数参与公式计算，而|后的参数表示在该参数已知的条件下。书中不用分号，用的是|，这样容易和条件概率中的|混淆，所以我这边用分号代替。关于该公式为啥这么变换，我在我往期博客中说了很多遍了，就是对一个边缘概率转化成联合概率求和的形式。
三、 重温EM算法
既然Baum-welch算法的本质就是EM算法，那我想还是稍微复习一下EM算法推导吧，大家也可以直接跳到这里详细阅读学习以下EM算法，为了高效复习，这一节EM算法的讲解我会按照《统计学习方法》中EM算法章节的内容做推导，而且比书上更详细易懂。磨刀不误砍柴工，走起~
EM算法的用武之地就是要通过公式10.32来得到概率模型的完全数据的对数似然函数（所谓完全数据，说白了就是可观测和不可观测变量都要体现在概率模型中），并通过极大化该似然函数来估计公式中的各项参数，从而得到模型。所以这里通过公式10.32得到的完全数据的对数似然函数就是
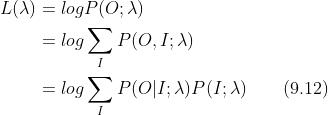
由于EM算法的求解也是采用迭代的思想，因为我们要极大化似然函数，所以迭代的趋势就是每一次迭代得到的似然函数值都比上一次大，也就是说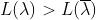
一定要成立。
表示上一次迭代得到的参数值，是个已知量。现在我们来考虑一下两者的差：
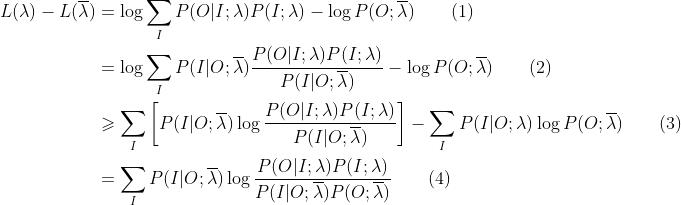
上述公式是EM算法的核心，理解上面的公式非常之重要，现在我们来看一下每一步是怎么得到的：
（1）-（2）：这其实就是用到了一个技巧，分子分母同时乘以一个数，原式不变，这同时乘以了一个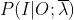
，至于为什么要乘以这个东西，是为了后面要用到的Jessen不等式，至于原创是怎么想到的，这个自己去问他~不过我推测原理大概就是因为，我们的EM算法要解决的是已知观测序列未知状态序列的问题，也就是在观测已知的条件下，其产生该观测的对应的状态的概率是多少，而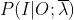恰好就是这个意思，而且随着我们后面的推导，该式子就是我们最终要计算的核心。
（2）-（3）：这一步用到了关键一步-Jessen不等式，我们这里用到的最重要的就是Jessen不等式的结论：
如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])，通俗的说法是函数的期望大于等于期望的函数。
特别地，如果f是严格凸函数，当且仅当P(X = EX) = 1，即X是常量时，上式取等号，即E[f(X)] = f(EX)。
当f是（严格）凹函数，当且仅当-f是（严格）凸函数，不等号方向反向，也就是E[f(X)]<=f(E[X])
因为log是凹函数，所以对应公式中通俗点讲就是数学期望的log大于等于log的数学期望。
因为Jessen不等式是个纯数学知识，关于该不等式的定理，这里不再赘述了，可以参考通俗理解EM算法，博客里对对该公式在EM算法中的用法写的很清楚了哈。当然也可以自行搜索资料，网上一堆。
接着来看（3）后半部分，比（2）多了
，为啥多了这个呢？因为我们有（3）到（4）的变换；
（3）-（4）：在（4）中，我们把减号的前后两个部分合在了一起，归功于（3）中后半部分的，这样一来，就可以根据log的计算法则将减法变成除法了，这里为啥可以这样？因为P(I|O;λ)本身是个条件概率，求的是在O已知条件下，I取各个值的概率，既然如此，对I取所有可能值的概率之和必然是1，即
。这里可能有人要问了，凭啥后头的是1，前面的那个不也是1，这样的话不用在后面补上这个求和，只需要把前面的这个求和去掉就行了啊！注意哈，前面的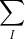
还和log里的I关联的，所以这里是不可以简单等于1的。那么你又要问了，既然∑是对包含log的那一堆而言的，那就不能和后半部分的提取公因式啊！这里又要注意，∑的底数是I，I=i1,i2,...,iN，我们其实是对每个i进行计算的，也就是当I=i1时，有
单例情况下，我们可以提取公因式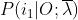
得到
同理，I=i2时，同样可以提取
，以此类推，然后求和后，总的就可以写成（4）的形式了。我觉得我已经讲的够明白了==
至此，我们把EM算法最核心最难懂的部分讲完了。因为我们要求得是当前时刻的λ，即求解L(λ)，所以我们来看下它是多少。
通过上面的分析，我们得到这么一个式子：
对吧，而我们上面说了， 是个已知量，又观察9.14，现在我们的已知量有、O，未知量是I，而当O作为已知条件时，条件概率P(I|O;)可求，所以整个 P(I|O;)也是已知的。通过这个分析，我们可以把9.14再简化一下：
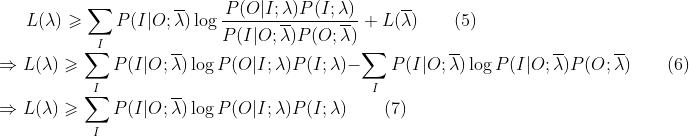注意这里有个细节，我们不能简单的在（5）式中，直接将所有的 P(I|O;) 抹去，虽然它是个已知量，但是这里它和log是相乘的关系，且log里的分子是未知量，且整体和前面的∑相关，就好比∑后面的那个P(I|O;)是log的系数，肯定是不可以简单去掉的。L>=2x+3y，你能简单的把它简化成L>=x+y吗？显然不行，所以从（5）到（6）我们做了一个log展开，展开后就明朗了，（6）中的后半部分全部都是已知量，所以直接消除，就剩下前半部分了，于是就得到了（7）。
高中的时候我们学过，要让
恒成立，只需要让后者的最大值仍然小于前者就行，所以我们这里其实就需要求解
也就是说，通过求解极大化似然函数来估计促使该似然函数极大化的参数。令
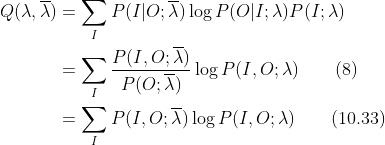
那么
上述的Q其实就是所谓的EM算法中的Q函数。另外，之所以有（8）式到10.33式的变换，实际就是条件概率和联合概率的转化公式，即P(A|B)=P(A,B)/P(B)，而P(O;)已知，故消去。至此，我们也详细推导了《统计学习方法》中10.33式是怎么来的，也顺手复习了一下EM算法。
总结一下，我们先由定义出发，写出了含有隐变量的完全数据的对数似然函数式，又从极大化似然函数的思想出发， 写出了迭代式，即每次迭代都比上次计算结果大，从而一步步推导出Q函数。式9.17实际上是一次迭代，该次迭代用到了上次迭代计算得到的参数，所以我们每一次极大化Q得到的都能够反哺计算出更大的Q对应的λ，而首次迭代用到的λ需要我们初始化得到。
四、Baum-Welch算法的参数估计（重要核心）
通过EM算法的重温，我们发现了，Baum-Welch算法要解决的问题就是EM算法要解决的问题，就是对10.33式的参数的极大化似然估计。在隐马尔科夫模型中，我们的λ包括π、A、B，也就是我们需要通过10.33式来估计出这三个参数。从隐马尔科夫模型计算问题中我们得到：
所以，
于是，极大化Q函数实际上就是分别极大化
1. π的估计
先来看下第一项：
其中，
，我们回忆一下概率计算问题中的那个例子，例子中对于每一个盒子代表每一个状态，初始状态下，π表示初始状态的概率分布，即选取每一个盒子的概率分别为多少，那么这些概率的和即为1。现在有了这个条件的限制，那么求解上式就不再是一个简单的无约束问题了，而是一个带约束的极大化问题，所以我们很自然的想到用拉格朗日乘子法来求。
首先，我们把I展开：
这么变换的原理是因为我们的I表示i1, i2, ..., iT，而π只在初始状态有效，所以只取状态i1，又因为i1可取i=1到i=N这N种状态值，所以对I的求和需要变成从i=1到N的求和，所以我们的i1就可以写成i，注意it中的i和单独的那个i是不一样的，前者包含了所有N个状态值，后者是单独一个状态值的表示，本来为了避免歧义，我这里用qi表示每个状态，但为了后续公式敲打方便，下面qi我统一写成i：
通过约束条件构建拉格朗日函数：
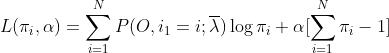
常规操作，L对π求偏导，并令导数为0，求得α：
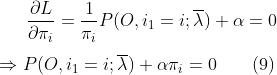
注意这里的细节：之所以求偏导后求和符号不见了，这是因为在求和符号中，我们是对i取每个值而言的，如果将求和符号展开成多项式求和，那么我们求偏导就是得在i取不同值的情况下分别求偏导，当i取某个值的时候，多项式中其它项均为常数，求导为0，举个例子，对
求a的偏导，我们先把它展开：
所以，
所以
可表示为：
这就解释了为啥求偏导后∑没有了，对于这个细节，全网找不到解释，显得公式推导解释很不完整。虽然这是个基础，但是我觉得对于非数学科班的人来说，还是有必要解释一下的。
好了，让我们回到（9）式，现在要想办法消掉π，我们知道，，所以对（9）式两边求和，得到
（10）式的求和符号没有了是因为联合概率对I求和后会得到关于O的边缘概率。这种变化如果不懂的小伙伴参考这里。常规操作，我们把（10）式带回到（9），得到
这样我们就得到了π的表达式（11）。
2. A的估计
现在我们来看一下第二项：
同样，我们有
，即不管i是多少，所有的j的可能状态值的概率之和为1，在之前那个例子中，即A矩阵的每一行之和，就是对于当前时刻的某个盒子，转移到下一时刻所有盒子的可能性之和为1。 同样是带约束问题，为了求导方便，我们需要把a中的t消去：
因为我们的t从1到T-1中取任意一个时刻时，都对应一个状态it，每一个it又可以取i=1~N种状态值，所以原本我们除了最后一个∑外，前面的那几个∑都可以写成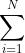
，但是我们注意到a的下标是两个，表示当前时刻的状态为it时转移到下一时刻的状态为
，这两个时刻的状态都有N种可能的状态值，所以这里我们需要再添加一个∑符号表示转移到下一时刻状态的可能取值：
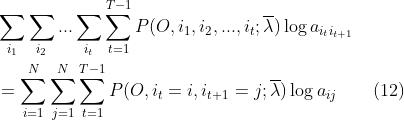
（12）就是我们待求解的形式，这个变换有些复杂，有限篇幅传达解释往往无法面面俱到，但是非常之重要，有看不懂的小伙伴请及时在评论区留言！
同求解π一样，我们构造拉格朗日函数：
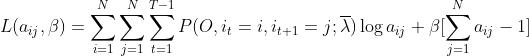
L对aij求偏导，并令偏导为0：
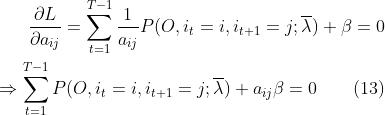
关于为啥求导后∑没了，这个我上面应该讲的很清楚了。因为我们的 ，所以对（13）式进行求和：
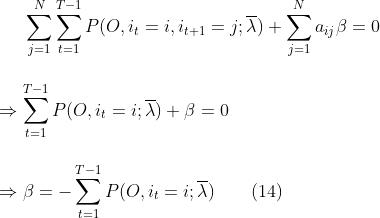
a的∑没了好理解，那么P关于j的∑咋也没了呢？因为关于j求和后，相当于P中的j已经取得所有可能性了，这个时候就和j没有关系了，所以可以把j消掉。常规操作，求得的β带回到（13）式中，得到：
这样我们就得到了aij的表达式（15）。
3. B的估计
我们来看最后一项，这一项比较麻烦，铁友们，我们再坚持一下：
与上面相同，该项也是一个带约束的问题，其约束项为：
和前面有些不同，这里是k有M种可能得观测值，因为这里的b是观测概率矩阵，也就是每个盒子中取得白球和红球的概率，显然白球和红球的概率之和为1。
同样，为了求导方便，我们需要展开一下：
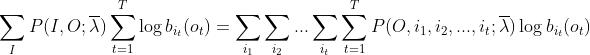
这里在展开讲一下：
当t=1时，我们取的是
，
取值为
，
取值为
，
；
当t=2时，我们取的是
，
取值为
，
取值为
...
不管t取多少，都有对应的it取值为1到N种可能的状态值，注意看b的下标也为it，所以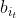
应写成
，i取值为1到N种可能的状态值。所以上式可以转换成：
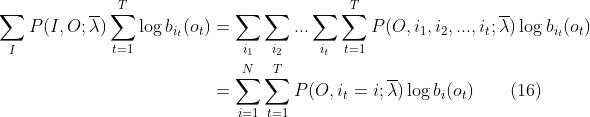
总之记住，每次只取一个状态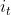
，每个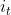
都有1到N种可能的状态值。同样的，因为某一状态下产生所有观测值的概率之和为1，所以有
这里b中的ot改写成k是因为对于每一个状态下，ot已经是对应状态下的一个观测变量，该观测变量是由M个可能的观测值组成的，所以没必要写成ot了，用k表示某一个观测值就行。那么好了，这又是一个带约束的问题，同样可以用拉格朗日函数来求解：
常规操作，L对b求偏导并令导数为0：
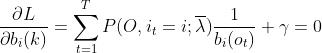
注意这里对b的参数估计有个非常不一样的地方，因为我们的观测值是个已知量，所以对于每个ot（ot=k=1，2，...，M）来讲，k取哪个值是确定的，未知的是那个i，这说明了对b求偏导的时候，只有在ot取得确定值vk的时候才有意义，对于ot取其它值时，上式固然是0。更近一步的解释，在之前的那个盒子取球的例子里，我们看下B矩阵：
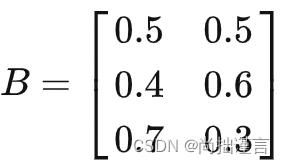
上面那段话的意思就是说，对于每一个状态，我们取B的哪一列是已知的，例如，假设当前观测值为白球，那么在盒子2的状态下， 我们一定取的是第2行底2列，其它列的可能性为0，在盒子3的状态下必然取第3行第2列，其它列的可能性为0，盒子1的状态亦如是。好了，经过上述分析，我们如何能够表示出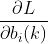
是对ot=vk而言的呢，即偏导不为0？很简单，只需要加个指示函数I即可：
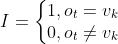
所以，
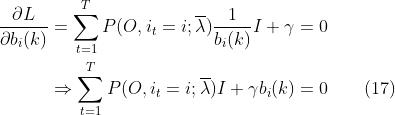
又因为，所以我们对（17）求和：
中间那个式子中I不见了，是因为我们对指示函数I进行，而k从1到M中只有一个值才满足I=1，因此就可以把和I都去掉。常规操作，把（18）带回到（17）得：
至此，我们利用Baum-welch算法把模型参数π、A，B都估计出来了。注意上述（11）、（15）、（19）只是针对1次计算而言的，在我们的算法迭代中，是需要不断更新参数的，即我们每次迭代计算新的λ，都需要用到上次得到的λ，而最初始的λ是我们初始化赋值得到的。
那么我们推出了π、A、B的表达式后，具体怎么计算呢？毕竟上面一堆公式，都是用P来表示的，所以这些P应该等于啥呢？接下去看。
五、Baum-welch算法计算流程
通过第四节我们得到参数估计的公式如下：
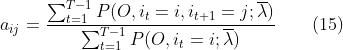
回忆一下 前向算法和后向算法 文章中介绍的概念：
前向概率：
后向概率：
以时刻t为节点，t时刻往前的为到时刻t的这部分观序列的前向概率，t时刻往后的为t到T时刻这部分观测序列的后向概率，所以，它们联合起来就是：
机器学习算法之——隐马尔可夫模型(Hidden Markov Models,HMM) 代码实现
EM算法(Expectation Maximization Algorithm)详解(附代码)---大道至简之机器学习系列---通俗理解EM算法。
机器学习算法之——隐马尔可夫(Hidden Markov ModelsHMM)原理及Python实现