等式约束优化问题
Posted oliveQ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了等式约束优化问题相关的知识,希望对你有一定的参考价值。
等式约束优化问题
等式约束的基本定义
-
等式约束问题
min f ( x ) , s . t . A x = b , A ∈ R p × n , r a n k ( A ) = p \\minf(x),s.t. Ax=b,A\\isin R^p\\times n,rank(A)=p minf(x),s.t.Ax=b,A∈Rp×n,rank(A)=pf是凸函数,二次可微,假设 p ∗ p^* p∗是存在且确定的, p < n p<n p<n,即约束条件小于变量维数,可以存在多解,否则可能会无解
-
等式约束的对偶问题
拉格朗日函数: L ( x , ν ) = f ( x ) + ν T ( A x − b ) L(x,\\nu)=f(x)+\\nu^T(Ax-b) L(x,ν)=f(x)+νT(Ax−b),设最优点 x ∗ x^* x∗由此得到KKT条件方程组 A x ∗ = b ∇ f ( x ∗ ) + A T ν ∗ = 0 \\begincasesAx^*=b \\\\ \\nabla f(x^*)+A^T\\nu^*=0 \\endcases Ax∗=b∇f(x∗)+ATν∗=0
x ∗ 是 最 优 点 , ν ∗ 是 对 偶 最 优 点 , p ∗ = inf x f ( x ) ∣ A x = b = f ( x ∗ ) x^*是最优点,\\nu^*是对偶最优点,p^*=\\inf_x\\f(x) | Ax=b\\=f(x^*) x∗是最优点,ν∗是对偶最优点,p∗=infxf(x)∣Ax=b=f(x∗)
-
例子:二次规划问题
min 1 2 x T P x + q T x + r A x = b ⟹ A x = b P x + q + A T ν ∗ = 0 \\begincases\\min\\frac12x^TPx+q^Tx+r \\\\ Ax=b \\endcases\\implies\\begincasesAx=b \\\\ Px+q+A^T\\nu^*=0 \\endcases min21xTPx+qTx+rAx=b⟹Ax=bPx+q+ATν∗=0
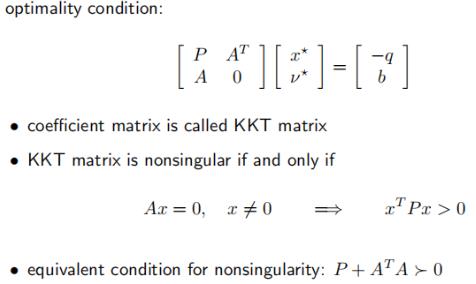
前一个左边的矩阵 ( n + p ) × ( n + p ) (n+p)\\times(n+p) (n+p)×(n+p),复杂度是 O ( ( n + p ) 3 ) O((n+p)^3) O((n+p)3)
二次规划问题仅求导一次就可以实现KKT条件,所以- 牛顿法(迭代步需要求二阶导):利用二次函数(存在海森矩阵)去逼近普通函数(下文的目标)
- 梯度下降法:利用一次函数(存在导数)去逼近普通函数
消除等式约束
-
通过变量替换实现等式消除
-
变量替换 x ∗ = F z ∗ + x ^ x^*=Fz^*+\\hatx x∗=Fz∗+x^
若 x ^ \\hatx x^是任意的一个特解,那么可以实现变换 x ∣ A x = b = F z + x ^ ∣ z ∈ R ( n − p ) \\x|Ax=b\\=\\Fz+\\hatx|z\\isin R^(n-p)\\ x∣Ax=b=Fz+x^∣z∈R(n−p)
于 是 得 到 A ( F z + x ^ ) = b ⟹ A F z = 0 ⟹ A p × n F n × ( n − p ) = 0 于是得到A(Fz+\\hatx)=b\\implies AFz=0\\implies A_p\\times nF_n\\times(n-p)=0 于是得到A(Fz+x^)=b⟹AFz=0⟹Ap×nFn×(n−p)=0
于是A的行组成空间与F的列组成空间正交,即A的零空间就是F的值空间。
min f ( x ) , s . t . A x = b ⟺ min z F ^ ( z ) = f ( F z + x ^ ) \\minf(x),s.t. Ax=b \\iff \\min_z \\hatF(z)=f(Fz+\\hatx) minf(x),s.t.Ax=b⟺minzF^(z)=f(Fz+x^)【把等式约束加到目标函数里,变成无约束问题】
-
求解对偶最优解 ν ∗ \\nu^* ν∗
原问题的KKT系统: ∇ f ( x ∗ ) + A T ν ∗ = 0 \\nabla f(x^*)+A^T\\nu^*=0 ∇f(x∗)+ATν∗=0,同时左乘矩阵A(实现满秩运算)
得到 ν ∗ = − ( A A T ) − 1 A ∇ f ( x ∗ ) \\nu^*=-(AA^T)^-1A\\nabla f(x^*) ν∗=−(AAT)−1A∇f(x∗)
验证目标: ∇ f ( x ∗ ) − A T ( A A T ) − 1 A ∇ f ( x ∗ ) = 0 \\nabla f(x^*)-A^T(AA^T)^-1A\\nabla f(x^*)=0 ∇f(x∗)−AT(AA以上是关于等式约束优化问题的主要内容,如果未能解决你的问题,请参考以下文章
优化理论09-----线性等式约束问题的投影方法投影最速下降算法解决方向查找问题(DFP)牛顿法的修正在线性等式约束变度量法
-