07-内点法(不等式约束优化算法)

Posted 2021-06-23 二十三岁的有德

一、简介 二、对数障碍 三、中心路径 四、障碍方法 五、总结

07-内点法(不等式约束优化算法)

目录

• 一、简介
• 二、对数障碍
• 三、中心路径
• 四、障碍方法
• 五、总结

凸优化从入门到放弃完整教程地址：https://www.cnblogs.com/nickchen121/p/14900036.html

一、简介

这篇文章，我们考虑如下带等式约束和不等式约束的凸优化问题：

\\(\\begin{align} \\min \\quad & f_0(x) \\\\ \\mathrm{s.t.}\\quad & f_i(x) \\leq 0 \\quad i=1, \\cdots, m \\\\ & Ax = b \\end{align} \\tag{1}\\)

其中， \\(f_0, \\cdots, f_m: \\mathbb{R}^n \\mapsto \\mathbb{R}\\) 是二次可微凸函数， \\(A \\in \\mathbb{R}^{n \\times p}, \\mathrm{rank}(A) = n \\leq p\\) 。假设最优解用 \\(x^*\\) 表示，最优值用 \\(f_0(x^*)\\) 表示。

我们还假定该问题严格可行，即存在 \\(x \\in dom(f)\\) 满足 $Ax = b $ 和 \\(f_i(x) < 0, i =1, \\cdots, m\\) 。这意味着存在最优对偶 \\(\\lambda^*, \\nu^*\\) 满足KKT条件(KKT条件的介绍，参见KKT条件：

\\(\\begin{align} f_i(x^*) &\\leq 0, \\quad i = 1, \\cdots, m \\\\ h_i(x^*) &= 0, \\quad i = 1, \\cdots, p \\\\ \\lambda_i^* &\\ge 0, \\quad i = 1, \\cdots, m \\\\ \\lambda_i^* f_i(x^*) &= 0, \\quad i = 1, \\cdots, m \\\\ \\nabla f_0(x^*) + \\sum_{i=1}^m \\lambda_i^* \\nabla f_i(x^*) + \\sum_{i=1}^{p} \\nu_i^* \\nabla h_i(x^*) &= 0 \\end{align} \\tag{2}\\)

所以用内点法求解问题(1)，就等价于求解问题(2)。显然直接求解(2)是非常困难的，所以我们采用一定的技巧(障碍法)，将不等式约束加入到目标函数，从而使问题转化为带等式约束的凸优化问题，从而可以利用无约束凸优化问题求解——Newton Method介绍的办法进行求解。

二、对数障碍

我们重新表述问题(1)，将其转化为等式约束问题：

\\(\\begin{split} \\min \\quad & f_0(x) + \\sum_{i=0}^m I_{-}(f_i(x)) \\\\ \\mathrm{s.t.} \\quad & Ax = b \\end{split} \\tag{3}\\)

其中 \\(I_{-}: \\mathbb{R} \\mapsto \\mathbb{R}\\) 是非正实数的示例函数，

\\(I_{-}(x) = \\begin{cases} 0 & \\textrm{ if} \\,\\, x \\leq 0 \\\\ \\infty & \\textrm{otherwise} \\end{cases} \\\\\\)

注：这里做这样的转换，是因为如果 \\(f_i(x)\\) 不成立，则目标函数的解为无穷大，即无解；反之，由于 \\(I\\_(x)=0\\) 不会对原问题的解造成任何影响。

但是可以看到 \\(I_{-}(x)\\) 是不可微的函数，不能直接应用Newton Method。但是，我们可以近似示例函数：

\\(\\hat{I_{-}}(x) = \\phi(x) =- (1/t) \\log(-x), \\quad dom(\\hat{I_{-}}) = - \\mathbb{R}_{++} \\\\\\)

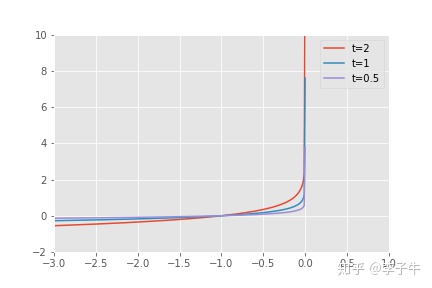对数障碍函数。t越大，精度越高，越接近示例函数。注：这里有点机器学习中利用 sigimoid 函数替代 sign 函数的味道

可以看到上面的近似函数，其是可微的凸函数。下面我们求解如下近似问题，并且我们将给予证明当 \\(t \\to \\infty\\) 时，近似问题的解与原问题的解是一样的。

\\(\\begin{split} \\min \\quad & f_0(x) + \\sum_{i=0}^m -(1/t) \\log(-f_i(x)) \\\\ \\mathrm{s.t.} \\quad & Ax = b \\end{split} \\tag{4}\\)

为了方便以后讨论，我们定义 \\(\\phi(x) = -\\sum_{i=1}^m \\log(-f_i(x))\\) 为对数障碍函数 ，并直接给出其梯度和Hessian矩阵。

\\(\\nabla \\phi(x) = \\sum_{i=1}^m \\frac{1}{-f_i(x)} \\nabla f_i(x) \\\\\\)

\\(\\nabla^2 \\phi(x) = \\sum_{i=1}^m \\frac{1}{-f_i(x)} \\nabla^2 f_i(x) + \\sum_{i=1}^m \\frac{1}{f_i(x)^2} \\nabla f_i(x) \\nabla f_i(x)^T \\\\\\)

三、中心路径

下面我们考虑如何求解问题(4)，为了简化符号表达，对目标函数乘以 \\(t\\) ，考虑如下等价问题：

\\(\\begin{split} \\min \\,\\quad &t f_0(x) + \\phi(x) \\\\ \\mathrm{s.t.} \\,\\quad & Ax = b \\end{split} \\tag{5}\\)

对任意的 \\(t > 0\\) ，上述优化问题存在唯一的最优解 \\(x^*(t)\\) ，将这一系列最优解组成的集合 \\(\\{x^*(t)\\}\\) 称为中心路径。注：前面说到 \\(t\\) 是不确定的，因此这一系列解就是不同的 \\(t\\) 对应的最优解，中心路径上的点满足 \\(x^*(t)\\) 是严格可行的，即：

\\(Ax^*(t) = b, \\quad f_i(x^*(t))<0, \\quad i =1, \\cdots, m \\\\\\)

并且存在 \\(\\hat \\nu \\in \\mathbb{R}^p\\) 使得（KKT 条件）

\\(\\begin{align} 0 &= t \\nabla f_0(x^*(t)) + \\nabla \\phi(x^*(t)) + A^T \\hat \\nu \\\\ & = t \\nabla f_0(x^*(t)) + \\sum_{i=1}^m \\frac{1}{-f_i(x^*)} \\nabla f_i(x^*) + A^T \\hat \\nu \\end{align} \\tag{6}\\)

(6)提供了一个重要的性质：每个中心点产生对偶可行解，从而给出最优值 \\(p^*\\) 的一个下界。更确切地说，定义

\\(\\lambda^*(t) = - \\frac{1}{tf_i(x^*(t))}, \\quad i =1, \\cdots, m, \\quad \\nu^*(t) = \\hat \\nu/t \\tag{7}\\)

我们要说明 \\(\\lambda^*(t), \\nu^*(t)\\) 是原问题(1)的对偶可行解。

首先验证 \\(\\lambda^*(t) >0\\) ，这点由 \\(f_i(x^*(t)) < 0\\) 保证。其次，我们重新整理(6)（注：公式 (6) 除以 \\(t\\)）得到：

$ \\nabla f_0(x^(t)) + \\sum_{i=1}^m \\lambda^(t) \\nabla f_i(x^) + A^T \\nu^(t) = 0 \\ $注：从这里就可以看出 KKT 条件的影子

因此 \\(x^*(t)\\) 使得 \\(\\lambda = \\lambda^*(t), \\nu = \\nu^*(t)\\) 时的Lagrange函数

\\(L(x,\\lambda, \\nu) = f_0(x) + \\sum_{i=1}^m \\lambda_i f_i(x) + \\sum_{i=1}^p \\nu_i h_i(x) \\\\\\)

达到极小，这意味着 $ \\lambda^(t), \\nu^(t)$是对偶可行解。因此对偶函数 \\(g( \\lambda^*(t), \\nu^*(t))\\) 是有界的：

\\(\\begin{align} g( \\lambda^*(t), \\nu^*(t)) &= f_0(x^*(t)) + \\sum_{i=1}^m \\lambda^*(t) f_i(x^*) + \\nu^*(t)^T(Ax^*(t) - b) \\\\ &= f_0(x^*(t)) - m /t \\\\ \\end{align} \\\\\\)

即，近似解 \\(g( \\lambda^*(t), \\nu^*(t))\\) 与原问题最优解 \\(p^*\\) 之间的间隙就是 $m/t $ 。随着 \\(t \\to \\infty\\) ， \\(m/t \\to 0\\) 。

\\(g( \\lambda^*(t), \\nu^*(t)) \\leq p^* \\Rightarrow f_0(x^*(t)) -p^* \\leq m/t \\\\\\)

注：上述就是通过对可行解的分析，得出近似解和原问题的最优解的差值

这里，我们补充给出基于KKT条件的解释。
我们可以将中心路径条件(6)解释为KKT最优性(2)的变形。
点 \\(x\\) 是等于 \\(x^*(t)\\) 的充要条件是存在 \\(\\lambda, \\nu\\) 满足
\\(\\begin{align} Ax = b, \\quad f_i(x) &\\leq 0, \\quad i=1, \\cdots, m \\\\ \\lambda_i &\\ge 0, \\quad i=1, \\cdots, m \\\\ \\nabla f_0(x) + \\sum_{i=1}^m\\lambda_i f_i(x) + A^T\\nu &= 0 \\\\ -\\lambda_i f_i(x) &=1/t, \\quad i=1, \\cdots, m \\end{align} \\tag{8}\\)
近似问题的KKT条件(8)与原始KKT条件(2)的唯一的差别是 \\(-\\lambda_i f_i(x) =0\\) 被 \\(-\\lambda_i f_i(x) =1/t\\) 替代注：这里来自于我们对公式 (6) 的处理。特别地，当 \\(t\\) 很大时， \\(x^*(t)\\) 和对应的对偶解 \\(\\lambda^*(t), \\nu^*(t)\\) "几乎"满足原始问题(1)的KKT条件。

这里小结一下。我们在中心路径这部分给出了证明近似问题(5)的最优解与原始问题(1)的最优解的误差不超过 \\(m/t\\) ，因此我们可以放心的求解近似问题(5)。

四、障碍方法

下面给出Newton Method求解近似问题(5)的算法框架

重复进行：

1. 中心点步骤：从初始值 \\(x\\) 开始，采用Newton Method在 \\(Ax=b\\) 的约束下极小化 \\(tf_0 + \\phi\\) ，最终确定 \\(x^*(t)\\)
2. 改进： \\(x:= x^*(t)\\)
3. 停止准则。 如果 \\(m/t < \\epsilon\\) 则退出
4. 增加 \\(t\\) ： \\(t:= \\mu t, \\quad \\mu>1\\)

根据在中心路径小节中的分析，近似问题(5)的最优解与原始问题(1)的最优解的误差不超过 \\(m/t\\)，所以在求解时，我们从较小的 \\(t\\) 开始，不断增大 \\(t\\) 直至收敛。此外，我们把每次求出的最优解 \\(x^*(t)\\) 当作下一个 \\(t:= \\mu t\\) 的初值，这样Newton Method会收敛更快，即Step1.中心点步骤的运行时间可以当作常数对待，而不是一个耗时的迭代循环。

五、总结

在这篇文章里，我们介绍了带等式约束和不等式约束的凸优化问题。通过引入对数障碍函数，我们把原问题近似为带等式约束的凸优化问题，从而可以应用Newton Method求解KKT最优条件，找到最优解；此外，我们也给出了近似问题的最优解和原问题的最优解之间的误差，证明当 \\(t\\) 不断增大时，精度会不断提高。

到这里，整体凸优化系列已经全部讲完了。对于最简单的无约束凸优化问题，我们可以采用Gradient Descent或者Newton Method求解；对于稍复杂的等式约束凸优化问题，我们对目标函数进行二阶Taylor近似，然后采用Newton Method求解KKT最优条件；对于最复杂的带不等式约束问题，则时引入对数障碍函数，转化为带等式约束的凸优化问题。

参考文献：Stephen Boyd, Lieven Vandenberghe: Convex Optimization

参考资料：https://www.zhihu.com/column/c_1046701775096188928