深度学习7-矩阵乘法运算的反向传播求梯度

Posted 2022-09-05 清风莫追

🚩 前言

本节以较简单的例子来理解矩阵乘法下的反向传播过程。为了稍微形象一些，这里同样会用到计算图来进行描述。

矩阵乘法下的反向传播，其实和标量计算下的反向传播区别不大，只是我们的研究对象从标量变成了矩阵。我们需要解决的就是矩阵乘法运算下求梯度的问题，而两个矩阵的乘法又可以分解为许多标量的运算。

---

文章目录

• 🚩 前言
• 1. 求梯度的公式
• 2. “举个栗子”：两个矩阵相乘
• 3. 从计算图看：误差反向传播

---

1. 求梯度的公式

在矩阵乘法的情况下，设有一个特征矩阵为$X$，一个权值矩阵为$W$，输出：$Y=XW$。
如果我们要得到$Y$关于$W$的梯度，则可以使用公式：$dW=X^{\top }dY$
同样的，如果求$Y$关于$X$的梯度，则可以使用公式：$dX=dY{W}^{\top }$

那么，为什么上面的公式确实可以求出我们所需要的梯度呢？

2. “举个栗子”：两个矩阵相乘

我们不妨看看两个简单矩阵相乘的过程，并将目光聚焦到求关于$W$的梯度

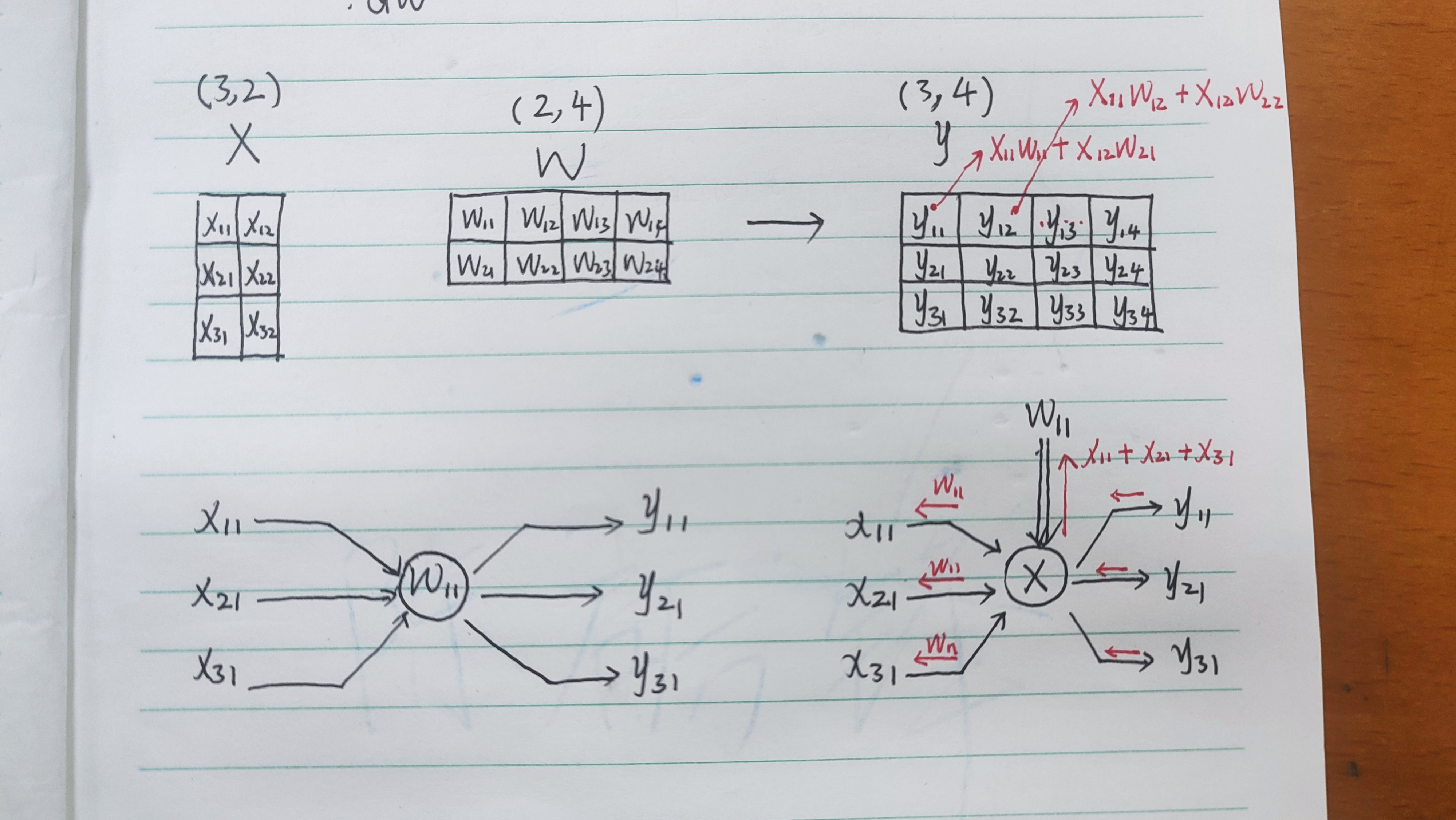
求关于$W$的梯度，则我们得到的$dW$的形状应当是与$W$相同的，即每个元素都有一个对应的梯度。我们看和$W_{11}$有关的部分：

$y_{11}=X_{11}{W}_{11}+X_{12}{W}_{21}$
$y_{21}=X_{21}{W}_{11}+X_{22}{W}_{21}$
$y_{31}=X_{31}{W}_{11}+X_{32}{W}_{21}$

不难发现，$W_{11}$的系数有三个，那么$W_{11}$的梯度就是这三个系数的和：$X_{11}+X_{21}+X_{31}$。

• 对应的系数作为梯度很好理解，可为什么是和呢？而不是平均数？又或者其它的？
  我现在也没有很明白，求得的梯度为什么是它所有系数的和值，主要是对这个梯度值所代表的意义有些困惑。不过平均数其实没有什么意义，不过是给所有求得的梯度等比缩小了而已。

相应的，$W$第一行的元素，其梯度都是$X$第一列的和；第二行的元素，其梯度都是$X$第二列的和。
于是可以发现，通过公式 $dW=X^{\top }dY$，如果$dY$的元素值都为1，我们就恰巧能得到上面的结果。

• 在实际的模型中，矩阵乘法的运算只是作为很小的一个部分，$dY$的值接受自下一层，而非简单的全为$1$，因此不必担心出现每一行的权值只能同步更新的问题

3. 从计算图看：误差反向传播

前面我们是从表达式的系数得出的规律，接下来再从计算图来看一下反向传播求梯度的过程。

• 在考虑神经网络中的误差的反向传播时，计算图确实是一个很棒的工具。对于复杂的矩阵乘法运算，我们可以把它分解成许多简单的加法和乘法运算来考虑。

求W11有关的部分计算图——正向推理

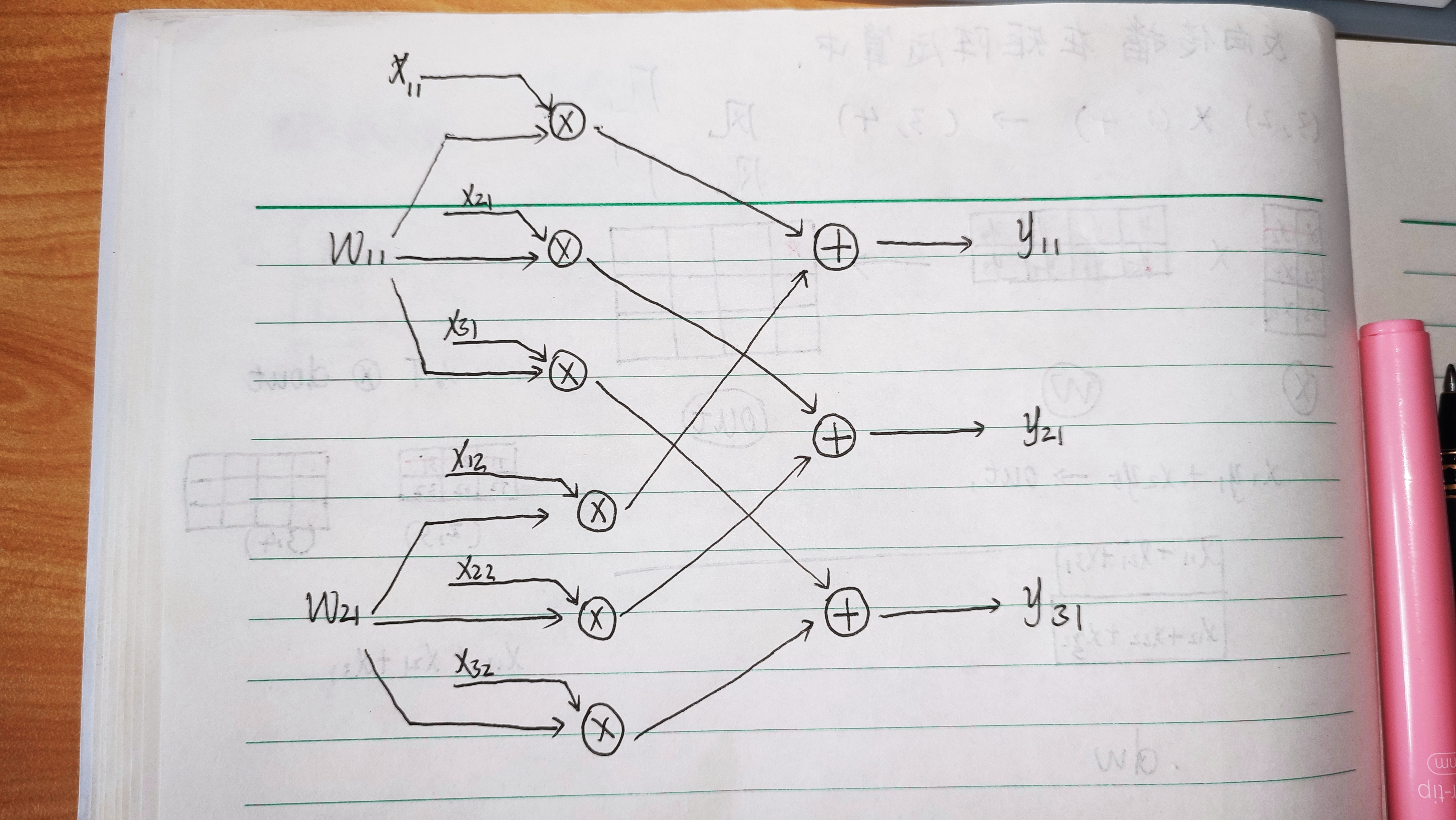
误差反向传播

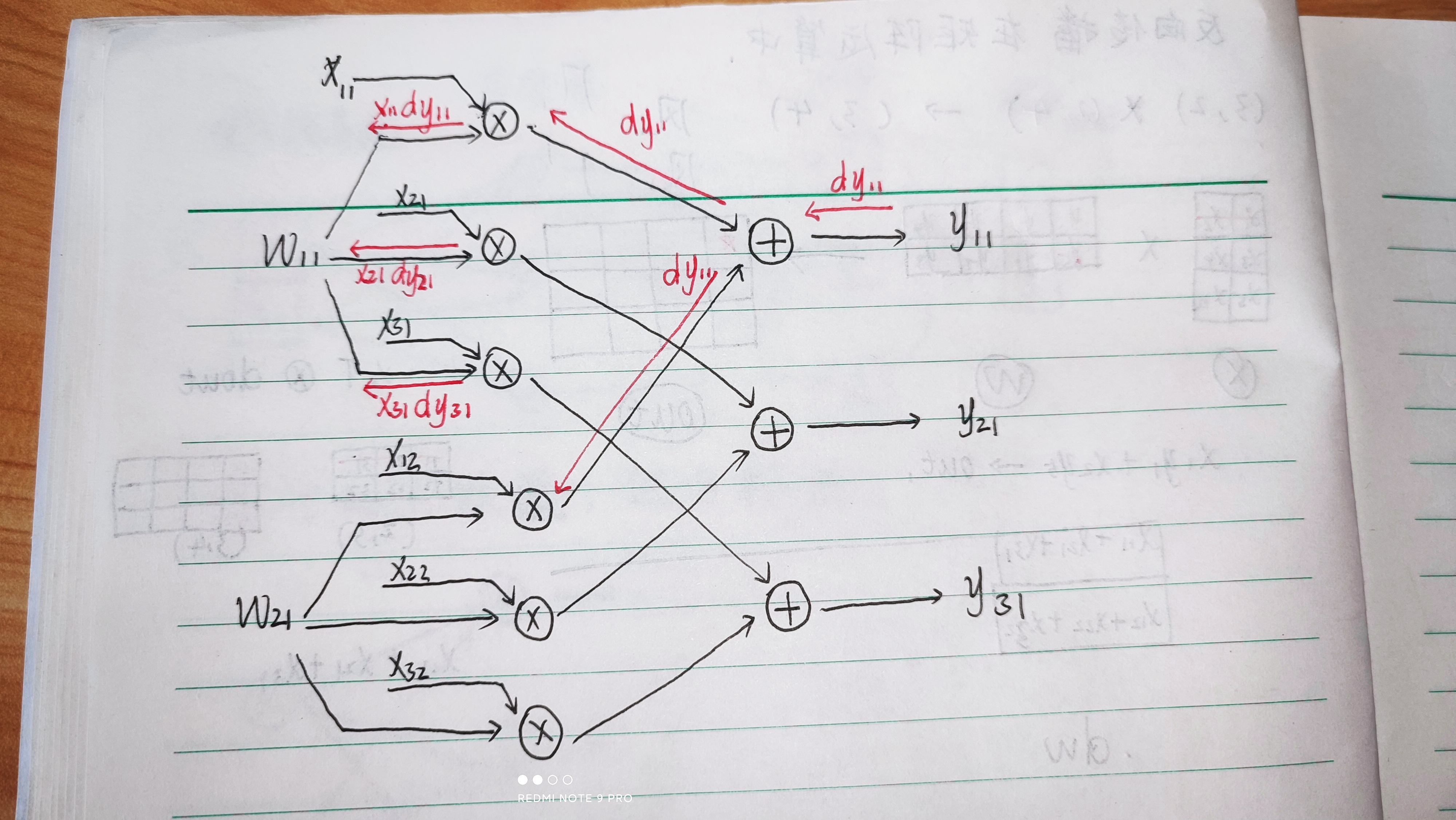
这里我们得到：$d{W}_{11}=X_{11}d{y}_{11}+X_{21}d{y}_{21}+X_{31}d{y}_{31}$

这里只画出了举例子所需要的小部分计算图，将一个矩阵乘法运算完整地用计算图呈现出来，会显得比较错综复杂，也比较麻烦。但使用部分计算图来以点带面、帮助理解还是非常不错的。

---

感谢阅读