[人工智能-深度学习-7]:数据流图正向传播导数梯度梯度下降法反向链式求导,非常非常重要!!!
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[人工智能-深度学习-7]:数据流图正向传播导数梯度梯度下降法反向链式求导,非常非常重要!!!相关的知识,希望对你有一定的参考价值。
作者主页:文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120258939
目录
1.1 数据流图(包括原预测函数、正向传播、损失函数、反向传播、梯度下降迭代)
第3章 常见函数的求导:如何通过正向计算的中间值,直接计算, 获得梯度?
第4章 复合函数的链式求导的原理:通过正向计算的中间值,直接计算, 获得复合函数的梯度。
第1章 数据流图与正向传播
1.1 数据流图(包括原预测函数、正向传播、损失函数、反向传播、梯度下降迭代)
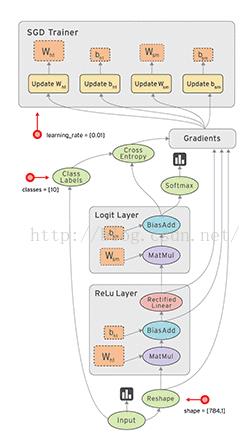
(1)在数据流图的组成
- 叶子节点:就是Wi, Bi的参数。
- 中间节点:就是运算,如加、乘
- “边”就是中间的运行结果
(2)训练的主要步骤:
- 正向传播:在上图中,体现在从input到softmax的中间过程和最终输出过程。
- 反向传播:在上图中,体现在交叉熵和求每个参数的偏导这两个子过程。
1.2 正向传播
(1)子过程1:构建正向传播数据流图 ,即原函数f(x1,x2,....) ,在上图中,体现在Relu层和logit层 + softmax。
上图案例中,正向数据流图的构建如下:
=》ReLuLayer_L0 = X (输入样本)
=》ReLuLayer_L1 = W1 * ReLuLayer_L0 = W1 * X
=》ReLuLayer_L2 = ReLuLayer_L1 + B1 = W1 * X + B1
=》ReLuLayer_L3 = Relu (ReLuLayer_L2) = Relu (W1 * X + B1)
=》Logit_L0 = ReLuLayer_L3
=》Logit_L1 = W2 * Logit_L0
=》Logit_L2 = Logit_L1 + B2 = W2 * Logit_L0 + B2
=》Logit_L3 = softmax(Logit_L2)= softmax(W2 * Logit_L0 + B2)
最终的输出:
Yi = f(Xi) = softmax(W2 * (Relu (W1 * Xi + B1)) + B2)
(2)子过程2:进行“正向传播”,计算“每个边”的中间输出值和最终输出值,在上图中,体现在带箭头的“边”。
正向传播,其实比较简单,也比较容易理解,这个过程就是复合函数的计算过程,并且计算出中间每个“边“的值。
用当前的Wi, Bi的值,带入样本数据Xi, 就可以按照正向的顺序分别计算出每个“边”的值。
1.3 反向传播
(1)子过程1:构建方向传播的数据流图,即loss函数,在上图中,体现在交叉熵。
上图案例中,损失函数的数据流图的构建如下:
f_loss = cross_entropy (Ylable - Yi)
(2)子过程2:进行“反向传播”,求偏导(梯度)
计算Loss函数中每个Wi, Bi的梯度,即偏导数。
偏导数的计算过程并非通过导函数的推导获得,而是直接通过“每个边”的中间输出值,以及所有的叶子节Wi, Bi的值的算术运算得到。这个过程下面再深入探讨。
这里的关键是:
- 原理层面:需要了解反向链式求导的基本原理和过程。这个步骤反向链式求导的理论基础!!!
- 实现层面:如何通过正向计算的结果,直接获取每个变量的梯度值(反向求导的偏导数值),而不需要预先求导函数?这个步骤是自动求导的核心与关键!!!
1.4 梯度下降法迭代,重新回到正向传播过程。
(1)用梯度,对Wi,Bi进行梯度下降法迭代,生成新的Wi和Bi值。
(2)重选的Wi和Bi,与输入样本X,重新进行新一轮的正向传播过程和反向传播过程。
(3)直到Wi和Bi的梯度接近于0,Loss函数为最小值。
第2章 导数与梯度
2.1 什么是一元函数的导数
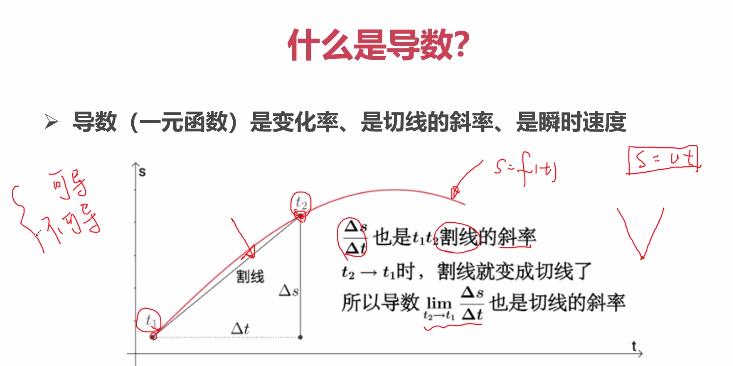
曲线上的有些点是没有导数的,称为不导,如空心点。
曲线上的有些点有两个导数,如上图V字形处。
2.2 什么是多元函数的方向导数
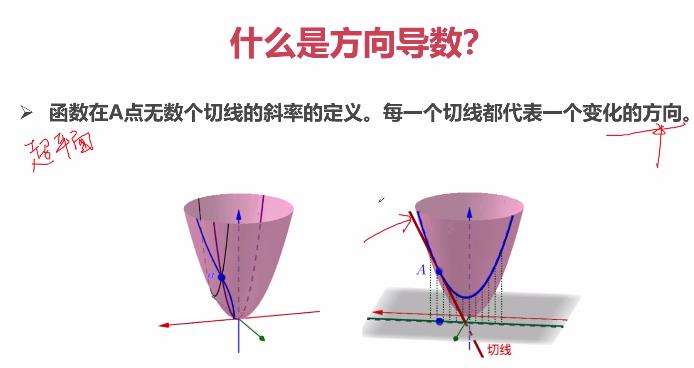
方向导数的方向是无穷多个。
2.3 什么是多元函数的偏导数
为了克服方向导数的无限性带来的不确定性,引入了多元函数的偏导数。
偏导数把方向导数的方向的个数,限制于与多元函数的“元”数完全一致上。
有多少维度的自变量,就有多少个维度的偏导数,并且方向与自变量维度的方向保持一致。

2.4 梯度
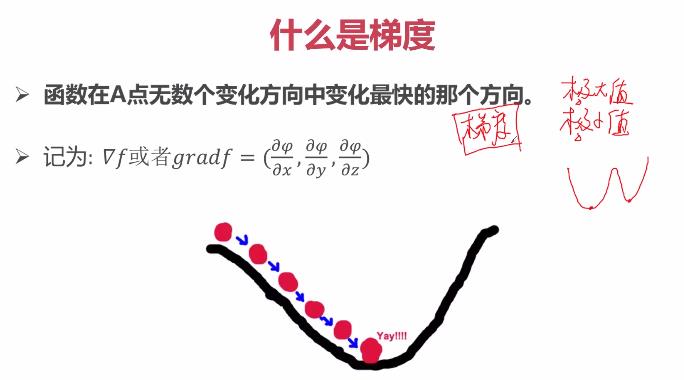

梯度是在机器学习领域引入的一个新的概念,它指明多元函数如何在任意一初始点,通过迭代的方式逐渐收敛于“极小值”的方向。
在具体数学实现时,在某个点处的梯度获取,最终是通该点处的偏导数来实现的。
因此,梯度是机器学习的概念,偏导数是高等数学微积分的概念,大多数时候,这是同一个问题在两个不同层面上的描述。
(1)偏导数是标量,每个偏导数是相互独立的标量。
(2)梯度是向量,是由各个维度上的偏导数组成一个向量。
- 梯度有方向,所有维度方向的向量相加后的方向。
- 梯度有大小,所有维度方向的向量相加后的长度。
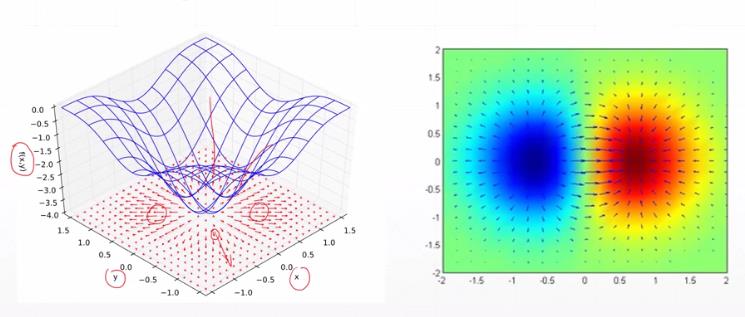
2.5 梯度的作用=》通过梯度下降法求loss函数的极小值
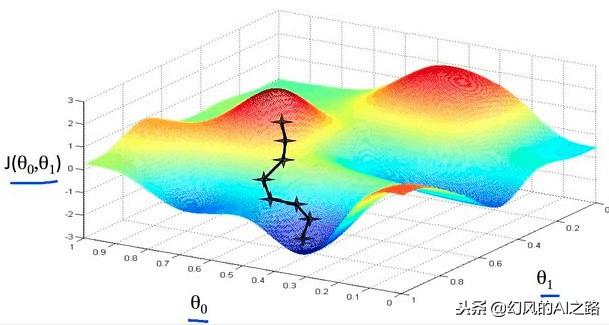
梯度下降算法,我们可以理解为朝着梯度的反方向一点一点的下降,最终我们就能找到损失函数的最小值,此时的模型就是我们所需要的。
下山的过程
比如我们在一座大山上的某处位置(函数的某一位置),由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,这样一步步的走下去,一直走到山脚,这就是梯度下降算法的直观体现。如下图所示:
(1) 一元函数下降过程
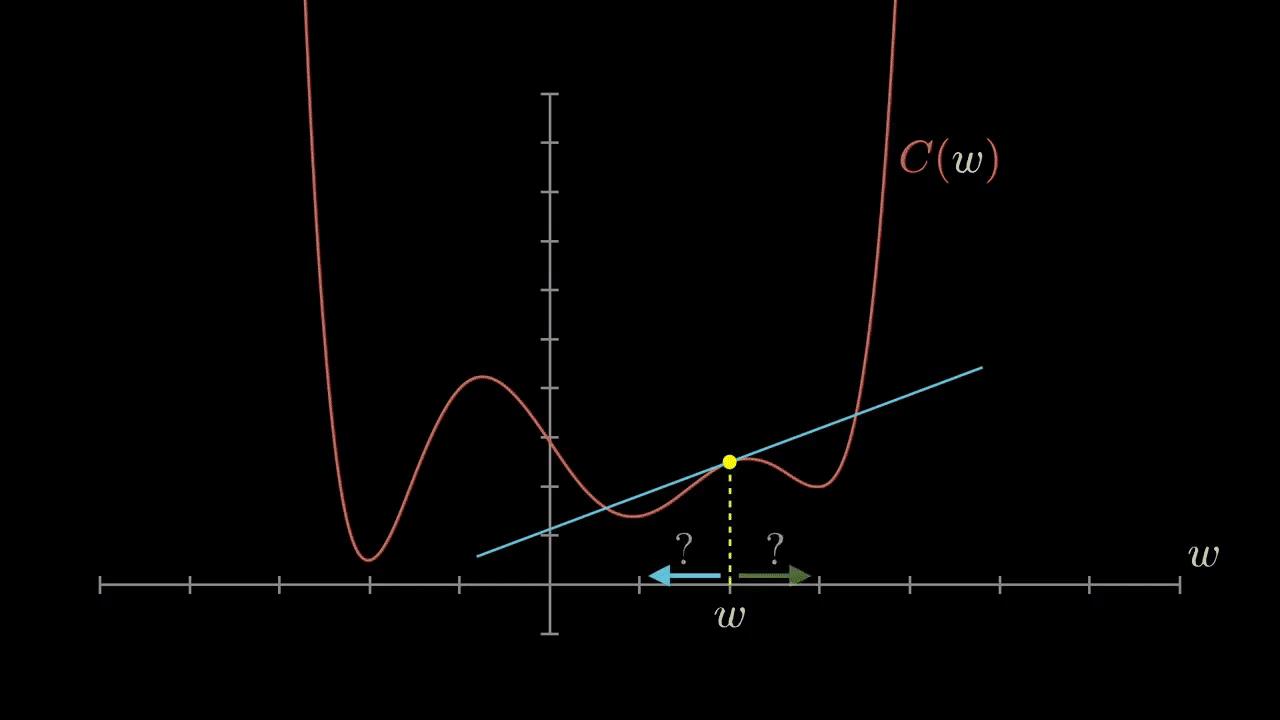
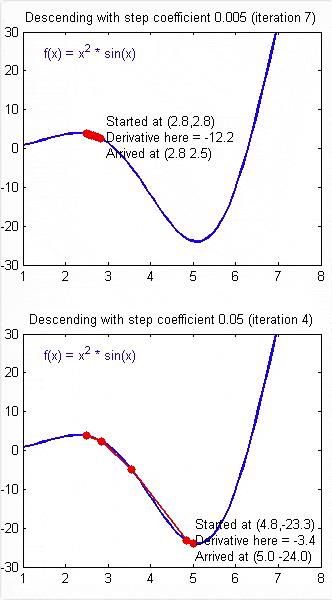
每一次梯度下降的步长 = (-1) * 学习率 * 梯度。
只需要要乘以(-1),是因为迭代的时候,要沿着梯度的反方向进行迭代下降。
只需要要乘以学习率,是因为,梯度是斜率,值很大,为了降低迭代的步长,需要把梯度按比例缩小,学习率通常是0.01或0.001等或其他,总之,通过学习率,对计算出的梯度进行大幅度的按比例缩小,防止迭代的步伐过大,越过极小值点。
学习率的设置非常重要,它决定了每次迭代步长的大小。
步长过小,迭代越精确,但迭代过程过慢。
步长过大,迭代越快,但可能导致迭代越过极小值点,震荡发散,无法收敛。
(2)二元函数梯度下降过程
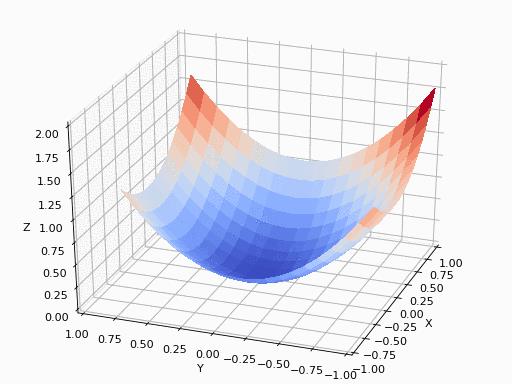
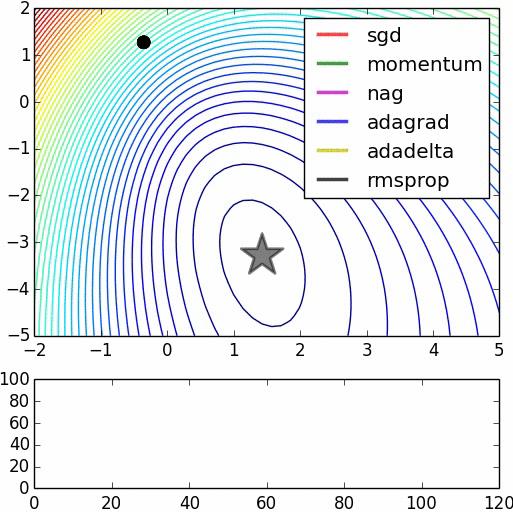
上图展示了不同的迭代算法(优化器)的迭代过程效果。
虽然中间路径不完全相同,但最终都会收敛于极小值。
(3)不同初始值收敛的目标值的影响不同
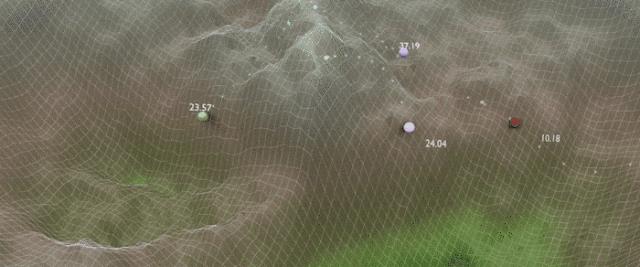
当loss函数,有多个不同的极小值点的时候,不同的初始值,就可能导致收敛到不同的极小值点处,因此,初始值的设定非常重要。
梯度下降的关键是每次迭代的梯度的计算,即偏导数的计算。
第3章 常见函数的求导:如何通过正向计算的中间值,直接计算, 获得梯度?
3.1 技术背景
一般情况下,要求函数在某一个点处的偏导数,需要先获得该函数的导函数,然后根据导函数计算获得该点处的导数。这是一般求导数的方法。
自动求导数/梯度的过程,不需要计算原函数的导函数,根据神经元的线性的特点和激活函数的特点,可以根据原函数的正向传播的中间节点值,直接计算得到某点处的导数值。
原理推导如下;
3.2 线性函数导数与偏导数
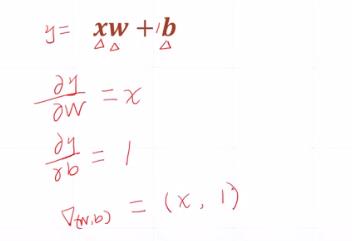
y_loss = f(W,B) = W*Xi + B
W和B对y_loss求偏导数,可以根据原函数的数值直接获得的:
- W的偏导数= Xi
- B的偏导数 = 1
Xi可通过样本标签可以获得,连正向传播都不需要。
3.3 二次函数导数与偏导数
(1)案例1
y_loss = f(W,B) = (W*Xi + B - Yi)^2
W和B对y_loss求偏导数,可以根据原函数的数值直接获得的:
- W的偏导数= 2*(W*Xi + B - Yi)* Xi
- B的偏导数 = 2*(W*Xi + B - Yi)* 1
其中:
W*Xi + B可以通过正向传播可以获得,
Xi, Yi可通过样本标签可以获得。
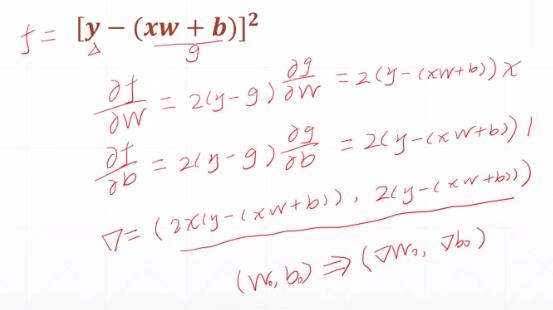
(2)案例2
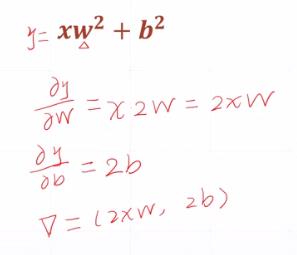
3.4 指数求导
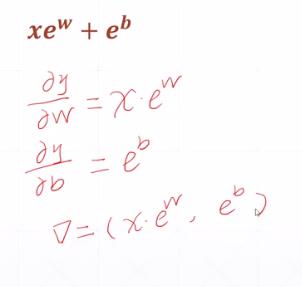
w和b位于指数位置,其梯度也可以直接通过计算原函数获得。
3.5 对数求导
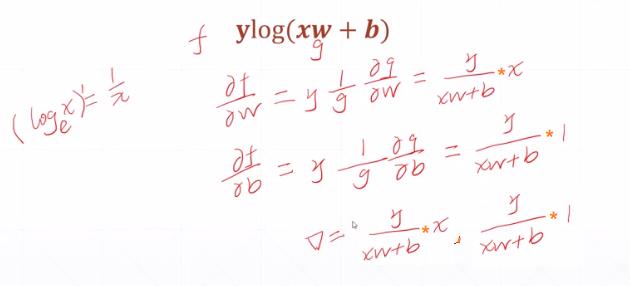
3.6 常见的激活函数的导数
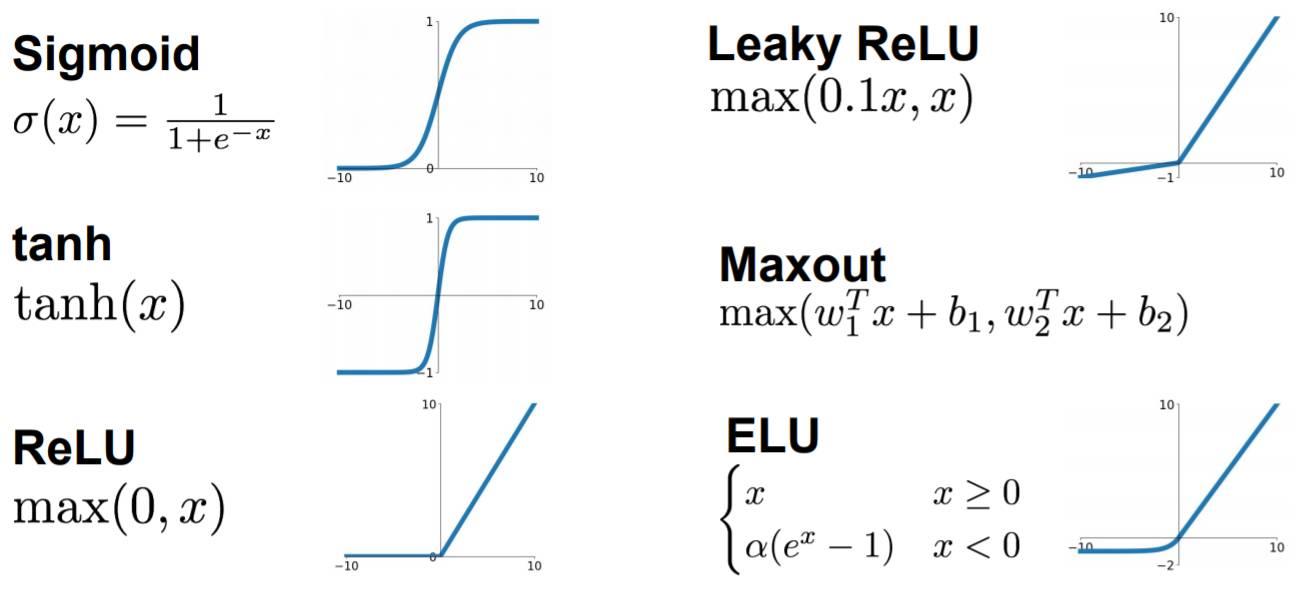
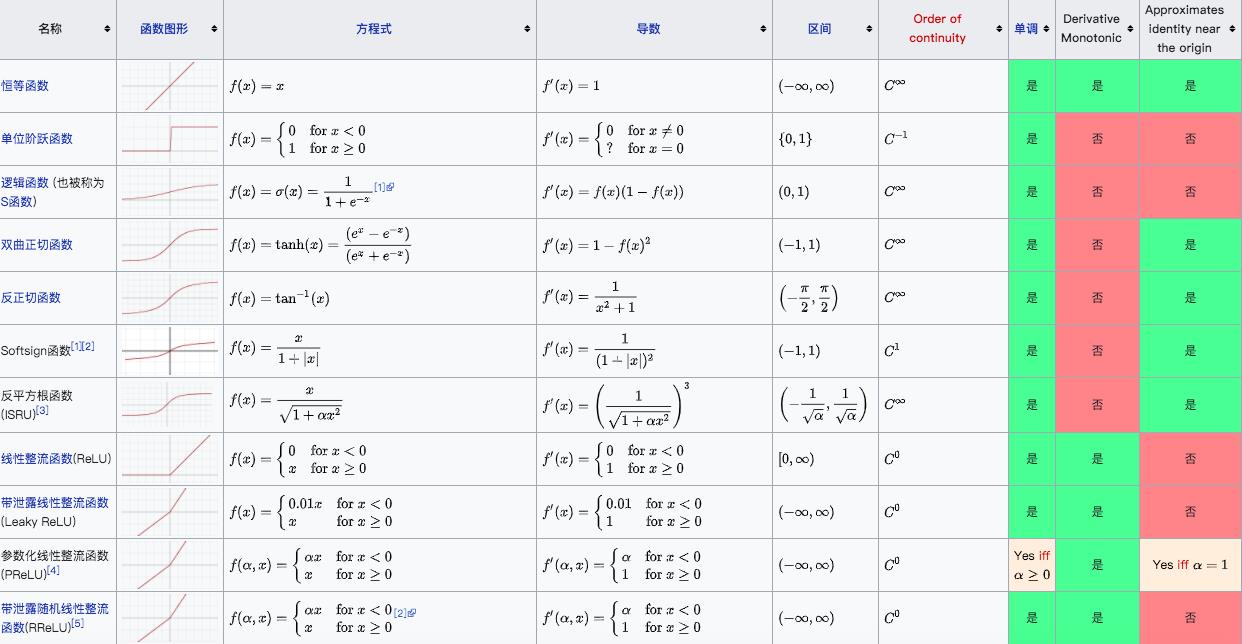
(1)恒等函数

这种激活函数在任意一点处的导数为1.
(2)单位阶跃函数

这种激活函数在任意一点处的导数为0 (除了0点以外)
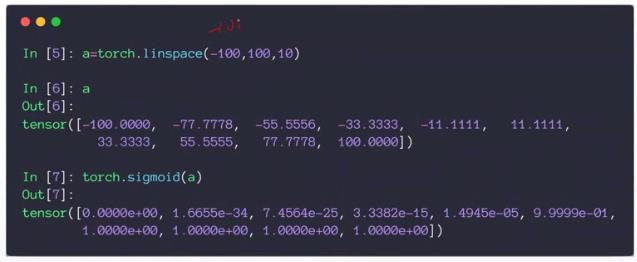
(3)sigmod函数的导数
 可以通过计算某个点X原函数的正向传播值(激活函数),直接得到在某个点处的导数值 = f(x)* (1-(fx))
可以通过计算某个点X原函数的正向传播值(激活函数),直接得到在某个点处的导数值 = f(x)* (1-(fx))
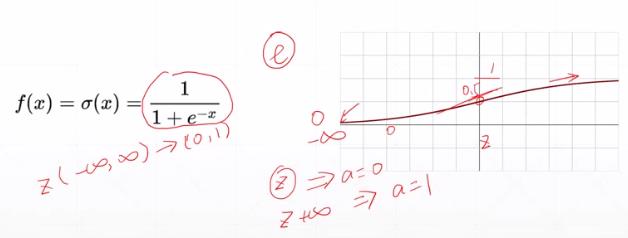
该函数在负无穷和正无穷处的导数接近为0。
该函数在0处的导数最大,为1/2 * 1/2 = 1/4
推导过程如下:
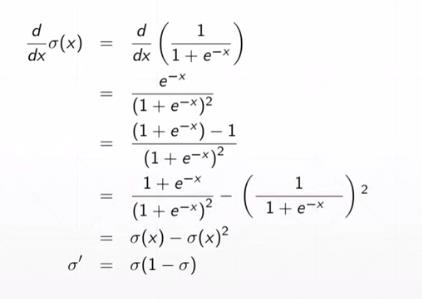
(4)正切函数


可以通过计算某个点X在原函数的正向传播值(激活函数),直接得到在某个点处的导数值 = 1 - f(x)^2,推导过程如下:
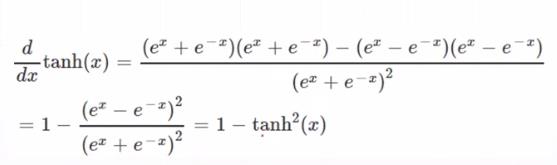
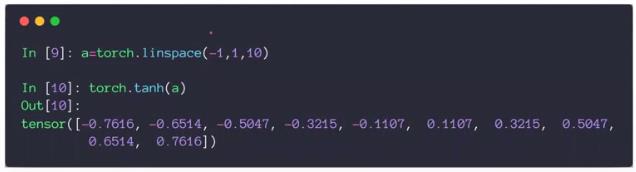
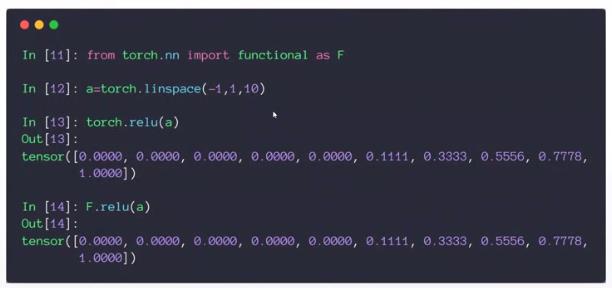
(5)Relu函数的导数


Relu函数都不需要正向传播,只需要检查当前点相对原点的位置:
大于0时,导数为1。
小于0时,导数为0。
3.5 总结:
通过上述案例可以看出,求loss函数在Wi, Bi点处的偏导数,其实比预想的要简单很多。
只需要对loss函数和原预测函数进行正向传播,获取中间值,就可以非常方便的计算出在任意Wi,Bi处的偏导数值,即梯度。
第4章 复合函数的链式求导的原理:通过正向计算的中间值,直接计算, 获得复合函数的梯度。
4.1 常见符合函数的求导规则
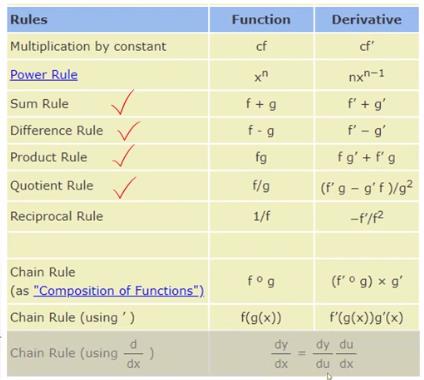
4.2 复合函数的链式求导规则

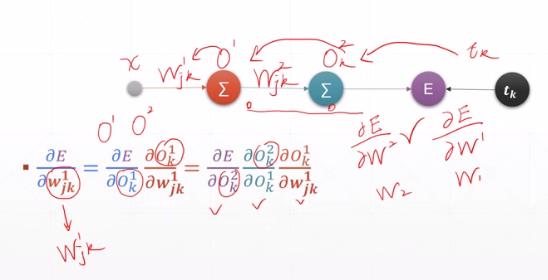
反向链式求导 :每一步都是针对上一级简单函数求偏导,然后把每个步骤中求得的数值进行相乘。
作者主页:文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/120258939
以上是关于[人工智能-深度学习-7]:数据流图正向传播导数梯度梯度下降法反向链式求导,非常非常重要!!!的主要内容,如果未能解决你的问题,请参考以下文章