树状数组的两个操作的证明

Posted 2022-08-23 Harris-H

树状数组的两个操作的证明

首先关于lowbit的证明

我的一篇文章

然后是我画的一张图

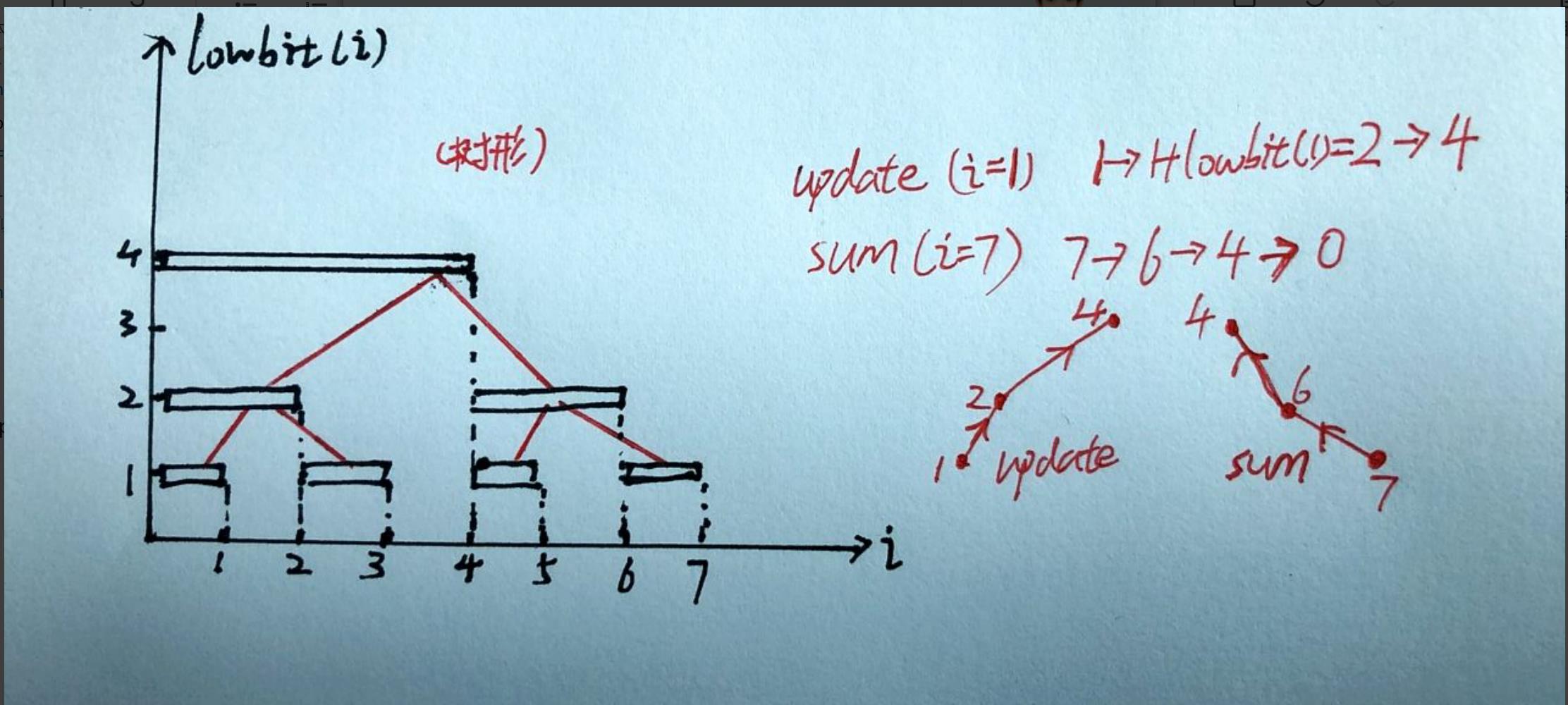
查询操作

当我们要快速求$[1,x]$的前缀和。

可使用lowbit将其划分为多个子区间。

比如当前$x$ 代表的区间为$[x-lowbit(x)+1,x]$ 即长度为$lowbit(x)$的区间。

然后$x^{\prime }=x-lowbit(x)$。

下一段区间就是：$[x^{\prime }-lowbit(x^{\prime })+1,x^{\prime }]$。依此类推最后$x=0$ 结束。

int que(int x)
	int ans=0;
	while(x>0)
		ans+=s[x];
		x-=lowbit(x);
	
	return ans;

更新操作

我们只需证明$x+lowbit(x)$ 所代表的区间一定包含$x$。

这样我们更新就可以保证。

原文传送门

图示

可以发现所有奇数代表的区间长度都是$1$ 即本身。

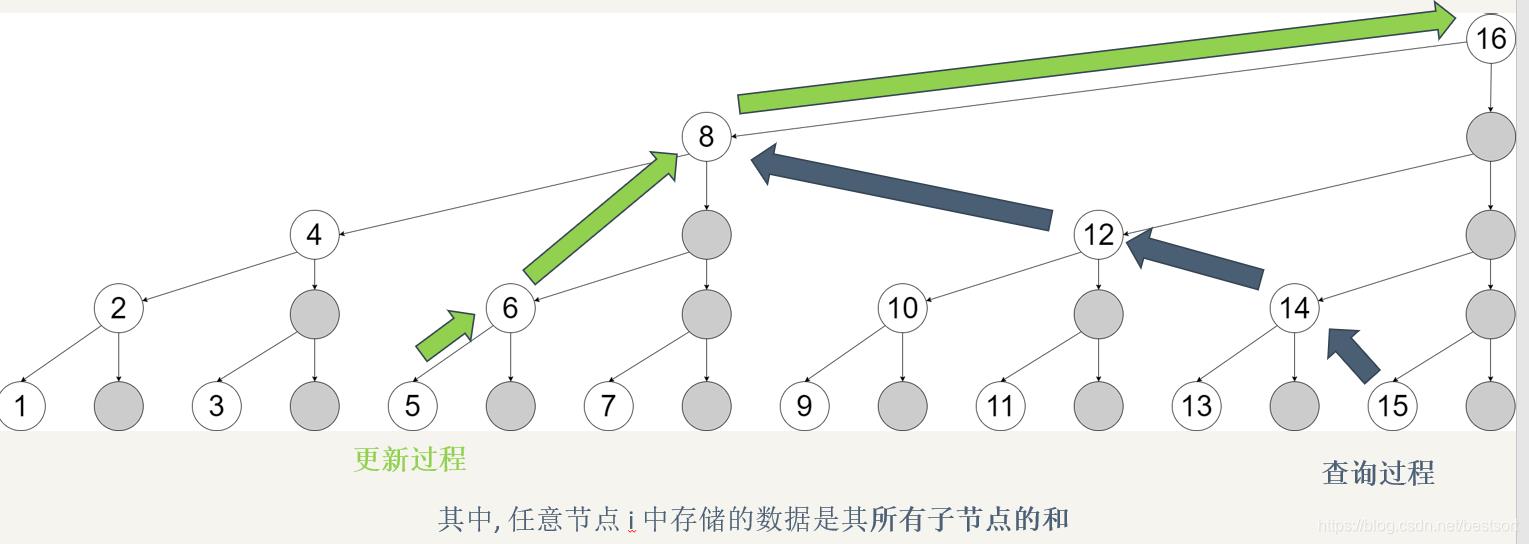
更新类似 树形从子结点到根。方向从下到上，从左到右。

查询类似 树形从子结点到根再到子结点，方向下上下，从右到左。