基于等波纹最佳逼近法的FIR数字滤波器实现matlab仿真

Posted 2022-08-23 fpga和matlab

目录

一、理论基础

二、案例背景

三、MATLAB核心代码

四、仿真结论分析

---

一、理论基础

        等波纹最佳逼近法，其本质是一种优化算法，该方法有效克服了基于窗函数的FIR滤波器设计方法以及基于频率抽样的FIR滤波器设计方法所存在的各种缺点，使得算法的设计误差达到最小值。而基于等波纹最佳逼近法的FIR数字滤波器，其频谱特性曲线在通带和阻带上都具有等纹波特性。

二、案例背景

滤波器的含义，就是指对输入信号有着消除噪声和平滑功能的系统[01]。根据处理信号种类的不同，将处理连续信号的滤波器称为模拟滤波器，将处理离散信号的滤波器称为数字滤波器。随着通信多媒体技术的飞速发展，数字滤波器成为数字信号处理领域中一个越来越重要的组成部分，其广泛应用在信息通信、语音传输、自适应控制等众多领域。从结构上分，数字滤波器可以分为FIR数字滤波器和IIR数字滤波器两种基本类型。其中，FIR滤波器的设计方法有许多种，如窗函数设计法、频率取样法和等波纹最佳逼近法，本文主要针对FIR滤波器的实现原理和设计方法进行了研究。

    数字滤波器本质上讲是一种通过有限精度算法来运算的线性时不变离散系统，其具有特定的传输选择性，数字滤波器的输入和输出信号均为离散数字信号。数字滤波器的工作原理为，通过一个离散数字系统，对输入的数字信号进行运算，处理，变换等各种数字信号操作，从而实现改变数字输入序列的频谱特性或者时域波形，将有用的信号频谱分量进行保留，消除无用的信号频谱分量。数字滤波器，在功能上可以分为低通数字滤波器、高通数字滤波器、带通数字滤波器以及带阻数字滤波器四种类型。相对于模拟滤波器，数字滤波器具有高精度，高稳定性，高灵活性等优势。

三、MATLAB核心代码

clc;
clear;
close all;
 
Wp=0.2*pi; Ws=0.3*pi; wdelta= Ws-Wp;Fs=1000;T=1/Fs;N=1000;
t=0:T:(N-1)*T;
st=sin(2*pi*t*100);
subplot(3,1,1);plot(st);
nt=2*rand(1,N)-1;
xt=nt+st;
subplot(3,1,2);plot(xt);
fp=120;fs=150;Rp=0.2;As=60;Fs=1000;
wc=(fs+fp)/Fs;
B=2*pi*(fs-fp)/Fs;
Nb=ceil(11*pi/B);
hn=fir1(Nb-1,wc,blackman(Nb));
Hw=abs(fft(hn,1024));
ywt=fftfilt(hn,xt,N);
pp=abs(fft(xt,1024));
subplot(3,1,3);
plot(pp);

%用窗函数设计方法绘制滤波器损耗函数以及输出信号波形
hd = dfilt.dffir(hn)
[H,W]=freqz(hd);
m=abs(H);
figure(2);subplot(3,1,1);
plot(W/pi,20*log10(m/max(m)));grid on;
xlabel('\\omega/\\pi');ylabel('幅度(dB)')
axis([0,1,-100,0]);title('损耗函数曲线及其频谱图')
subplot(3,1,2);
plot(ywt);
ss=abs(fft(ywt,1024));
subplot(3,1,3);
plot(ss);


%用等波纹最佳逼近法设计滤波器
fb=[fp,fs];m=[1,0];
dev=[(10^(Rp/20)-1)/(10^(Rp/20)+1),10^(-As/20)];
[Ne,fo,mo,W]=remezord(fb,m,dev,Fs);
hn=remez(Ne,fo,mo,W);
Hw=abs(fft(hn,1024));
yet=fftfilt(hn,xt,N);

%用等波纹最佳逼近方法绘制滤波器损耗函数以及输出信号波形
hd = dfilt.dffir(hn)
[H,W]=freqz(hd);
m=abs(H);
figure(3);subplot(3,1,1);
plot(W/pi,20*log10(m/max(m)));grid on;
xlabel('\\omega/\\pi');ylabel('幅度(dB)')
axis([0,1,-100,0]);title('损耗函数曲线及其频谱图')
subplot(3,1,2);
plot(yet);
aa=abs(fft(yet,1024));
subplot(3,1,3);
plot(aa);


figure;
plot(W/pi,20*log10(m/max(m)));grid on;
xlabel('\\omega/\\pi');ylabel('幅度(dB)')
axis([0,1,-100,0]);

clc;
clear;
close all;
 
Wp=0.15*pi; Ws=0.4*pi; wdelta= Ws-Wp;Fs=1000;T=1/Fs;N=1000;
t=0:T:(N-1)*T;
st=sin(2*pi*t*100);
% subplot(3,1,1);plot(st);
nt=2*rand(1,N)-1;
xt=nt+st;
% subplot(3,1,2);plot(xt);
fp=120;fs=150;Rp=0.2;As=60;Fs=1000;
wc=(fs+fp)/Fs;
B=2*pi*(fs-fp)/Fs;
Nb=ceil(11*pi/B);
hn=fir1(Nb-1,wc,blackman(Nb));
Hw=abs(fft(hn,1024));
ywt=fftfilt(hn,xt,N);
pp=abs(fft(xt,1024));
% subplot(3,1,3);
% plot(pp);

%用窗函数设计方法绘制滤波器损耗函数以及输出信号波形
hd = dfilt.dffir(hn)
[H,W]=freqz(hd);
m=abs(H);
 

%用等波纹最佳逼近法设计滤波器
fb=[fp,fs];m=[1,0];
dev=[(10^(Rp/20)-1)/(10^(Rp/20)+1),10^(-As/20)];
[Ne,fo,mo,W]=remezord(fb,m,dev,Fs);
hn=remez(Ne,fo,mo,W);
Hw=abs(fft(hn,1024));
yet=fftfilt(hn,xt,N);

%用等波纹最佳逼近方法绘制滤波器损耗函数以及输出信号波形
hd = dfilt.dffir(hn)
[H,W]=freqz(hd);
m=abs(H);
figure;
subplot(3,1,1);
plot(W/pi,20*log10(m/max(m)));grid on;
xlabel('\\omega/\\pi');ylabel('幅度(dB)')
axis([0,1,-100,0]);title('损耗函数曲线及其频谱图')
subplot(3,1,2);
plot(yet);
aa=abs(fft(yet,1024));
subplot(3,1,3);
plot(aa);


figure;
plot(W/pi,20*log10(m/max(m)));grid on;
xlabel('\\omega/\\pi');ylabel('幅度(dB)')
axis([0,1,-100,0]);

freqz(hn,1,512); 

Ts=1/1000  ;%设置采样频率
t=0:Ts:3*pi;
y=sin(2*pi*t)+cos(400*pi*t)+cos(600*pi*t);

y_Win=filter(hn,1,y);
figure
plotspec(y_Win,Ts); 

figure
plotspec(y,Ts); 

四、仿真结论分析

    利用MATLAB可以响应的低通滤波器的时域和频率的波形图：

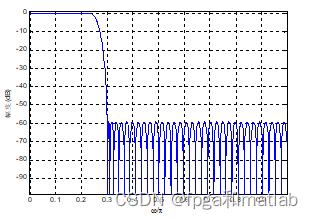
       等波纹最佳逼近法的最优逼近，是指在滤波器长度已知的情况下，通过加权优化的方法，使得纹波误差的值达到最小。因此，在相同阶数的情况下，基于等波纹最佳逼近法的FIR数字滤波器的通带衰减最小，阻带衰减最大。而在相同性能的情况下，基于等波纹最佳逼近法的FIR数字滤波器的阶数可以达到最小。

    这里对等波纹逼近法所设计的FIR滤波器进行仿真，通过MATLAB仿真，获得如下的仿真结果：

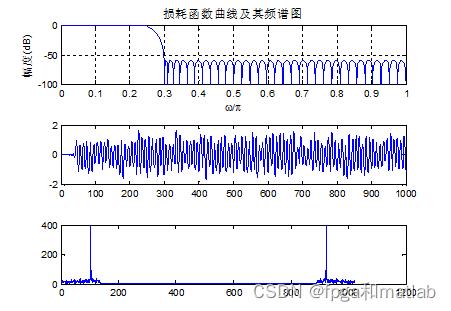
     从图的仿真结果克制，当信号中存在较大干扰噪声的时候，通过等波纹逼近法所设计的FIR滤波器依旧可以获得较好的滤波效果。A25-25