推荐系统DeepFM模型(A Factorization-Machine based Neural Network)
Posted 天泽28
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了推荐系统DeepFM模型(A Factorization-Machine based Neural Network)相关的知识,希望对你有一定的参考价值。
推荐系统(十)DeepFM模型(A Factorization-Machine based Neural Network)
推荐系统系列博客:
- 推荐系统(一)推荐系统整体概览
- 推荐系统(二)GBDT+LR模型
- 推荐系统(三)Factorization Machines(FM)
- 推荐系统(四)Field-aware Factorization Machines(FFM)
- 推荐系统(五)wide&deep
- 推荐系统(六)Deep & Cross Network(DCN)
- 推荐系统(七)xDeepFM模型
- 推荐系统(八)FNN模型(FM+MLP=FNN)
- 推荐系统(九)PNN模型(Product-based Neural Networks)
DeepFM是哈工大和华为合作发表在IJCAI2017上的文章,这篇文章也是受到谷歌wide&deep模型的启发,是一个左右组合(混合)模型结构,不同的是,在wide部分用了FM模型来代替LR模型。因此,强烈建议在看这篇文章之前,先移步看完我之前写的关于wide&deep的博客: 推荐系统(五)wide&deep。我们来看看DeepFM相比较wide&deep模型的改进点及优势(前提是你已经很了解wide&deep模型了):
- 在wide部分使用FM代替了wide&deep中的LR,有了FM自动构造学习二阶(考虑到时间复杂度原因,通常都是二阶)交叉特征的能力,因此不再需要特征工程。Wide&Deep模型中LR部分依然需要人工的特征交叉,比如【用户已安装的app】与【给用户曝光的app】两个特征做交叉。另外,仅仅通过人工的手动交叉,又回到了之前在讲FM模型中提到的,比如要两个特征共现,否则无法训练。
- 在DeepFM模型中,FM模型与DNN模型共享底层embedding向量,然后联合训练。这种方式也更符合现在推荐/广告领域里多任务模型多塔共享底座embedding的方式,然后end-to-end训练得到的embedding向量也更加准确。
其实如果你很熟悉wide&deep模型,再经过上面的介绍,你基本已经知道DeepFM的大体网络结构了。接下来,本文将从两个方面介绍deepFM:
- DeepFM的模型结构细节
- DeepFM的代码实现
- 总结
一、DeepFM的模型结构细节
来看下DeepFM的模型结构(图片来自王喆《深度学习推荐系统》,ps:原论文的图不清晰,所以没有直接从原论文取图)
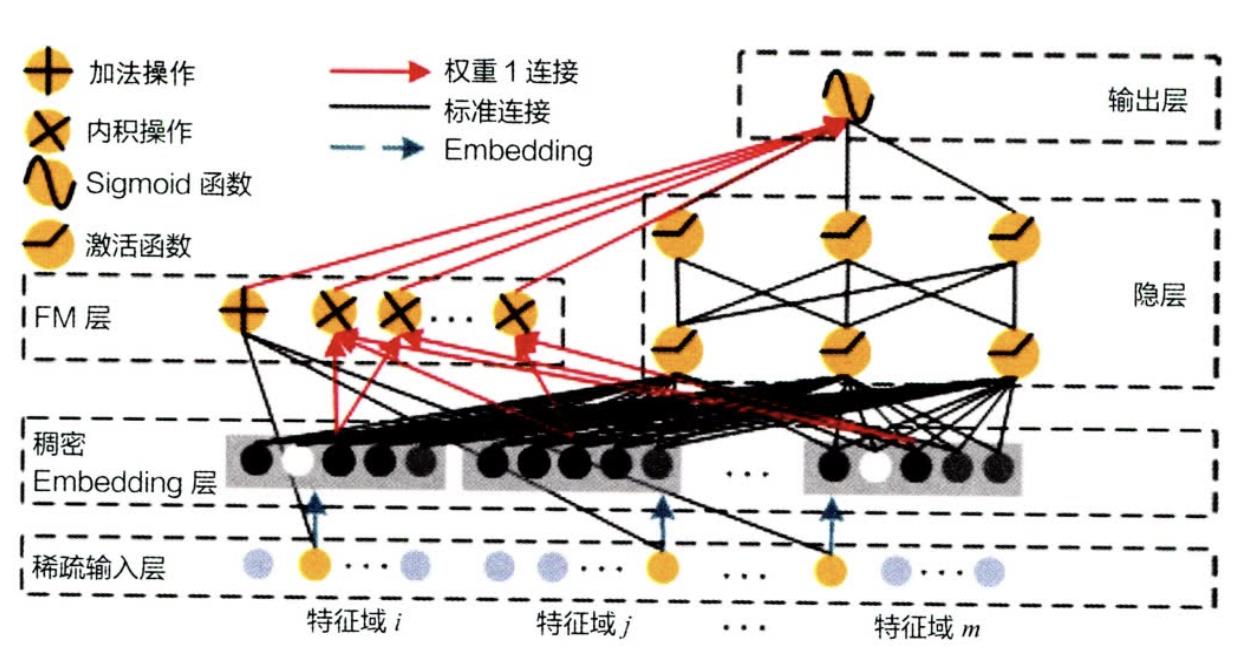
整体模型结构也比较简单,自底向上看分别为:
- 原始输入层:onehot编码的稀疏输入
- embedding层:FM和DNN共享的底座
- FM与DNN
- 输出层
1.1 FM
重点说下FM层,先来回顾下FM的公式:
y
^
(
x
)
=
w
0
+
∑
i
=
1
n
w
i
x
i
+
∑
i
=
1
n
∑
j
=
i
+
1
n
<
v
i
,
v
j
>
x
i
x
j
(1)
\\haty(x) = w_0 + \\sum_i=1^nw_ix_i + \\sum_i=1^n\\sum_j=i+1^n<v_i, v_j>x_ix_j \\tag1
y^(x)=w0+i=1∑nwixi+i=1∑nj=i+1∑n<vi,vj>xixj(1)
上面的公式分为两个部分:
1.1.1 一阶部分
w 0 + ∑ i = 1 n w i x i (2) w_0 + \\sum_i=1^nw_ix_i \\tag2 w0+i=1∑nwixi(2)
其实就是个LR,没什么要说的。
1.1.2 二阶部分
∑ i = 1 n ∑ j = i + 1 n < v i , v j > x i x j (3) \\sum_i=1^n\\sum_j=i+1^n<v_i, v_j>x_ix_j \\tag3 i=1∑nj=i+1∑n<vi,vj>xixj(3)
在讲解 推荐系统(三)Factorization Machines(FM)的博客里讲过,公式(3)直接算(两两交叉算内积)时间复杂度为
O
(
N
2
)
O(N^2)
O(N2),FM论文中给出了推导,把时间复杂度降低至
O
(
K
N
)
O(KN)
O(KN):
∑
i
=
1
n
∑
j
=
i
+
1
n
<
v
i
,
v
j
>
x
i
x
j
=
1
2
[
∑
i
=
1
n
∑
j
=
1
n
<
v
i
,
v
j
>
x
i
x
j
−
∑
i
=
1
n
<
v
i
,
v
i
>
x
i
x
i
]
=
1
2
(
∑
i
=
1
n
∑
j
=
1
n
∑
f
=
1
k
v
i
,
f
⋅
v
j
,
f
x
i
x
j
−
∑
i
=
1
n
∑
f
=
1
k
v
i
,
f
⋅
v
i
,
f
x
i
x
i
)
=
1
2
∑
f
=
1
k
(
(
∑
i
=
1
n
v
i
,
f
x
i
)
(
∑
j
=
1
n
v
j
,
f
x
j
)
−
∑
i
=
1
n
v
i
,
f
2
x
i
2
)
=
1
2
∑
f
=
1
k
(
(
∑
i
=
1
n
v
i
,
f
x
i
)
2
−
∑
i
=
1
n
v
i
,
f
2
x
i
2
)
(4)
\\beginaligned & \\sum_i=1^n\\sum_j=i+1^n<v_i, v_j>x_ix_j \\\\ &= \\frac12 \\tag 4[\\sum_i=1^n\\sum_j=1^n<v_i, v_j>x_ix_j - \\sum_i=1^n<v_i, v_i>x_ix_i] \\\\ &= \\frac12(\\sum_i=1^n\\sum_j=1^n\\sum_f=1^kv_i,f \\cdot v_j,f x_ix_j - \\sum_i=1^n\\sum_f=1^kv_i,f \\cdot v_i,f x_ix_i) \\\\ &=\\frac12\\sum_f=1^k((\\sum_i=1^nv_i,fx_i)(\\sum_j=1^nv_j,fx_j) - \\sum_i=1^nv_i,f^2x_i^2) \\\\ &=\\frac12\\sum_f=1^k((\\sum_i=1^n v_i,fx_i)^2 -\\sum_i=1^nv_i,f^2x_i^2) \\endaligned
i=1∑nj=i+1∑n<vi,vj>xixj=21[i=1∑nj=1∑n<vi,vj>xixj−i=1∑n<vi,vi>xixi]=21(i=1