推荐系统FM系列文章-- AFM模型

Posted 2021-05-01 机器学习BOX

0. 写在前面

前面我们介绍了FM系列的三大模型，包括FM模型，DeepFM以及NFM。DeepFM与NFM模型都对FM做了不同程度的优化，重点都是结合神经网络实现对特征的高阶组合。今天我们来介绍将attention机制应用于FM模型的AFM模型（Attentional Factorization Machine）。

个人心得：

1. 特征组合的重要性会随预测目标的改变而发生变化
2. attention机制用于学习特征交叉前的不同权重

https://www.ijcai.org/Proceedings/2017/0435.pdf

1. 背景

对于传统的FM模型以及DeepFM、NFM模型，二阶交叉项中特征向量的系数均为1，然而，在某些推荐场景下，不同的二阶交叉特征对预测当前目标的权重是不同的。为了让模型能够学习不同二级交叉特征项的权重，AFM引入了Attention机制。

实际上，AFM仍然分为shallow-part和dnn-part，shallow-part与其他模型相同，这里就不重复说明了。下面，我们将从整体模型架构，pair-wise interation layer, Attention layer三部分对AFM模型的dnn部分进行介绍。

2. 整体架构

AFM模型架构如图所示。模型整体包含五部分，分别为稀疏特征输入、embedding layer、pair-wise interaction layer、attention-based pooling layer, predict layer. 其中，输入层接受稀疏特征传入，经embedding后，得到每个特征域的embedding特征向量，向量维度均保持一致。

前两步是FM系列神经网络推荐模型的常规操作，没有做任何特殊处理。每个embedding特征向量会经过一层pair-wise interaction layer,进行特征向量两两交叉的操作，获得二阶特征项。同时，将每个二阶特征向量送入Attention layer，输出该特征向量的权重值，并通过sum-pooling加权得到一个综合所有特征信息的向量，然后经过全连接层输出预测结果。

3. pair-wise interaction layer

我们先来看看这一层的实现方式，其数学表达式如下式所示。

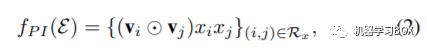
其中， 表示特征域对应的embedding向量， 表示特征取值， 表示element-wise product操作。这样一看，是不是和NFM中的bi-interaction很类似呢。pair-wise interaction layer通过将特征embedding向量进行两两交叉，得到二阶特征项。同时，二阶特征项个数为 ，其中 为样本特征域个数。

4. attention-based pooling layer

既然设计者将模型称之为attention-fm，那么attention机制的引入一定是论文最大的亮点。下面我们一起来看下AFM中的attention-based pooling layer是如何设计及实现的。

为了能够估计二阶向量的权重，一个比较直接的方法就是通过最小化loss函数去学习其值，虽然看起来是可行的，但是这又会碰到之前的问题：当某个交互特征没有出现在样本中时，就无法计算得到某个交互特征的attention分数了。为了解决这个泛化能力方面的问题，AFM使用MLP网络去参数化这个attention分数，该MLP网络称之为attention layer。Attention layer的数学表达式如下所示。

可以看出，attention layer的输入为每一个二阶特征向量，经过一层MLP后，送入softmax归一化为每个二阶特征向量的权重。其中，网络的激活函数使用的是常用的ReLU，隐层神经元个数作为attention layer的超参数，需要经网络调优得到。得到每个二阶特征向量的权重后，AFM通过对所有二级特征向量进行加权sum-pooling的方式，得到综合所有特征信息的向量，并送入全连接层，经softmax得到最终预测结果。

5. 总结

AFM在FM模型的基础上，引入了attention机制，使模型能够有效学习二阶特征项的权重，这是DeepFM、NFM等模型均未能考虑到的。