机器学习实验五基于多分类线性SVM实现简易人机猜拳游戏
Posted helton_yann
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习实验五基于多分类线性SVM实现简易人机猜拳游戏相关的知识,希望对你有一定的参考价值。
文章目录
基于多分类线性SVM&mediapipe手势关键点实现简易人机猜拳游戏
在【机器学习算法】支持向量机入门教程及相关数学推导 这篇博客中,我们已经完整的推导了SVM算法以及SMO序列最小化优化算法的来龙去脉。在本篇博客中,我们将基于这些理论基础,手写代码实现SVM算法的完整实现过程。并基于分类结果进行数据+决策面的可视化;同时,填一下上上上上上篇博客挖的坑,实现一个有趣的小应用:上次是基于逻辑斯蒂回归,这次我们用SVM算法来进行手势识别。
本次实验的所有代码已上传至github:https://github.com/Scienthusiasts/Machine-Learning
先贴一张实现效果:

基于SMO优化的SVM分类算法完整实现版本
本次手写代码的主要理论基础在【机器学习算法】支持向量机入门教程及相关数学推导中都有比较详尽的解释,推荐这两篇博客可以对照着看,相信对大家一定会有不一样的体会与理解。🎈
首先,我们构造一个类来实现SVM算法,类中包括算法的超参数,待优化的模型参数,以及模型用到的训练样本等:
class SVM:
def __init__(self, X, y, C, ε, ker):
self.X = X # 数据集
self.y = y # 标签
self.C = C # 松弛变量在损失中的权重
self.ε = ε # 容忍一定的误差
self.m = X.shape[0] # X总数
self.α = np.zeros((self.m, 1)) # 待求解参数α
self.b = 0 # 待求解参数b
self.ker = ker # 核函数参数
# eCache存储每个参数的误差E,第一列为是否有效的标志位(是否计算过而不是初始的0)
self.eCache = np.zeros((self.m, 2))
然后,SVM一个必不可少的通过样本的高维映射实现非线性划分的方法就是引入核函数。
核函数的种类有许多,在本例中我们采用最简单和常用的两种:线性核和高斯核
# 核函数
def K(self, xi, xj, param=0):
# 线性核函数
if param == 0:
xj = xj.reshape(-1, 1)
return np.dot(xi, xj)
# 高斯核函数
if param == 1:
σ = 1.3 # 核函数的方差σ是一个超参数
deltaRow = xi - xj
ker = np.exp(-np.dot(deltaRow, deltaRow.T) / (2 * σ * σ))
return ker
在SMO优化过程中,为了更新后的α2能用更新前的α2表示,而不是不够直观的ζ,我们需要用到标签与模型预测结果之间的差值E。同时,启发式搜索αj也需要用到E。
因此我们需要定义一个方法来实现对E的求解:
# 计算误差Ek
def calcEk(self, k):
# 计算SVM模型的预测结果:
fk = np.sum([self.α[i] * self.y[i] * self.K(self.X[i,:], self.X[k,:], self.ker) for i in range(self.m)]) + self.b
# 计算误差:
Ek = fk.reshape(1) - self.y[k]
return Ek
由于我们定义了一个误差缓存eCache来记录这些误差,因此顺便实现一个误差更新方法:
# 更新第k个参数的误差
def updateEk(self, k):
# 计算误差
Ek = self.calcEk(k)
# 更新计算后的误差
self.eCache[k,0] = 1
self.eCache[k,1] = Ek
在SMO选取参数αj的过程中,使用的是基于误差E最小的启发式的方法,这里定义一个方法实现:
# 随机选取第二个参数, 不同于i即可
def selectJRand(self, i, m):
j = i
while(j==i):
j = int(random.uniform(0, m))
return j
# 启发式选取第j个参数, 更高效
def selectJ(self, i, Ei):
bestJ = -1 # 最佳误差对应第几个α
maxDeltaE = 0 # 记录最大误差|Ei - Ej|
Ej = 0 # 记录最佳参数αj对应的误差Ej
# 获取那些已经更新过的Ek(非0)
validE = np.nonzero(self.eCache[0,:])[0]
if len(validE) > 1:
# 遍历那些已经计算过的Ei,选择其中最大的对于的αj作为第二个参数
for k in validE:
# j和i不能是同一个
if k == i: continue
# 计算当前alpha的E
Ek = self.calcEk(k)
# 两个差值要最大
deltaE = abs(Ei - Ek)
if deltaE > maxDeltaE:
bestJ = k
maxDeltaE = deltaE
Ej = Ek
return bestJ, Ej
else: # 对于第一次更新的情况,Ek还没更新过
j = self.selectJRand(i, self.m)
Ej = self.calcEk(j)
return j, Ej
在SMO求得αj的值后,由于约束条件的存在,我们还需要对违背约束条件的αj进行截断:
# 根据约束条件约束求得的α(矩形+线性区域)
def clipAlpha(self, αj, H, L):
if αj > H:
αj = H
if αj < L:
αj = L
return αj
在定义了一些零零碎碎但是必不可少的方法后,接下来就是对基于一次迭代的SMO优化算法流程的完整实现(更新一对参数):
# SMO优化算法流程:
def innerL(self, i):
# 计算误差
Ei = self.calcEk(i)
# K.K.T.条件 (ε是一个很小的数,容忍一些误差?)
# (1) αi = 0 => yi(wTxi + b) - 1 > 0 + ε 【非支持向量】
# (2) 0 < αi < C => yi(wTxi + b) - 1 = 0 【支持向量】
# (3) αi = C => yi(wTxi + b) - 1 ≤ 0 - ε 【内嵌向量】
# 启发式寻找参数i(如果满足K.K.T.条件直接跳过):
# if语句用来判断是否违法了K.K.T.条件(3)(1):
if ((self.y[i]*Ei < -self.ε) and (self.α[i] < self.C)) or ((self.y[i]*Ei > self.ε) and (self.α[i] > 0)):
# 启发式寻找参数j:
j, Ej = self.selectJ(i, Ei)
old_αi, old_αj = self.α[i].copy(), self.α[j].copy()
# 先求好这三个参数,之后会用到
K11 = self.K(self.X[i,:], self.X[i,:], self.ker)
K12 = self.K(self.X[i,:], self.X[j,:], self.ker)
K22 = self.K(self.X[j,:], self.X[j,:], self.ker)
# αi 和 αj 的解带有约束:
# (1) αiyi + αjyj = ζ
# (2) 0 < αi,j < C
# 分情况求解待约束的解:
if self.y[i] != self.y[j]:
L = max(0, self.α[j] - self.α[i])
H = min(self.C, self.C + self.α[j] - self.α[i])
else:
L = max(0, self.α[j] + self.α[i] - self.C)
H = min(self.C, self.α[j] + self.α[i])
# 打印一些优化时的参数信息
# L == H的情况是αj正好在矩形约束对角线的点上
# 若 L = H,αj = L = H
if(L == H): print("出现 L = H = %f, i = %d, j = %d, αj=%f" %(L, i, j, self.α[j])); return 0
η = -2.0 * K12 + K11 + K22
# 若 η <= 0,就无需优化了???
if η <= 0: print("η <= 0"); return 0
# 若 η >= 0,有更新公式:
self.α[j] += self.y[j] * (Ei - Ej) / η
# 约束α的范围
self.α[j] = self.clipAlpha(self.α[j], H, L)
# 更新αj的误差
self.updateEk(j)
if(np.abs(self.α[j] - old_αj) < 1e-5):
print("j 更新的太少")
return 0
# 更新αi
self.α[i] += self.y[i] * self.y[j] * (old_αj - self.α[j])
# 接下来求解参数b:
D_αi, D_αj = (self.α[i] - old_αi), (self.α[j] - old_αj)
b1 = - Ei - self.y[i] * K11 * D_αi - self.y[j] * K12 * D_αj + self.b
b2 = - Ej - self.y[i] * K12 * D_αi - self.y[j] * K22 * D_αj + self.b
# 分情况更新参数b:
if 0 < self.α[i] < self.C: self.b = b1
elif 0 < self.α[j] < self.C: self.b = b2
else: self.b = (b1 + b2) / 2.0
return 1
else: return 0
启发式的寻找αi,将innerL(self, i)写在迭代流中,并实时输出迭代更新的参数信息;模型收敛或达到最大迭代次数后退出。我们将这一过程封装成训练方法:
# 训练流程,基于SMO算法
def train(self, maxIter):
iter = 0 # 记录迭代次数
entireSet = True
αPairsChanged = 0
# 当迭代次数超过最大迭代次数或任何α都无需优化时(收敛), 退出
while(iter < maxIter) and ((αPairsChanged > 0) or (entireSet)):
αPairsChanged = 0
if entireSet:
print("===========================全数据集遍历===========================")
# 遍历针对所有向量
for i in range(self.m):
# 选取αij并更新
αPairsChanged += self.innerL(i)
print("Iteration:%d | choosed i=%d | 已更新的参数对数:%d" % (iter, i, αPairsChanged))
iter += 1
# print("已优化所有参数,算法提前结束!")
# break
else:
print("===========================非边界值遍历===========================")
# 仅遍历非边界向量
nonBoundIs = np.nonzero((self.α>0) * (self.α<self.C))[0]
# 遍历非边界值
for i in nonBoundIs:
αPairsChanged += self.innerL(i)
print("Iteration:%d | choosed i=%d | 已更新的参数对数:%d" % (iter, i, αPairsChanged))
iter += 1
# 遍历一次后改为非边界遍历
if entireSet:
entireSet = False
# 如果alpha没有更新,计算全样本遍历
elif (αPairsChanged == 0):
entireSet = True
if(iter >= maxIter):print("超过最大迭代次数,算法结束")
if not((αPairsChanged < 0) or (entireSet)):print("算法收敛")
# 对于线性核:
if(self.ker == 0):
self.W = np.zeros((self.X.shape[1], 1))
for i in range(self.m):
self.W += self.α[i] * self.y[i] * self.X[i,:].reshape(-1,1)
return self.W, self.b
# 对于非线性核:
return self.b, self.α
在模型训练完毕后,可以保存模型权重以便离线使用:
值得注意的是,能够使用参数W和b的模型仅限于线性SVM(或线性核),对于非线性SVM而言,由于核函数已经将样本X映射到了高维空间,因此我们只能基于参数α,训练集X, b进行模型的推理,而不能基于原始的样本特征。由于训练集X涉及的样本量可能很大,因此本篇博客中我们暂不考虑基于预训练非线性SVM的推理实现。
# 保存权重(线性核)
def save_weight_lin(self, path):
weight = np.concatenate((self.W, self.b.reshape(-1,1)), axis=0)
np.save(path, weight)
同样,模型的预测(评估验证集)也可以分为两种推理方式,基于W和b的线性SVM,基于α,训练集X, b的非线性SVM:
# 测试
# 核心公式就是 y = wTx + b
# 在超平面上方时为y>0,为类别1
# 在超平面下方时为y<0,为类别-1
def eval(self, test_X):
res = []
sv_index = np.nonzero(self.α)[0]
for j in range(test_X.shape[0]):
res.append(self.b + np.sum([self.α[i] * self.y[i] * self.K(self.X[i,:], test_X[j,:], self.ker) for i in sv_index]))
return np.array(res)
# 对于线性核,直接采用y = wTx + b判别方法,避免计算需要使用X(映射到高维空间的核数据不行)
@staticmethod
def linear_eval(test_X, W, b):
res = b + np.dot(test_X, W)
return res
SVM决策结果与数据集可视化
在书《机器学习实战》中,一共提供了两个例子供我们实验。一个好处是,这些数据是二维的,因此我们可以先可视化看看这些数据的分布特征:
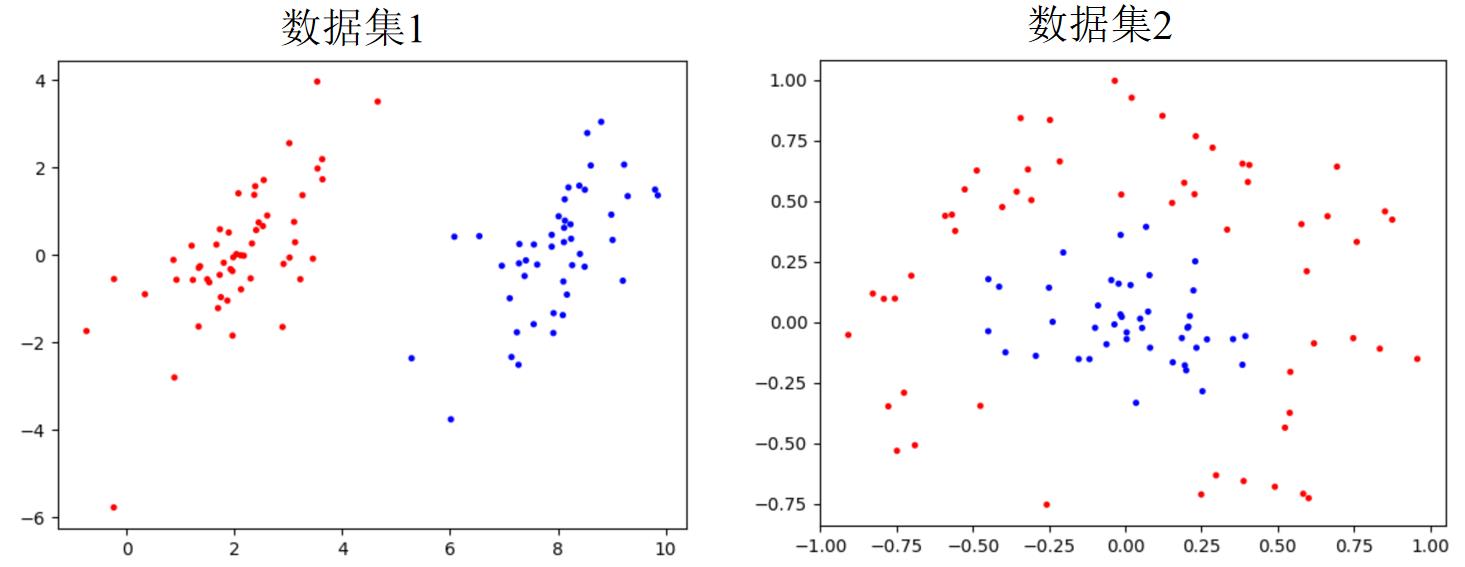
显而易见,数据集1是线性可分的,数据集2是线性不可分的。对于线性可分的数据,采用线性SVM就可以完美的解决问题,对于那些线性不可分的数据,我们需要利用核映射来解决。
测试代码:
if __name__ == '__main__':
kernelType = 0
# 读取数据(txt)
X, y = loadDataSet('./testSet.txt')
y = y.reshape(-1,1)
# visualDataSets2D(X, y)
svm = SVM( X, y, C=0.6, ε=1e-4, ker=kernelType)
_, b, α = svm.train(maxIter=1)
print(α)
# 测试
res = svm.eval(X)
acc = sum(res*y>0) / X.shape[0]
# print("准确率: %f" % (acc))
visualModel2D(X, y, b, α, kernelType)
可视化模型决策结果(数据集1,线性SVM):
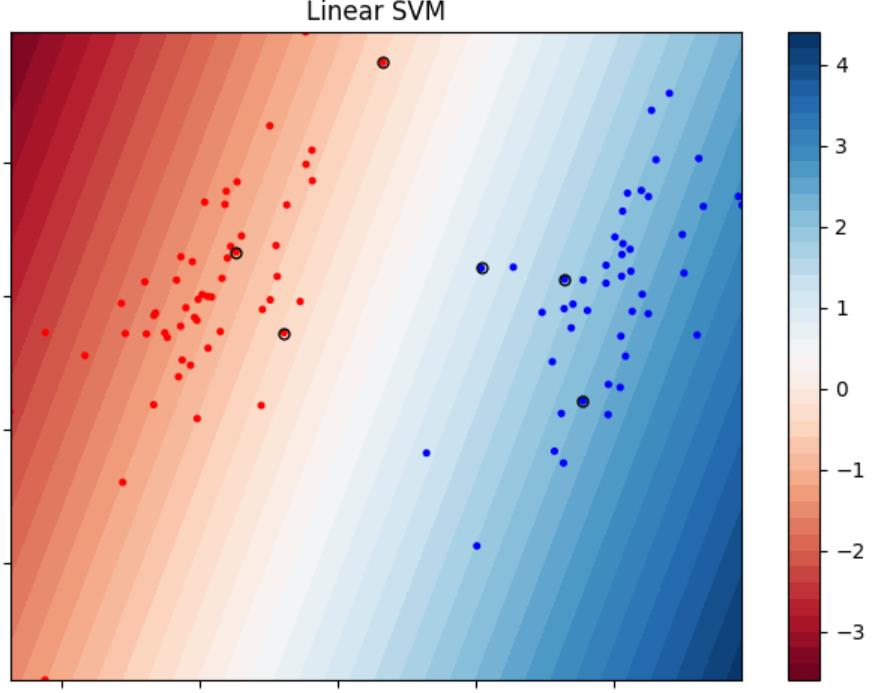
图中圈起来的点代表支持向量,值得注意的是,基于软间隔SVM的支持向量不一定恰好都落在间隔边界上,这是因为软间隔SVM具有一定的容错力,也就是说,最大间隔可能嵌入在样本之中(总之模型肯定会帮助你找到一条最优直线,这条直线是容错率与模型泛化能力的tradeoff)
【但是说实话我还是不太理解为什么线性SVM的支持向量没有恰好在一条直线上,或许是和松弛变量有关。。🐶】
… …
Iteration:0 | choosed i=97 | 已更新的参数对数:4
Iteration:0 | choosed i=98 | 已更新的参数对数:4
Iteration:0 | choosed i=99 | 已更新的参数对数:4
超过最大迭代次数,算法结束
算法收敛
准确率: 1.000000
支持向量个数: 6
对于数据集2而言,可以使用高斯核来引入非线性SVM。
可视化模型决策结果(数据集2,非线性SVM):
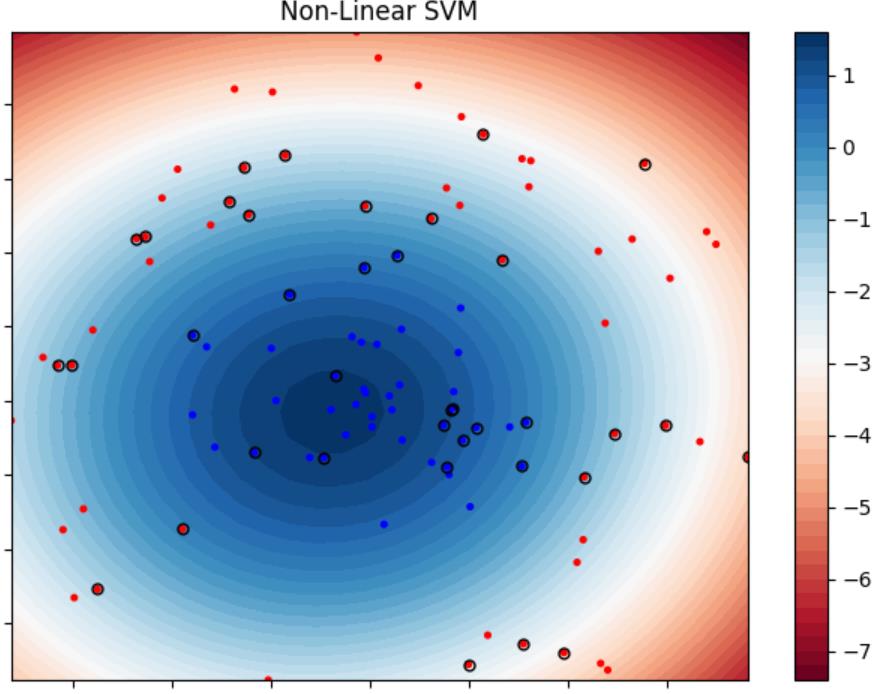
Iteration:0 | choosed i=94 | 已更新的参数对数:26
Iteration:0 | choosed i=97 | 已更新的参数对数:27
Iteration:0 | choosed i=98 | 已更新的参数对数:27
出现 L = H = 0.000000, i = 99, j = 53, αj=0.000000
Iteration:0 | choosed i=99 | 已更新的参数对数:27
超过最大迭代次数,算法结束
算法收敛
准确率: 0.990000
支持向量个数: 37
一般而言,对于线性可分的数据,在其任意高维的某个特征空间中都一定是线性可分的,因此我们可以对数据集1引入高斯核:
可视化模型决策结果(数据集1,非线性SVM):
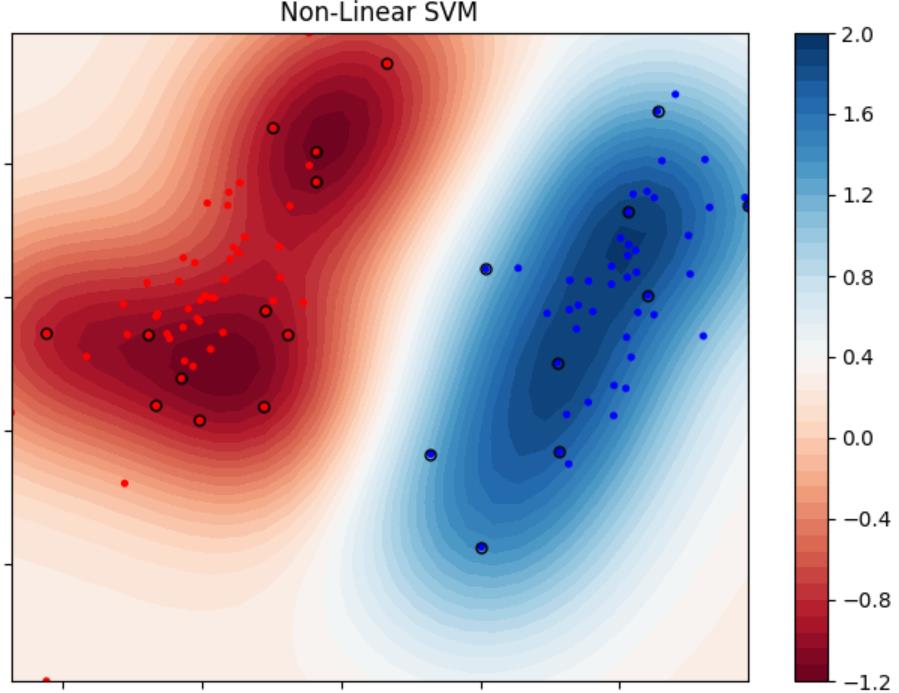
Iteration:0 | choosed i=98 | 已更新的参数对数:15
出现 L = H = 0.000000, i = 99, j = 85, αj=0.000000
Iteration:0 | choosed i=99 | 已更新的参数对数:15
超过最大迭代次数,算法结束
算法收敛
准确率: 0.990000
支持向量个数: 21
多分类SVM实战:基于mediapipe手势关键点实现简易版人机猜拳
在上一节机器学习实战中,我们利用逻辑斯蒂回归算法实现了二分类手势识别。在本节中,我们将核心算法改为线性SVM,实现手势三分类。具体的数据采集方法以及如何使用mediapipe工具包在上一次博客中已经有了详细的说明,感兴趣的小伙伴可以点击传送门:【机器学习实验四】基于Logistic Regression二分类算法实现手部姿态识别
二分类算法如何实现多分类
SVM和逻辑斯蒂回归算法有一个相同点,那就是它们都只能执行二分类任务,要实现对于两个以上类别的多分类,我们可以采取一些特殊的方法:
1. OVO(one versus one)
ovo即一对一的方法,我们可以将多个类别两两组合,假设有n个类别,两两组合就能产生n(n-1)/2个数据集,这时候我们需要对每对组合的数据集训练一个模型,总共训练n(n-1)/2个模型。在每次预测时,采用投票的方式选择预测类别最多的那个类别作为最终的预测结果。
基于ovo训练方法的缺点在于,一旦数据类别一多,需要训练的模型的个数将以平方级别增长,因此这种方法适用于小类别下的简单数据集。
下面这张图很直观的表达了ovo数据集划分方法:
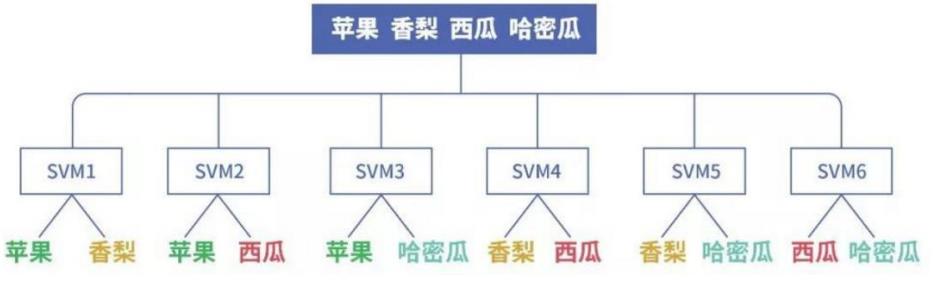
2.OVR(one versus rest)
ovr即一对多方法,在数据划分时依次将某个类别的样本归为正例而其余的样本归为负例。假设有n个类别,我们就需要训练n个模型。在每次预测时,选择唯一分为正例的模型对应的类别作为最终预测结果。如果同时有多个模型预测出正例,则选取期望值最大的那个(对于SVM就是数值>0且越大越好)
基于ovr训练方法的缺点也比较明显,那就是正负例的样本很有可能分布不均衡,负例的样本数通常比较大。
下面这张图很直观的表达了ovr数据集划分方法:
 机器学习SVM多分类问题及基于sklearn的Python代码实现
机器学习SVM多分类问题及基于sklearn的Python代码实现