旋转矩阵与欧拉角之间的转换
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了旋转矩阵与欧拉角之间的转换相关的知识,希望对你有一定的参考价值。

简 介: 对于欧拉角与旋转矩阵之间的转换公式和程序实现进行了测试。也显示了这其中的转换关系的复杂性,来自于欧拉角的方向、范围、转换顺序。这在实际应用中需要特别的关注。
关键词: 欧拉角,旋转矩阵
在机器人视觉应用中,经常会遇到旋转矩阵、旋转向量、四元素、欧拉角之间的相互转换。其中最容易出错的是旋转矩阵与欧拉角之间的相互转换。
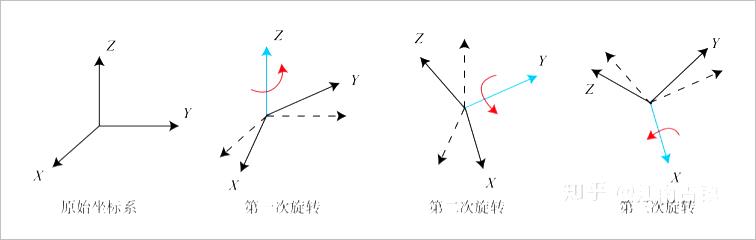
▲ 图1 坐标系旋转变换
§01 欧拉角
1.1 基本概念
1.1.1 欧拉角的名称
- 欧拉角的叫法不固定,跟坐标轴的定义强相关。
- 在图1中,假设X是车头,Y是车左方,Z是车上方,那么绕X轴旋转得到的是roll,绕Y轴旋转得到的是pitch,绕Z轴得到的是yaw。
- 在图1中,假设Y是车头,X是车右方,Z是车上方,那么绕X轴旋转得到的是pitch,绕Y轴旋转得到的是roll,绕Z轴得到的是yaw。
1.1.2 欧拉角方向
- 如果是右手系,旋转轴正方向面对观察者时,逆时针方向的旋转是正、顺时针方向的旋转是负。
- 亦可这样描述:使用右手的大拇指指向旋转轴正方向,其他4个手指在握拳过程中的指向便是正方向。
- 如图1中的三次旋转都是正向旋转。
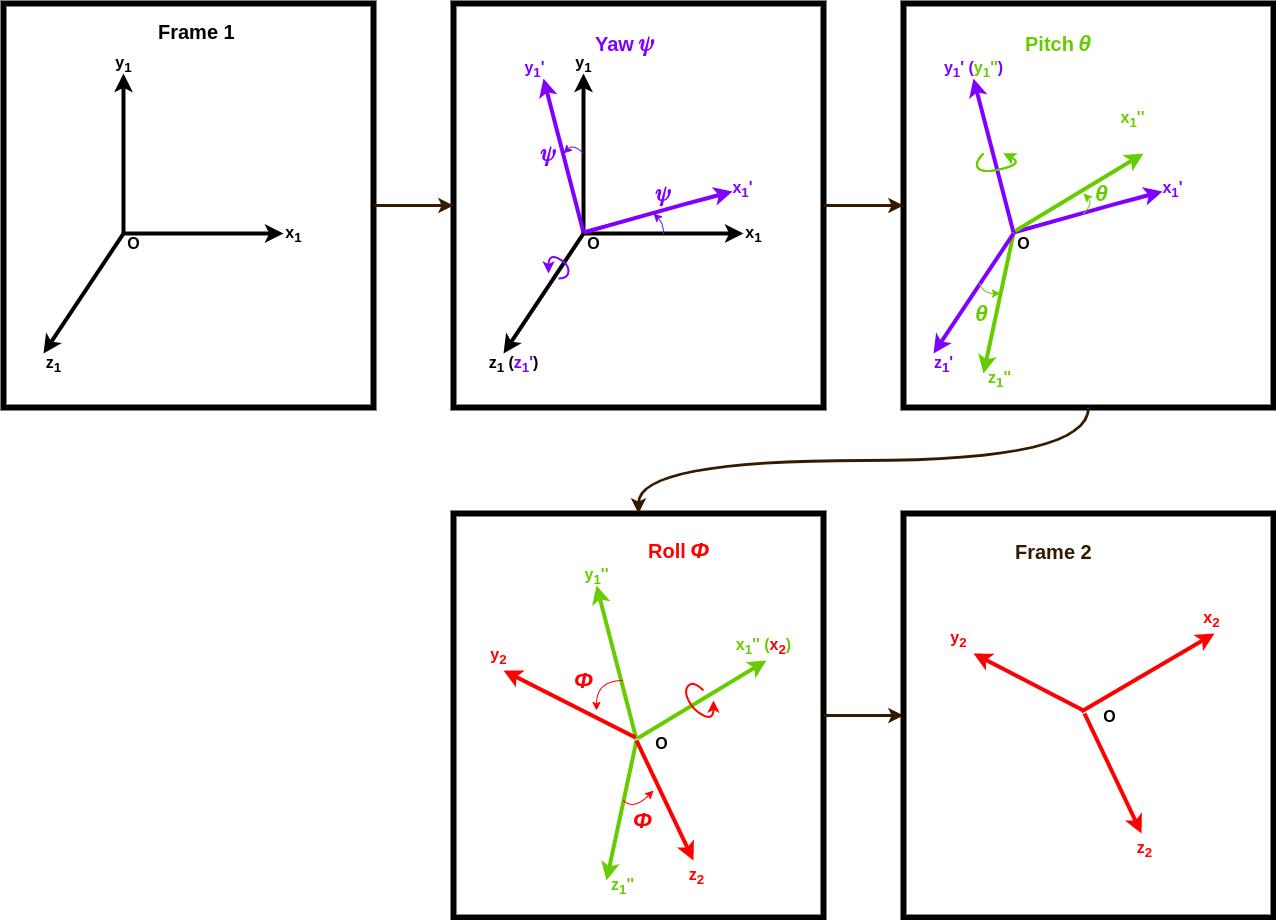
▲ 图1.1.1 三次旋转的过程
1.1.3 欧拉角范围
- 这个要具体问题具体对待。
- 假如是车体坐标系(
x-前,y-左,z-上),那么roll和pitch应该定义在(-90°,+90°),yaw应该定义在(-180°,+180°)。 - 假如是飞机坐标系,那么
roll、pitch和yaw都应该定义在(-180°,+180°)。 Eigen中的默认范围roll、pitch和yaw都是(-180°,+180°)。
1.2 旋转顺序
1.2.1 旋转顺序和旋转轴
- 对于x,y,z三个轴的不同旋转顺序一共有(x-y-z,y-z-x,z-x-y,x-z-y,z-y-x,y-x-z)六种组合,在旋转相同的角度的情况下不同的旋转顺序得到的姿态是不一样的。
- 比如,先绕x轴旋转alpha,再绕y轴旋转beta;先绕y轴旋转beta,再绕x轴旋转alpha。这两种顺序得到的姿态是不一样的。### 内旋和外旋
1.2.2 内旋和外旋
- 每次旋转是绕固定轴(一个固定参考系,比如世界坐标系)旋转,称为外旋。
- 每次旋转是绕自身旋转之后的轴旋转,称为内旋。
- 下图说明了内旋和外旋的区别。
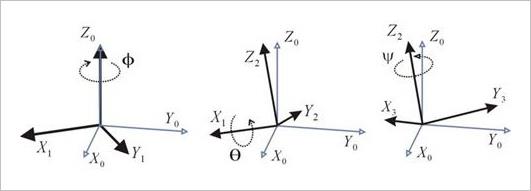
▲ 图1.2.1 内在旋转
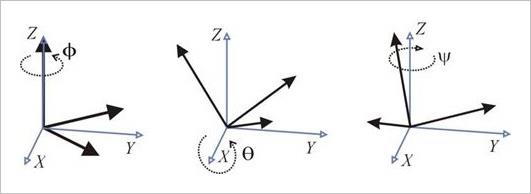
▲ 图1.2.2 外在旋转
按照内旋方式,Z-Y-X旋转顺序(指先绕自身轴Z,再绕自身轴Y,最后绕自身轴X),可得旋转矩阵(内旋是右乘)
R 1 = R z ( γ ) ⋅ R y ( β ) ⋅ R x ( α ) R_1 = R_z \\left( \\gamma \\right) \\cdot R_y \\left( \\beta \\right) \\cdot R_x \\left( \\alpha \\right) R1=Rz(γ)⋅Ry(β)⋅Rx(α)
按照外旋方式,X-Y-Z旋转顺序(指先绕固定轴X,再绕固定轴Y,最后绕固定轴Z),可得旋转矩阵(外旋是左乘):
R 2 = R z ( γ ) ⋅ R y ( β ) ⋅ R x ( α ) R_2 = R_z \\left( \\gamma \\right) \\cdot R_y \\left( \\beta \\right) \\cdot R_x \\left( \\alpha \\right) R2=Rz(γ)⋅Ry(β)⋅Rx(α)
故R1=R2,具体不在此证明,记住即可。这个结论说明ZYX顺序的内旋等价于XYZ顺序的外旋。
§02 旋转矩阵
2.1 由欧拉角到旋转矩阵
假设绕XYZ三个轴旋转的角度分别为 α , β , γ \\alpha ,\\beta ,\\gamma α,β,γ,则三次旋转的旋转矩阵计算方法如下:

▲ 图2.1 三个旋转矩阵
R x ( θ ) = [ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] R_x \\left( \\theta \\right) = \\beginbmatrix \\beginmatrix 1 & 0 & 0\\\\0 & \\cos \\theta & - \\sin \\theta \\\\0 & \\sin \\theta & \\cos \\theta \\\\\\endmatrix \\endbmatrix Rx(θ)=⎣⎡1000cosθsinθ0−sinθcosθ⎦⎤
R y ( θ ) = [ cos θ 0 sin θ 0 1 0 − sin θ 0 cos θ ] R_y \\left( \\theta \\right) = \\beginbmatrix \\beginmatrix \\cos \\theta & 0 & \\sin \\theta \\\\0 & 1 & 0\\\\ - \\sin \\theta & 0 & \\cos \\theta \\\\\\endmatrix \\endbmatrix Ry(θ)=⎣⎡cosθ0−sinθ010sinθ0cosθ转换矩阵平移矩阵旋转矩阵关系以及python实现旋转矩阵四元数欧拉角之间转换