matlab的音乐信号的分析与处理设计的实验咋做？

Posted 2023-05-07

一）设计内容与技术条件
1．截取一段音乐信号（2s左右），并对信号进行采样，画出采样后音乐信号的时域波形和频谱图；
2．用矩形窗设计一个FIR低通滤波器，确定滤波器的单位抽样响应，画出滤波器的频率响应（幅频响应和相频响应）曲线；（也可以根据自己需要设置滤波器性能指标）
低通滤波器设计性能指标：fp=100Hz,fs=120Hz,ap=20dB,as=1dB
3．用滤波器对采集到的音乐信号进行滤波，画出滤波以后信号的时域波形和频谱；
4．分析语音信号的变化，并回放语音信号；
5．运用GUI设计一个信号处理系统界面（选作）。

一、基本要求

    1 学会MATLAB的使用，掌握MATLAB的基本编程语句。

     2 掌握在Windows环境下音乐信号采集的方法。

     3 掌握数字信号处理的基本概念、基本理论和基本方法。

     4 掌握MATLAB设计FIR和IIR数字滤波器的方法。

5 掌握使用MATLAB处理数字信号、进行频谱分析、涉及数字滤波器的编程方法。

二、内容

     实验1音乐信号的音谱和频谱观察

     使用windows下的录音机录制一段音乐信号或采用其它软件截取一段音乐信号（要求：时间不超过5s、文件格式为wav文件）

①　使用wavread语句读取音乐信号，获取抽样率；（注意：读取的信号时双声道信号，即为双列向量，需要分列处理）；

②　输出音乐信号的波形和频谱，观察现象；

使用sound语句播放音乐信号，注意不同抽样率下的音调变化，解释现象。

 程序如下：

[Y,FS,NBITS]=WAVREAD('怒放的生命 - 汪峰5s'); %读取音乐信号

plot(Y);                                 %显示音乐信号的波形和频谱

sound(Y,FS);                             %听音乐（按照原来的抽样率）

Y1=Y(:,1);                               %由双声道信号变为单声道信号

size(Y1) 

figure

subplot(2,1,1);

plot(Y);                                 %显示原信号波形 

N=length(Y1);

f1=fft(Y1);                              %傅立叶变换

w=2/N*[0:N/2-1];

subplot(2,1,2);

plot(w,abs(f1(1:N/2)));                    %显示波形

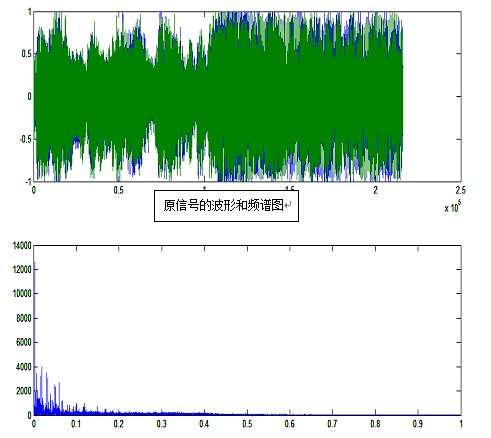
实验2音乐信号的抽取（减抽样）

①　观察音乐信号频率上限，选择适当的抽取间隔对信号进行减抽样（给出两种抽取间隔，代表混叠与非混叠）；

②　输出减抽样音乐信号的波形和频谱，观察现象，给出理论解释；

播放减抽样音乐信号，注意抽样率的变化，比较不同抽取间隔下的声音，解释现象

程序如下

[Y,FS,NBITS]=WAVREAD('怒放的生命 - 汪峰5s');

Y1=Y(:,1);

D=   ;j=0;                        %减抽样，D表示抽样间隔（10倍和100倍）

for i=1:D:length(Y1)               % I表示开始减抽样的起始点

    j=j+1;

    Y2(j)=Y1(i);                   %Y2减抽样后的信号

end

N=length(Y1);

N1=length(Y2);

F1=fft(Y1);

F2=fft(Y2);

w1=2/N*[0:N-1];

w2=2/N1*[0:N1-1];

figure

subplot(4,1,1);plot(Y1);          %显示原单声道信号波形和频谱

subplot(4,1,2);plot(Y2);          %图显示抽样信号波形和频谱

subplot(4,1,3);plot(w1,abs(F1));  %显示原单声道信号fft变换后的波形和频谱

subplot(4,1,4);plot(w2,abs(F2));  %显示抽样信号快速fft变换后的波形和频谱

sound(Y2,FS)                      %声音低沉，而且不是很清晰。有一些声音信号丢失，%抽样率越高，声音越听不清晰，

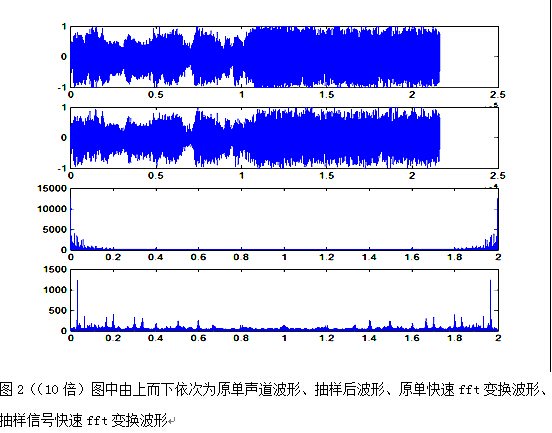
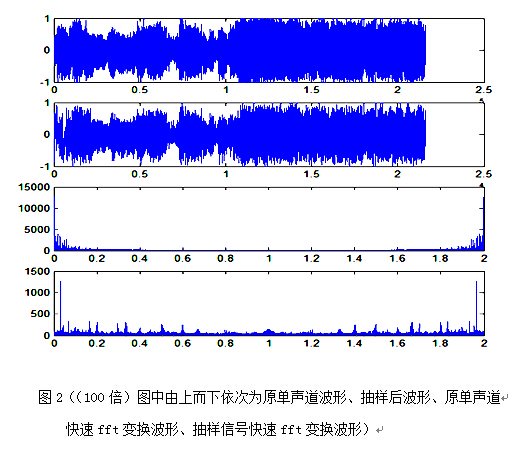
实验3   音乐信号的AM调制

①　观察音乐信号的频率上限，选择适当调制频率对信号进行调制（给出高、低两种调制频率）；

②　输出调制信号的波形和频谱，观察现象，给出理论解释；

播放调制音乐信号，注意不同调制频率下的声音，解释现象。

程序如下：

[Y,FS,NBITS]=WAVREAD('怒放的生命 - 汪峰5s');

Y1=Y(:,1);

N=length(Y1);

F1=fft(Y1);                                 %傅立叶变换

w1=2/N*[0:N/2-1];

figure

subplot(2,2,1);

plot(w1,abs(F1(1:N/2)));

N1=0:N-1;

Y2=cos(N1*pi/8);                            %设置高频调制信号

N2=length(Y2)

F2=fft(Y2);

w2=2/N2*[0:N2/2-1];

subplot(2,2,2);plot(w2,abs(F2(1:N2/2)));

subplot(2,2,3);stem((0:64),Y2(1:65)); 

F=Y1.*Y2';                                %利用高频调制信号调制单列音乐信号

N3=length(F);                             

F3=fft(F);                                %傅立叶变换

w3=2/N3*[0:N3-1];

subplot(2,2,4);plot(w3,abs(F3));

sound(F,FS)                        %  未混叠时，声音尖锐，不清晰，刺耳

                                    %   混叠时，声音轻，只有淡淡的音调，基本没有起伏，不清晰。

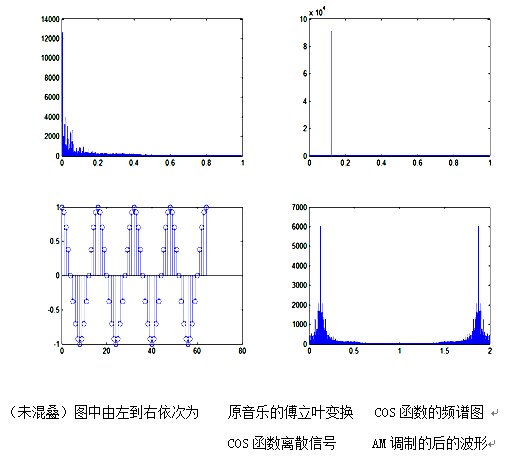
实验4 AM调制音乐信号同步解调

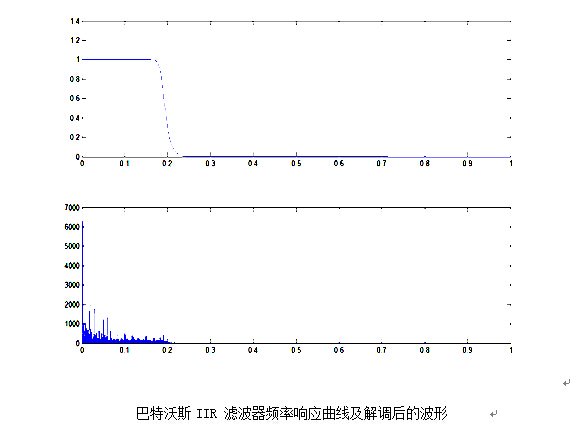
①　设计巴特沃斯IIR滤波器完成同步解调；观察滤波器频率响应曲线

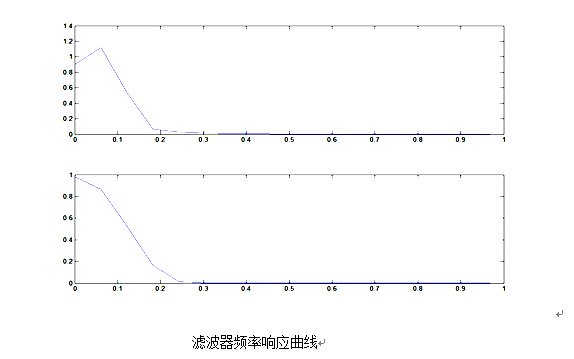
②　用窗函数法设计FIR滤波器完成同步解调，观察滤波器频率响应曲线；（分别使用矩形窗和布莱克曼窗，进行比较）；

③　输出解调信号的波形和频谱图，观察现象，给出理论解释；

播放解调音乐信号，比较不同滤波器下的声音，解释现象。

巴特沃斯IIR 滤波器

  程序如下

clear all;close all;clc

[Y,FS,NBITS]=WAVREAD('怒放的生命 - 汪峰5s');

Y1=Y(:,1);

N=length(Y1);

N1=0:N-1;

Y2=cos(N1*pi/8);   

F=Y1.*Y2';

F2=F.*Y2';                     %音乐信号调制

 

wp=0.18;ws=0.25;rp=1;rs=50;     %设计巴特沃斯IIR 滤波器

[N4,Wc]=buttord(wp,ws,rp,rs);

[B,A]=butter(N4,Wc);

[Hd,w]=freqz(B,A);

figure

subplot(2,1,1);plot(w/pi,abs(Hd));

 

F3=filter(B,A,F2);             %解调音乐信号

N4=length(F3);

F4=fft(F3);

w4=2/N4*[0:N4/2-1];

subplot(2,1,2);plot(w4,abs(F4(1:N4/2)));

sound(F3,FS)                       %声音清晰，基本和原来的音乐差不多，但是音乐开始有一点点杂音。

矩形窗和布莱克曼窗

function hd=ideal(N,wc)

for n=0:N-1

    if n==(N-1)/2

        hd(n+1)=wc/pi;

    else hd(n+1)=sin(wc*(n-(N-1)/2))/(pi*(n-(N-1)/2));

    end

end

（将上述程序保存为ideal.m,但是不能运行。然后在打开新窗口编写下列主程序）

 

clear all;close all;clc

[Y,FS,NBITS]=WAVREAD('怒放的生命 - 汪峰5s');

Y1=Y(:,1);

N=length(Y1);

N1=0:N-1;

Y2=cos(N1*pi/8);   

F=Y1.*Y2';

F2=F.*Y2';                     %调制音乐信号

 

N=89;wc=pi/0.22;                 % 矩形和布莱克曼窗  

hd=ideal(N,wc);

w1=boxcar(N);

w2=blackman(N);

h1=hd.*w1';

h2=hd.*w2';

N1=length(h1);

N2=length(h2);

fh1=fft(h1);

fh2=fft(h2);

ww1=2/N1*(0:(N1-1)/2);

ww2=2/N2*(0:(N2-1)/2);

figure

subplot(2,1,1);plot(ww1,abs(fh1(1:(N1-1)/2+1)));

subplot(2,1,2);plot(ww2,abs(fh2(1:(N1-1)/2+1)));

 

F3=conv(F2,h1);           

F4=conv(F2,h2);

M1=length(F3);

M2=length(F4);

fy1=fft(F3);

fy2=fft(F4);

w3=2/M1*[0:M1/2-1];

w4=2/M2*[0:M2/2-1];

figure

subplot(2,1,1);plot(w3,abs(fy1(1:M1/2)));

subplot(2,1,2);plot(w4,abs(fy2(1:M2/2)));

 

sound(F3,FS)             %音乐信号清晰，有杂音，低沉.

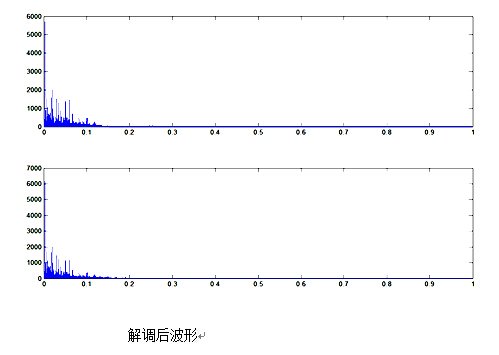
5、音乐信号的滤波去噪

①　给出原始音乐信号叠加幅度为0.05，频率为3kHz，5kHz、8kHz的三余弦混合噪声，观察噪声频谱以及加噪后音乐信号的音谱和频谱，并播放音乐，感受噪声对音乐信号的影响；

②　给原始音乐信号叠加幅度为0.5的随机白噪声（可用rand语句产生），观察噪声频谱以及加噪后音乐信号的音谱和频谱，并播放音乐，感受噪声对音乐信号的影响；

根据步骤①、②观察到的频谱，选择合适指标设计滤波器进行滤波去噪，观察去噪后信号音谱和频谱，并播放音乐，解释现象。

程序如下：

三余弦混合噪声：

[x,fs,nbits]=wavread('怒放的生命 - 汪峰5s');

x1=x(:,1);               %获取单列音乐信号并对其做FFT变换

N1=length(x1);

fx1=fft(x1);

w1=2/N1*[0:N1/2-1];

 

n=0:N1-1;y=0.05*(cos(2*pi*n*3000/fs)+cos(2*pi*n*5000/fs)+cos(2*pi*n*8000/fs));

                         %设计三余弦混合噪声信号

N2=length(y);            %对三余弦混合噪声信号做FFT变换

fy=fft(y);

w2=2/N2*(0:N2/2-1)*fs/2;

 

hdx=x1+y';               %产生加噪后的音乐信号并对其做FFT变换

M=length(hdx);            

fhdx=fft(hdx);

w3=2/M*(0:M/2-1);

 

figure           %画出单列信号音乐信号的频谱图、三余弦混合噪声信号的离散信号图

                  %及其频谱图和加噪后音乐信号的频谱图

subplot(2,2,1);plot(w1,abs(fx1(1:N1/2)));

subplot(2,2,2);stem((0:127),y(1:128));

subplot(2,2,3);plot(w2,abs(fy(1:N2/2)));

subplot(2,2,4);plot(w3,abs(fhdx(1:M/2)));

sound(hdx,fs);         %  音乐信号有电流声，而且噪声比较明显。

 

wp=0.1;ws=0.15;rp=1;rs=50;  %设计巴特沃斯滤波器

[N4,Wc]=buttord(wp,ws,rp,rs);

[B,A]=butter(N4,Wc);

[Hd,w]=freqz(B,A);

 

lohdx=filter(B,A,hdx);     %利用巴特沃斯滤波器对加噪后音乐信号进行滤波并对其做%FFT变换

M1=length(lohdx);

flohdx=fft(lohdx);

w4=2/M1*(0:M1/2-1);

 

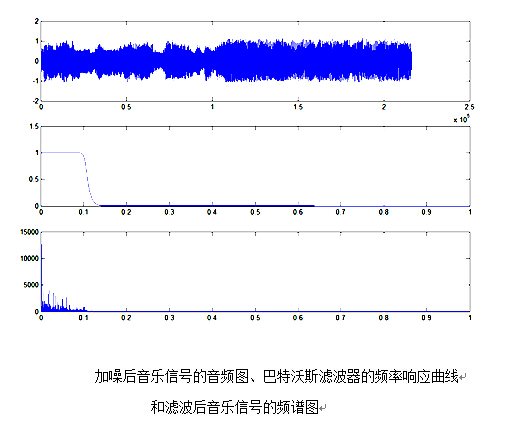
figure               %画出加噪后音乐信号的音频图、巴特沃斯滤波器的频率响应曲线

                      %和滤波后音乐信号的频谱图

subplot(3,1,1);plot(hdx);

subplot(3,1,2);plot(w/pi,abs(Hd));

subplot(3,1,3);plot(w4,abs(flohdx(1:M1/2)));

sound(lohdx,fs);           %滤波后音乐信号比较低沉，较清晰。

 

白噪声：

[x,fs,nbits]=wavread('怒放的生命 - 汪峰5s');

x1=x(:,1);               %获取单列音乐信号并对其做FFT变换

N1=length(x1);

fx1=fft(x1);

w1=2/N1*[0:N1/2-1];

ry=rand(size(x1))-0.5;            %产生随机白噪声信号并对其做FFT变换

N=length(ry);

fry=fft(ry);

w=2/N*(0:N-1);

 

xry=x1+ry;                       %产生加噪后的音乐信号并对其做FFT变换 

NN=length(xry)

fxry=fft(xry);

ww=2/NN*(0:NN/2-1);

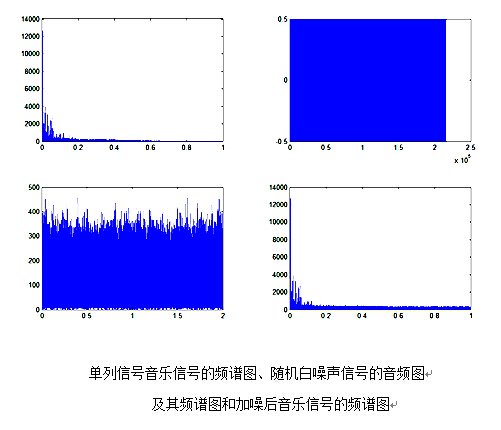
figure                   %画出单列信号音乐信号的频谱图、随机白噪声信号的音频图

                          %及其频谱图和加噪后音乐信号的频谱图

subplot(2,2,1);plot(w1,abs(fx1(1:N1/2)));

subplot(2,2,2);plot(ry);

subplot(2,2,3);plot(w,abs(fry));

subplot(2,2,4);plot(ww,abs(fxry(1:NN/2)));

sound(xry,fs);             %声音信号有沙沙声。

 

wp=0.1;ws=0.15;rp=1;rs=50;      %设计巴特沃斯滤波器

[N4,Wc]=buttord(wp,ws,rp,rs);

[B,A]=butter(N4,Wc);

[Hd,w]=freqz(B,A);

 

loxry=filter(B,A,xry);          %利用巴特沃斯滤波器对加噪后音乐信号进行滤波并对%其做FFT变换 

NN1=length(loxry);

floxry=fft(loxry);

ww1=2/NN1*(0:NN1/2-1);

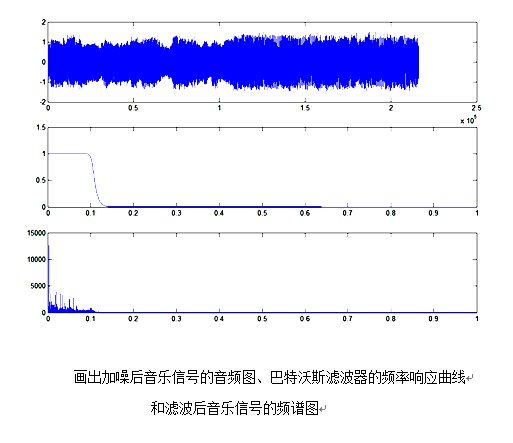
figure              %画出加噪后音乐信号的音频图、巴特沃斯滤波器的频率响应曲线

                         %和滤波后音乐信号的频谱图

subplot(3,1,1);plot(xry)

subplot(3,1,2);plot(w/pi,abs(Hd));

subplot(3,1,3);plot(ww1,abs(floxry(1:NN1/2)));

%sound(loxry,fs);            %音乐信号低沉，但是沙沙声还是没有滤除。但是较为减轻

6、音乐信号的幅频滤波及相频分析

①　设计低通滤波器（可自行选取不同的截止频率），滤除原始音乐信号的高频信息，观察滤波前后的幅度频谱，并比较滤波前后的音乐效果，感受高频信息对音乐信号的影响；

②　设计高通滤波器（可自行选取不同的截止频率），滤除原始音乐信号的低频信息，观察滤波前后的幅度频谱，并比较滤波前后的音乐效果，感受低频信息对音乐信号的影响；

③　选取两段不同的音乐信号，分别将其幅度谱与相位谱交叉组合构成新的音乐信号，播放比较组合后的音乐与原始音乐，感受相频信息对音乐信号的影响。

 

程序如下;

滤除高频信息的程序：

 clearall;close all;clc

[x,fs,nbits]=wavread('怒放的生命 - 汪峰5s');

x1=x(:,1);            %获取单列音乐信号并对其做FFT变换

N=length(x1);

fx1=fft(x1);

w1=2/N*(0:N/2-1);

 

wp=0.01;ws=0.06;rp=1;rs=50;  %设计巴特沃斯滤波器

[N4,Wc]=buttord(wp,ws,rp,rs);

[B,A]=butter(N4,Wc);

[Hd,w]=freqz(B,A);

 

lox1=filter(B,A,x1);         %使用巴特沃斯滤波器滤除音乐信号的高频部分并对所得

%音乐信号做FFT变换

N1=length(lox1);

flox1=fft(lox1);

w2=2/N1*(0:N1/2-1);

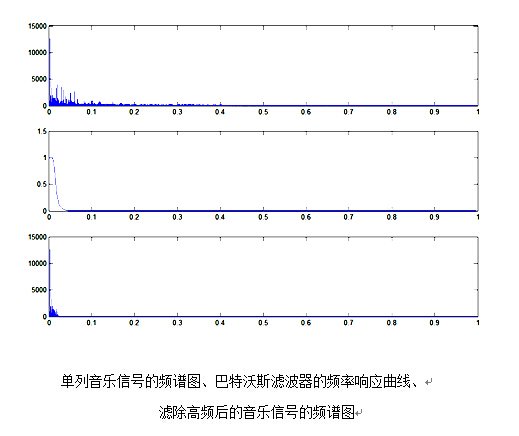
figure           %画出单列音乐信号的频谱图、巴特沃斯滤波器的频率响应曲线和滤除

 %高频后的音乐信号的频谱图

subplot(3,1,1);plot(w1,abs(fx1(1:N/2)));

subplot(3,1,2);plot(w/pi,abs(Hd));

subplot(3,1,3);plot(w2,abs(flox1(1:N1/2)));

sound(x1,fs);   %播放单列音乐信号和滤除高频后的音乐信号

sound(lox1,fs)；%声音清晰

滤除低频信息的程序：

clear all;close all;clc

[x,fs,nbits]=wavread('怒放的生命 - 汪峰5s');

x1=x(:,1);            %获取单列音乐信号并对其做FFT变换

N=length(x1);

fx1=fft(x1);

w1=2/N*(0:N/2-1);

 

wp=0.2;ws=0.05;rp=1;rs=50;  %设计巴特沃斯高通滤波器

[N4,Wc]=buttord(wp,ws,rp,rs);

[B,A]=butter(N4,Wc,'high');

[Hd,w]=freqz(B,A);

 

lox1=filter(B,A,x1);         %使用巴特沃斯滤波器滤除音乐信号的低频部分并对所得音乐信号做FFT变换

N1=length(lox1);

flox1=fft(lox1);

w2=2/N1*(0:N1/2-1);

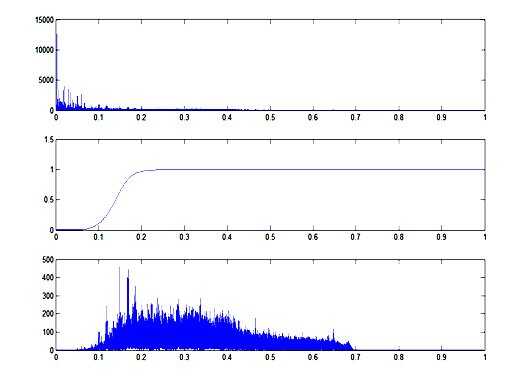
figure                    %画出单列音乐信号的频谱图、巴特沃斯滤波器的频率响应曲

%线和滤除低频后的音乐信号的频谱图

subplot(3,1,1);plot(w1,abs(fx1(1:N/2)));

subplot(3,1,2);plot(w/pi,abs(Hd));

subplot(3,1,3);plot(w2,abs(flox1(1:N1/2)));

sound(lox1,fs);                      %声音低，不清晰。

交叉组合音乐

clear all;close all;clc

clear all;close all;clc

[x,fs,nbits]=wavread('钢琴曲 - 雨的印记5s');

[y,fs,nbits]=wavread('怒放的生命 - 汪峰5s');

x1=x(:,1); 

y1=y(:,1);

x2=x1(1:200000)                   %取音乐长度

Nx2=length(x2);

y2=y1(1:200000);

Ny2=length(y2);

x3=fft(x2);

y3=fft(y2);

w1=2/Nx2*[0:Nx2-1];

w2=2/Ny2*[0:Ny2-1];

 

 

Fx1=abs(x3);                         %选取第一个音乐信号的幅度和第二个音乐信号%的相位

Ay1=angle(y3);

 

F4=Fx1.*exp(j*Ay1);                     

X4=ifft(F4);

NF4=length(F4);

F5=fft(F4);

w3=2/NF4*[0:NF4-1];

 

sound(real(X4),fs);

                       figure

subplot(3,1,1);plot(w1,abs(x3));         

subplot(3,1,2);plot(w2,abs(y3));         

subplot(3,1,3);plot(w3,abs(F5));

参考技术A 语音信号的采集和频谱分析：
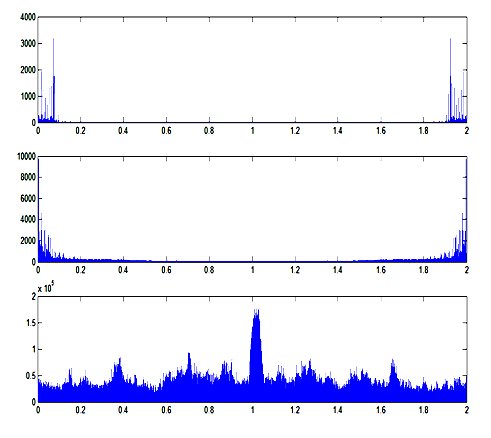
[y,fs,bits]=wavread('voice'); %读取音频信息（双声道，16位，频率44100Hz）
sound(y,fs,bits); %回放该音频
Y=fft(y,4096); %进行傅立叶变换
subplot(211);
plot(y);
title('声音信号的波形');
subplot(212)
plot(abs(Y));
title('声音信号的频谱');

用MATLAB设计对信号进行频谱分析和滤波处理的程序

设计出一套完整的系统，对信号进行频谱分析和滤波处理；
1．产生一个连续信号，包含低频，中频，高频分量，对其进行采样，进行频谱分析，分别设计三种高通，低通，带通滤波器对信号进行滤波处理，观察滤波后信号的频谱。

采样没什么，就是产生一个连续的（实际还是数字信号），实际上就是再进行一下抽取。
变化就用fft函数。
滤波器设计有专门的函数来实现，IIR的有巴特沃斯、切比雪夫、椭圆等等。FIR可以直接在频域设计，应该也有专门的函数，忘了。高通就是用1减去低通，带通就是高通加低通减1，当然这是比较投机的方法，数字信号处理在FIR设计里有专门讲几种滤波器的设计。 参考技术A help fft 参考技术B 我也在关注怎么用simulink画出频谱图来，就是现在用scope看到时域图了，怎么弄出频谱图来呢？