数电基础：时序逻辑电路的时序分析

Posted 2023-05-05

参考技术A 目录

1.组合逻辑延迟

2.时钟输出延迟Tco

3.同步系统中时钟频率

3.1 建立时间与保持时间都满足

3.2 建立/保持时间不满足

（1） Tcomb太大导致建立时间不满足

（2） 器件的固有保持时间增大（老化）使得保持时间违例

4. 时钟偏斜及其影响

4.1时钟偏斜的物理意义

4.2 时钟偏斜对时序的影响

（1） 对于未引入时钟偏斜时，保持时间与建立时间均不为例必要条件：

（2）引入时钟偏斜后的时序图如下（Tskew21>0）

（3）引入时钟偏斜也可能会导致保持时间违例，进而输出亚稳态的情况（Tskew21>0）

（4）Tskew21 <0时，即clk2先于clk1到达其时钟端，保持时间就比较容易满足了，但对满足建立时间就有所要求了。

4.3实例介绍

1.组合逻辑延迟

布线延迟与门延迟

    数字逻辑电路中，任何输出信号到输入信号之间都有一定的线路延迟，把这种线路延迟叫做布线延迟。当数字逻辑电路经过门电路时，同样会造成一定的延迟，我们把这个延迟叫做门延迟。

图1布线延迟

图2：门延时

2.时钟输出延迟Tco

    clock to out的时间，即从时钟触发到数据输出的时间。这是针对触发器器件而言，是触发器的固有参数，不同厂家或不同批次的器件 该参数有差异。

图3：Tco

3.同步系统中时钟频率

图4：同步系统典型电路图

Tsu      :  触发器建立时间

Th        ： 触发器保持时间

T          ： 电路的工作周期

Tco      :  时钟输出延迟

Tskew ： 时钟偏斜(clock skew)，又称为时钟偏移，是指时钟信号到达数字电路各部分所用时间差异。

Tcomb： 组合逻辑的延迟。

                                                                            时钟偏移Skew = 0

    为由浅入深，假设 Skew = 0，即说明时钟到达所有器件的时间相同，没有差异，那么图中时钟上升沿1到时钟上升沿2之间刚好相隔一个工作周期T。下面介绍几种情况下的同步时序电路模型的时序图，图中标注了说明。

3.1 建立时间与保持时间都满足

    下图为同步时序电路模型时序图1（Tskew=0，建立时间和保持时间都满足）：

图6：建立保持时间时序图1分析

核心知识点：

(1) Tco+Tcomb将导致数据会延迟到达下一个触发器，要想数据到达下一个触发器时满足建立时间的要求，则必要条件为：

T-(Tco+Tcomb)>Tsu，即有T>Tco+Tcomb+Tsu。因此一个电路搭建好后，会有一个最小的工作周期Tmin=Tco+Tcomb或者最大的工作频率1/Tmin。

(2) 一般电路的工作时钟不是其所能跑的最高频率，那么其实际工作周期要大于其支持的最小工作周期，这个差值就是建立时间的裕量Ts_slack。反映在计算公式上即为：Ts_slack=T-Tmin=T-(Tco+Tcomb)。会不会出现T-(Tco+Tcomb)<Tsu呢？这不就是建立时间违例的情况吗？怎么解决呢？看下面分析。

(3) Tco+Tcomb将会导致数据延迟到达下一个触发器，而下一个触发器不仅仅要求数据提前到达保持稳定一段时间，还要求数据被打入后保持一段时间稳定。假设数据源变化速率很慢，慢于时钟速率问题不大因为相邻周期触发器采样的是同一个值送往下一个寄存器，但同步系统中，数据一般跟随时钟同步跳转，即一个cycle会跳变一次，即数据保持一个时钟周期T的稳定状态。如此，本级寄存器在当前时钟采样的数据经过Tco+Tcomb延迟后到达下一级触发器，那么数据在下级触发器在下次时钟上升沿被打入后仍然会保持Tco+Tcomb时间。下级触发器要想满足保持时间，其必要条件为：Tco+Tcomb>Th .

(4)一般Tco+Tcomb不可能刚好等于Th的，因此当Tco+Tcomb大于Th，那么Th-slack =Tco+Tcomb-Th。会不会出现Tco+Tcomb小于Th呢？这不就是保持时间违例的情况吗，遇到这种情况怎么办呢？下面也有介绍。

综上：要想时序收敛，就是建立保持时间不违例，二者缺一不可。

3.2 建立/保持时间不满足

（1） Tcomb太大导致建立时间不满足

      下图为同步时序电路模型时序图2（Tskew =0，组合逻辑延迟太大，导致建立时间不能满足）：

图7：建立时间违例时序图2分析

  解决1：可通过降频（增大周期）以满足建立时间

      下图为同步时序电路模型时序图3（Tskew = 0，增加时钟周期以满足建立时间）：

图8：时钟频率降频

解决2：优化组合逻辑

解决3：切割组合逻辑

详见：如何提高电路工作频率

（2） 器件的固有保持时间增大（老化）使得保持时间违例

图9：保持时间违例时序图分析

解决：当不满足保持时间时，通过增大组合逻辑延迟Tcomb来是保持时间满足

图10：保持时间违例解决

                                                                            当 Tskew不等于0

之前为了简单介绍知识点 ，未引入时钟偏移Tskew，但时间电路中是存在时间偏移的，分析时候不可忽视。

4. 时钟偏斜及其影响

图11

4.1时钟偏斜的物理意义

              时钟偏移指定了同时发生的两个时钟信号经过时钟驱动器或布线后到达时间上的差异。

4.2 时钟偏斜对时序的影响

            下图给出了未引入和引入时钟偏斜（clock skew）后的同步时序电路图对比模型:

图12

（1） 对于未引入时钟偏斜时，保持时间与建立时间均不为例必要条件：

                  保持时间不违例：Tco+Tcomb > Th；

                  建立时间不违例：T>Tco+Tcomb+Tsu。

          因此不会产生输出亚稳态现象。也可推出 (T-Tco-Tsu) >  Tcomb > (Th-Tco) ，即对组合逻辑延迟的要求。

  【注意】：这里面只有时钟周期T和组合逻辑延迟Tcomb可变。

（2）引入时钟偏斜后的时序图如下（Tskew21>0）

            图12中，由于引入了Tskew21（>0）,导致FF2的时钟段clk2的时序相对于FF1的clk1延后了Tskew，但上图的情况属于并未导致保持时间违例，因此未发生输出亚稳态现象。

            仔细分析就可以看出，相对于未引入时钟偏斜时的保持时间裕量（Th-slack = Tco+Tcomb-Th）。此情况中FF2的保持时间裕量变成了Th-slack = Tco+Tcomb-Th-Tskew21，减少了Tskew21。（原因就clk2滞后Tskew21,导致保持时间的起点和终点相对于数据延后了）。

                    1.保持时间不违例：Tco+Tcomb-Tskew21>Th

                                即依旧有Th-slack=Tco+Tcomb-Th-Tskew21>0，即Tco+Tcomb-Tskew21>Th ;

                      2.建立时间不违例：T+Tskew21>Tco+Tcomb+Tsu

            只要未引入时钟偏移的时候（Tskew21 == 0）的时候,就满足建立时间要求 T>Tco + Tcomb +Tsu，那么引入Tskew后，时钟  Clk2相对于数据滞后，更能够满足建立时间了。甚至之前尚不满足建立时间要求即T < Tco + Tcomb + Tsu情况下，在引入  Tskew后，就有T+Tskew > Tco +Tcomb + Tsu满足了建立时间。

（3）引入时钟偏斜也可能会导致保持时间违例，进而输出亚稳态的情况（Tskew21>0）

        1.保持时间违例：Tco+Tcomb-Tskew21<Th

                当引入的 Tskew21不够大时，没有超过保持时间裕量问题不大，但如果Tskew21太大，Tskew21>Tco+Tcomb-Th=Th-slack(未引入偏移时的裕量)，就不再满足保持时间的要求，也会导致输出亚稳态。如下图所示；

        2.建立时间必然不违例

                如情况（2）种描述，只要在未引入时钟偏移的情况下满足建立时间，那么只要Tskew21>0就会必定不违例。并且建立时间的裕量： Ts_slack =Tskew+ (T - Tco -Tcomb -Tsu)增加了Tskew。（情况（2）的建立时间也是如此，在此补充一下）

（4）Tskew21 <0时，即clk2先于clk1到达其时钟端，保持时间就比较容易满足了，但对满足建立时间就有所要求了。

          1.保持时间必然不违例

                因为在未引入偏移时候就有Tco+Tcomb > Th，只要Tskew21<0，则Tco+Tcomb-Tskew21 >Th必然满足。

            2. 建立时间不违例：T+Tskew21  >  Tco+Tcomb+Tsu

            需要注意的是此时的Tskew21 < 0，因此 T > Tco+Tcomb+Tsu-Tskew21，此时最小时钟周期Tmin=Tco+Tcomb+Tsu-Tskew21 变大了，支持的最大时钟频率减小了。

标题

（5）同理，当Tskew21<0  并且T+Tskew21 < Tco+Tcomb+Tsu , 此时建立时间就违例了，就会产生输出亚稳态现象了。

4.3实例介绍

Ex1:

      通常我们可以假设逻辑门的延时为1+0.1k，其中k为逻辑门的输入端个数。比如对于非门，只有一个输入端，那么其延时为1+1*0.1=1.1ns。现有触发器的时序参数为:Tsu=0.6ns, Th=0.4ns, 0.8ns ≤ Tco ≤ 1.0 ns , 需要计算下面电路的最小时钟周期：

答：  Tclkmin =Tco-max+Tcomb-max+Tsu=1.0+1.1+0.6=2.7ns。所以该电路最高可跑时钟频率为fmax=1/Tclkmin=370.37Mhz。

Ex2: 4位计数器电路如下图所示：

电路中有很多电路中有很多路径可以使触发器开始（Enable）或结束（Disable），其中最长的路径开始于触发器Q0结束语Q3。电路中这种最长的路径称为关键路径。如上图中红色路线，包括触发器Q0的时钟信号输出至Q的延时Tco，3个与门，1个异或门以及建立时间Tsu，所以有：

                    Tclkmin = Tco+3* Tand+Txor+Tsu=1.0+3*1.2+1.2+0.6=6.4ns

        fmax = 1/Tclkmin =156.25Mhz

  电路的最短路径是每个触发器经过一个异或门到它自身，每条这样的路径的最小延时为Tco+Txor=0.8+1.2=2.0ns>Th=0.4ns, 所以电路中不存在时间违背。

Ex3：在上述Ex2中，是假定时钟clk是同时到达4个触发器的，即时钟clk不存在clock skew、现在我们仍然假设时钟信号clk同时到达Q0、Q1、Q2，但是到达Q3存在一个延时。这种时钟信号到达触发器的时间偏离称为时钟偏斜（clock skew）。关键路径为Q0到Q3，然而Q3的时钟偏斜具有减小延迟的作用。原因在于数据加载到触发器之前就额外的时间，将时钟偏斜skew=1.5ns计算在内，从Q0到Q3的路径上时延为：      Tco+3*Tand+Txor+Tsu-Tskew=6.4-1.5=4.9ns（之前的时延为6.4ns）。此时从Q0到Q2的线路径成为关键路径：Tclkmin =Tco+2*Tand+Txor+Tsu=1.0+2*1.2+1.2+0.6=5.2ns，

fmax =1/Tclkmin =192.31Mhz。这种情况下，时钟偏斜会提高时钟频率，但如果时钟偏斜是负的，则会降低时钟频率。

由于时钟偏斜的存在，数据加载到Q3会被延迟，对于所有开始于Q0，Q1，Q2而结束于Q3的路径，加载的延时会提高触发器维持时间的要求(Th+Tskew)，其中最短的路径是从Q2到Q3，延迟为Tco + Tand + Txor = 0.8+ 1.2+1.2=3.2ns > Th+Tskew=1.9ns,所以不存在时间违背。

      对于时钟偏斜值Tskew >= 2.8ns情况，可以看出存在时间违背，此时不论时钟频率多少，该电路都不可能可靠的工作。

    我们再看下面这个例子，在这个电路中有一条路径开始于触发器Q1, 经过一些逻辑门网络，在触发器Q2的D端结束。由图可知，时钟信号到达触发器前存在不同的延迟。假设触发器Q1和Q2的时钟信号延迟分别为t1和t2，这两个触发器之间的时间偏斜可定义为Tskew= t2-t1,假设电路中通过逻辑门路径的最长延迟为TL,则这两个触发器的最小时钟周期为Tclk-min=Tco+TL+Tsu-Tskew，　因此如果t2-t1>0，则时钟频率会提升，否则时钟偏斜会降低频率。

为了计算触发器Q2是否存在时间违背，需要确定触发器的最短路径。如果电路中通过逻辑门的最小延迟为Tl,且Tl+Tco<Th+Tskew, 将会产生时间违背。如果t2-t1>0,维持时间的限制将更难以满足，而如果t2-t1<0,则较易满足。

原文链接：https://blog.csdn.net/qq_26652069/article/details/90756790

2017.0404.数字电路与系统-时序逻辑电路

1.时序逻辑电路由两个部分组成，为什么前面介绍了触发器，就是为了这里的时序逻辑电路做准备的。时序逻辑电路的两部分一个是组合逻辑电路，一个存储部分。存储部分就是触发器组成的。相应的时序逻辑电路的输出也就由两个部分组成，一个是组合逻辑电路的输出，另个一个是存储部分的输出。还有一点需要注意的是，时序电路估计比较复杂，不太容易画出逻辑图，因此只能抽象地画出两个组成部件。

2.存储器是由多个存储单元组成的，这里的存储单元就是触发器。

3.假设某一个时序逻辑电路有n个外输入，m个外输出，k个存储单元，那么某个 i 外输出为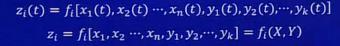  

从这个等式可以看出一些思想：为什么说数字电路的设计和系统是属于计算机编程底层的知识？编程时，工作人员只需要编好相应的程序，逻辑功能，具体怎样实施，怎样简洁地实施，这都和编程人员无关。逻辑功能抽象到底，就是多元的函数等式，有众多的自变量，因变量。在这里，我可不可以发散的想一下，为什么说算法挺重要，估计算法就是直接将逻辑功能的这种函数等式表达出来，而入门级别的程序员干的活只是一个频繁地调用别用设计好的东西，没什么技术含量，只要知道有什么，自己需要什么，最后直接调用即可。但是，现在作为一个学习数字电路的人来说，可能到最后，自己依旧无法设计出符合要求的数字电路，但是你能清楚这其中的运作机制，那有助于对上层运作的了解。抛开上面的题外话，每一个输出都是所有输入的函数，计算机还是一个数学为核心的学科。这里还有一点，为什么要有那么多的输出，我可以理解为每一个输出代表着一个逻辑功能，同一个电路中，越多的输出可以减少电路的成本，也可以展现更多的逻辑功能。

4.仔细地看下面的这张时序逻辑电路的抽象图，我除了想说触发器在时序逻辑电路中起到了存储作用外，还将触发器反馈的特点清晰地表现了出来。时序逻辑电路的两个组成部件联系很紧密，组合逻辑电路给存储器提供了内输入，存储器又反馈给时序逻辑电路整个外输入。

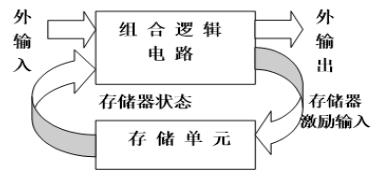
5.在时序逻辑电路中，有这么几个概念，外输入，内输入，外输出，内输出。这几个概念不弄清楚，对于时序逻辑电路的理解就不会深刻。存储器是由内输出得到的内输入信号，内输入信号要反馈到时序逻辑电路中，作为整个电路的部分激励信号来看待。内输入和内输出的命名都是针对时序逻辑电路而言的，这种命名对存储器不利。

我们回过头来再看当时的方程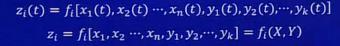，这个方程是即可输出方程，意味着所有的外输入和内输入一确定，那么时序逻辑电路的输出就确定了，内输入和外输入两者间是分开来看的，，从某种程度上来说，内输入是由外输入决定的，内输入本质上是反馈。

为什么时序逻辑电路的外输出是即刻输出方程，这里面是否和时序逻辑电路的逻辑功能有关系？

6.现在仔细研究存储器，在整个时序逻辑电路中，组合逻辑电路较为死板，研究的意义不大，但是信号在存储器里面的回路就比较值得研究了。相较于外输出的即刻输出方程，存储器的方程称之为激励方程或驱动方程。触发器由k个存储单元组成，那么就存在k个驱动方程，