求解啊, C语言的一个问题

Posted 2023-04-27

#include<stdio.h>
int main (void)

int a = 1, b =4, c = 6, x, y;
y=(x=a+b),(b+c);
printf("y=%d, x=%d", y,x);
return 0;

为什么输出的结果试Y=5,X=5啊.????

表达式y=(x=a+b),(b+c);中逗号运算符结合方式从左到右且括号最高，所以首先计算(x=a+b)表达式，得到x=5而且(x=a+b)的值为5，故原始可写为y=5,(b+c);然后计算表达式(b+c),得到表达式的值为10，故原表达式可以写为y=5,10;,而逗号表达式优先级比赋值运算低，故先赋值，y=5,然后原表达式变为了5,10;逗号运算符的值是最右边一个表达式的值，所以得到整个y=(x=a+b),(b+c);表达式的的值为10，虽然整个表达式的值为10但是x=5，y=5。 参考技术A 这个是因为逗号的优先级实在低的一塌糊涂，最低！
y=(x=a+b),(b+c);
本质是
(y=(x=a+b)),(b+c);
b+c的值根本没给y

应该改为
y=((x=a+b),(b+c));

以下是优先级表，还有结合性，L和R表示左结合和右结合，还有作用和用法，摘自c++ primer

L
::
global scope（全局作用域）
:: name

L
::
class scope（类作用域）
class :: name

L
::
namespace scope（名字空间作用域）
namespace :: name

L
.
member selectors（成员选择）
object . member

L
->
member selectors（成员选择）
pointer -> member

L
[]
subscript（下标）
variable [ expr ]

L
()
function call（函数调用）
name (expr_list)

L
()
type construction（类型构造）
type (expr_list)

R
++
postfix increment（后自增操作）
lvalue++

R
--
postfix decrement（后自减操作）
lvalue--

R
typeid
type ID（类型 ID）
typeid (type)

R
typeid
run-time type ID（运行时类型 ID）
typeid (expr)

R
explicit cast（显式强制类型转换）
type conversion（类型转换）
cast_name <type>(expr)

R
sizeof
size of object（对象的大小）
sizeof expr

R
sizeof
size of type（类型的大小）
sizeof(type)

R
++
prefix increment（前自增操作）
++ lvalue

R
--
prefix decrement（前自减操作）
-- lvalue

R
~
bitwise NOT（位求反）
~expr

R
!
logical NOT（逻辑非）
!expr

R
-
unary minus（一元负号）
-expr

R
+
unary plus（一元正号）
+expr

R
*
dereference（解引用）
*expr

R
&
address-of（取地址）
&expr

R
()
type conversion（类型转换）
(type) expr

R
new
allocate object（创建对象）
new type

R
delete
deallocate object（释放对象）
delete expr

R
delete[]
deallocate array（释放数组）
delete[] expr

L
->*
ptr to member select（指向成员操作的指针）
ptr ->* ptr_to_member

L
.*
ptr to member select（指向成员操作的指针）
obj .*ptr_to_member

L
*
multiply（乘法）
expr * expr

L
/
divide（除法）
expr / expr

L
%
modulo (remainder)（求模（求余））
expr % expr

L
+
add（加法）
expr + expr

L
-
subtract（减法）
expr - expr

L
<<
bitwise shift left（位左移）
expr << expr

L
>>
bitwise shift right（位右移）
expr >> expr

L
<
less than（小于）
expr < expr

L
<=
less than or equal（小于或等于）
expr <= expr

L
>
greater than（大于）
expr > expr

L
>=
greater than or equal（大于或等于）
expr >= expr

L
==
equality（相等）
expr == expr

L
!=
inequality（不等）
expr != expr

L
&
bitwise AND（位与）
expr & expr

L
^
bitwise XOR（）
expr ^ expr

L
|
bitwise OR（位异或）
expr | expr

L
&&
logical AND（逻辑与）
expr && expr

L
||
logical OR（逻辑或）
expr || expr

R
?:
conditional（条件操作）
expr ? expr : expr

R
=
assignment（赋值操作）
lvalue = expr

R
*=, /=, %=,
compound assign（复合赋值操作）
lvalue += expr, etc.

R
+=, -=,

R
<<=, >>=,

R
&=,|=, ^=

R
throw
throw exception（抛出异常）
throw expr

L
,
comma（逗号）
expr , expr 参考技术B 逗号为从左至右 等号为从右至左 另外就是谁优先的问题 等号优先，自己写个简单程序验证一下 参考技术C ,y=（x=a+b）这一句决定了x和y的值 从右往左算x是5 ，y=x是5 参考技术D 优先的问题.
y=(x=a+b),(b+c)
x=a+b
y=x
x=5,y=5 第5个回答  2012-02-01 主看优先级，赋值优先级高于逗号优先级

蒙特卡洛模拟求解概率统计中的抽奖问题C语言实现

自定义目录名hhh

• 以下是我的正文
• • 0背景重述
  • 1问题
  • 2初始的思路
  • 3编程验证
  • • 3.1算法思路
    • 3.2代码展示
    • 3.3运行结果
  • 4结果分析
  • 5后话
  • 致谢

以下是我的正文

0背景重述

这天我在上大物的时候，坐在我右边的两位室友不停地讨论着什么，我的右耳不时地传来“羊”啊“车”啊的词语。由于我的右耳主要负责捕捉大物老师致睡的声音，左耳朵塞着音乐以堵住知识溜走的去路。人只生有两耳，我便没能听明白室友们到底在讨论啥。于是下课后，我一问，哦，原来是这样……

1问题

室友们在讨论一个概率统计的问题。说一个抽奖活动，参赛者站在三扇门面前，每扇门背后可能是一只羊或是一辆特斯拉（这车现在还有人敢要吗）。羊共有两只，车只有一辆。
参赛者在选择一扇门后（不打开），会有一个人告诉他另外两扇门中有羊的那扇，那么问题来了，参赛者该如何进行第二次选择呢？

2初始的思路

我概率统计没咋学过，对这个问题一开始是这么理解的。一开始选择，什么都不知道，那么选中车的概率就应该是
$$P_{特斯拉}=\frac{1}{3}$$
然后告诉了某扇门后面有只羊，如图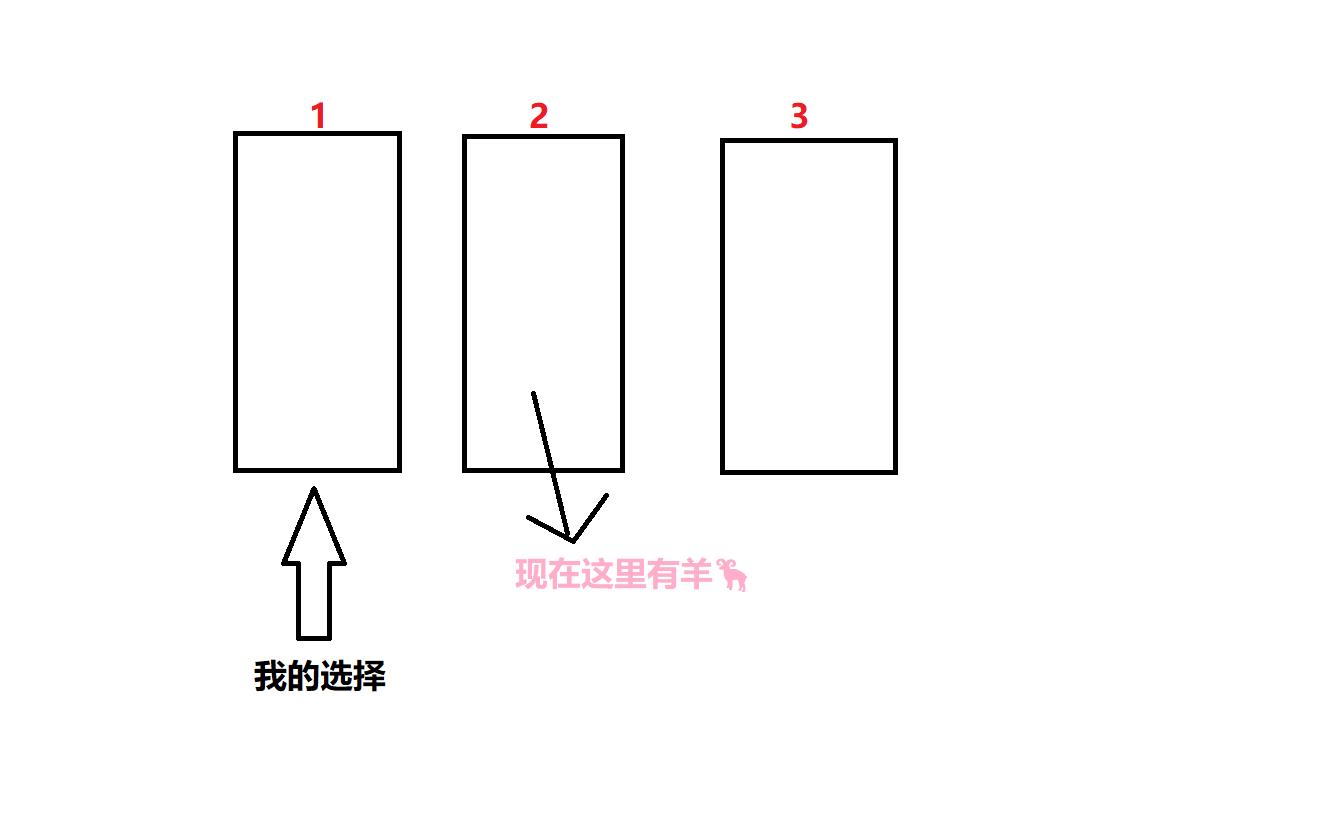
那么现在只剩两扇门了，每扇门背后有车的概率岂不是瞬间变成了
$$P_{特斯拉}=\frac{1}{2}.$$
那我更换选择与否，有用吗？不都是面对当前情形二分之一概率的博弈吗？
事实上，这也正是我其中一位室友的思路，在食堂三楼尊贵的教师餐厅（这里谈笑有鸿儒，往来有杰青）吃饭时，他甚至笃信地对另一位认为更换门后概率变为三分之二的室友说：“绝对是二分之一，如果不是，我给你买金蝉子的皮肤。”
然而真相呢？如何验证呢？另一位室友急了，“等我晚上回去写程序跑跑看。”（下午他们满课）而热爱C语言编程的我当即拍桌，“我回去就去用大数定理模拟一下。”（我下午34才有课）。

3编程验证

3.1算法思路

这种概率问题，我想到的是用蒙特卡洛模拟，据我的理解，就是依据大数定理，对一个实验重复多次后，某一事件的频率即为其概率。
我的算法思路如下：

3.2代码展示

记得先把每个方法看懂，方法命名很好懂的

// 特斯拉与羊
#include<stdio.h>
#include<stdlib.h>
#include<time.h> 
int arr[3];
int FirCatchCount=0;	/*第一次猜中次数*/ 
int AfterChangeCatchCount=0;/*更换后猜中次数*/ 
void InitArray(){ 	// 初始化随机数组
	int carIndex = rand()%3; 
	arr[carIndex]=1; // Tesla
	for (int i=0; i<3; i++){
		if (i==carIndex) continue;
		arr[i]=0; // Sheep
	}
	 
	return;
}

int MyFirstChoose(){	
	int choose = rand()%3;
	return choose;  
}

int FindSheep(int yourChoose){	
	for (int i=0;i<3;++i){
		if (i == yourChoose) continue;
		if (!arr[i]) return i;
	}
}

int MySecondChoose(int firChoose,int sheepIndex){
	for (int i=0;i<3;++i){
		if (i==firChoose||i==sheepIndex) continue;
		return i;
	}
}

void CalculateCount(int firChoose,int secdChoose){
	// 特斯拉标记为1，羊标记为0
	// 所以统计频率时只需要累加数组的值即可
	FirCatchCount+=arr[firChoose];		
	AfterChangeCatchCount+=arr[secdChoose];	
	return;
}

                      /*----程序入口----*/
int main(){
	int TIMES=50000;
	int cnt=0;
	printf("准备开始模拟\\n\\n");
	system("pause"); 
	
		/*蒙塔卡罗模拟*/
	srand((unsigned)time(NULL));	// 播下种子，本段代码最重要的一句，实现真正生成连续随机数 
	do {
		InitArray(); // 初始化随机数组
		int firChoose = MyFirstChoose(); // 进行第一次随机选择 
		int sheepIndex = FindSheep(firChoose); // 告知一只羊的位置 
		int secdChoose = MySecondChoose(firChoose,sheepIndex); // 第二次选择（更换） 
		CalculateCount(firChoose,secdChoose); // 统计次数 
	} while (++cnt<TIMES);
	
	printf("%d次模拟结束。\\n\\n",TIMES);
	system("pause");
	
	printf("坚持第一次选择，选中特斯拉的概率为%lf\\n\\n",FirCatchCount*1.0/TIMES); 
	printf("改变初始选择，选中特斯拉的概率为%lf\\n\\n",AfterChangeCatchCount*1.0/TIMES);
	
	return 0;
} 

我自己在写代码时，主要思考的是如何准确地模拟人做选择、以及上帝视角选羊的过程；但后来发现，如何生成连续的随机数才是更关键的！关于随机数、伪随机数，这里不加赘述，但给一个指路牌，搜索“C语言如何生成连续的随机数”，就可以了解随机数背后的各种机制啦。

3.3运行结果

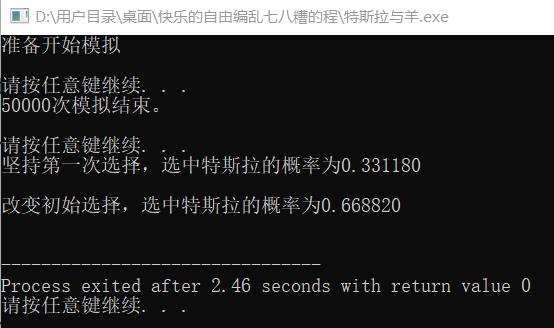
4结果分析

虽然我不知道发生了什么，但是，从结果来看，更换选择后，中奖的概率是坚持第一次选择的两倍！当时把运行结果发到宿舍的微信群里，正在上课的室友估计也露出了上面的表情……

但是用模拟的结果反推机理，思路竟是那样的清晰。

我的顿悟
第一次时啥也不知道，盲选中特斯拉的概率是 $\frac{1}{3}$，这个不会有意见。
然后上帝告诉我们在两扇未选之门中，一扇藏有羊的门的位置，那么我们的选择已经不再是 $3$ 个，而是 $2$ 个了。但是，我们第一次选择的那扇门，中奖的概率不会改变，因为它最初是我们用 $\frac{1}{3}$ 的命中率进行博弈的产物。于是，结果很显然了，更换选择后，有
$$P=1-\frac{1}{3}=\frac{2}{3}.$$
这类问题的核心就是，无论新增了什么条件（告诉你哪扇门后面是羊啊），我们第一次选择的概率始终不会改变，这会成为一个固有属性一直伴随着它。

这就好比当初在万人之中看上了一个女孩，即使有一天，这个世界上只剩下了她和另一个女孩，她仍是万里挑一的她，而不是被二分之一概率选中的她。（？？什么骚话？？）

5后话

紧张的思考过后，随着答案的水落石出，我长舒了一口气，关掉了电脑，走出了宿舍，去教学区上课。下沙校区晴天的下午，阳光还没有灼热到使人有打伞的欲望。微笑地走在路上，溶解于来来往往的学生之中。我一边享受着自己用编程解决问题所带来的乐趣，一边看着微信群里室友的消息。

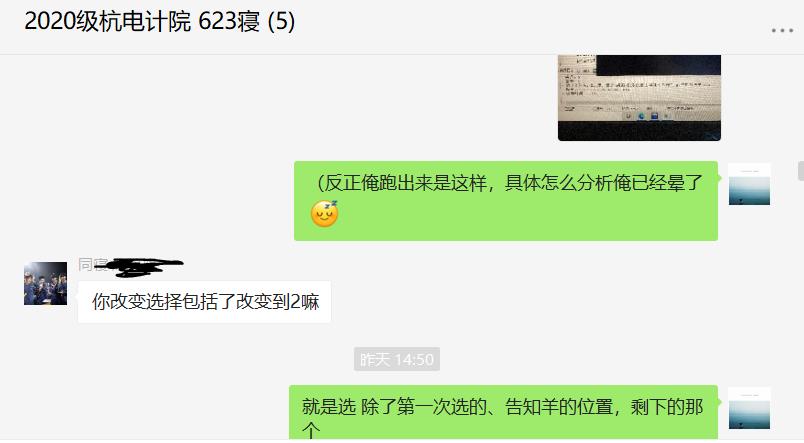
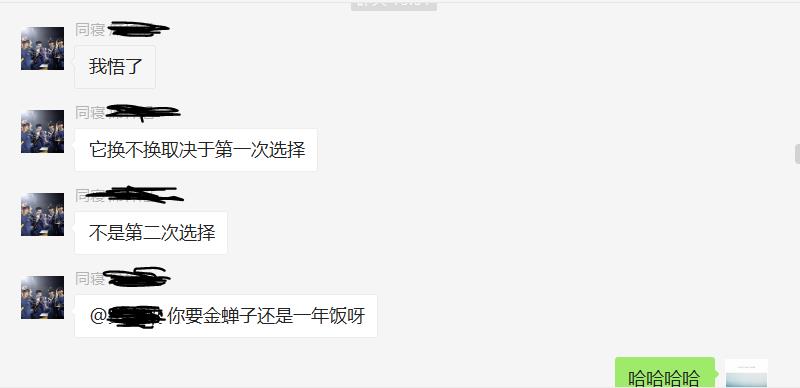
致谢

感谢ZX、XL在大物课上的讨论，否则就不会有这篇文章
感谢TY给的解题的思路
感谢XL在编程思路上给我的启发

感谢你看到这里！如果觉得还有点意思的话，那我就更开心啦哈哈哈