瓦茨瓦夫·谢尔宾斯基的生平

Posted 2023-04-25

参考技术A

波兰数学家，1882年3月14日 生于华沙。1900年进入华沙大学学习，成为沃罗诺伊的学生。1903年华沙大学时，数学物理系设立了一个奖学金，以奖励学生的数论方面的优秀论文。谢尔宾斯基的论文获得了金质奖章，也因此而为他的第一个主要的数学贡献奠定了基础。因为不愿意使用俄语出版，直到1907年，他才将其出版在了萨谬尔·狄克斯坦的数学杂志（The Works of Mathematics and Physics）上。
1904年毕业后，谢尔宾斯基在华沙的一所学校任数学和物理老师。 当学校因为罢工而关闭，谢尔宾斯基决定到克拉科夫攻读博士学位。在克拉科夫的亚格隆尼大学（Jagiellonian University）他做斯塔尼斯瓦夫·萨伦巴（Stanislaw Zaremba）的助教教授数学，同时也学习天文学和哲学。1908年，谢尔宾斯基获得了博士学位并被委派到利沃夫大学。1919年任华沙大学教授。
1907年，当偶然遇到了这样一个理论：平面上的点可以限定一个坐标，他第一次对集合论感兴趣。他写信给塔杜施·巴纳赫维奇（Tadeusz Banachiewicz）（那时在哥廷根），询问他这样的结论怎么可能。他得到的回答只有一个词——格奥尔格·康托尔。1909年，谢尔宾斯基开始研究集合论，他保持着难以置信的研究论文和著作的产出。1908年到1914年，他还是罗乌大学教师时，他出版了三部著作和许多研究论文。这三本著作是：无理数原理（1910年），集合论概论（1912年），数论（1912年）。
1919年，他成为了华沙大学的教授，并在此度过了余生。　1920年，他同齐格蒙特·扬尼舍夫斯基（Zygmunt Janiszewski）以及谢尔宾斯基以前的学生史提芬·马苏基耶维茨（Stefan Mazurkiewicz）三人一起创建了重要的数学刊物《数学基础》（Fundamenta Mathematica）。谢尔宾斯基本人主要负责编辑集合论部分。
在这期间，谢尔宾斯基主要研究集合论，但也研究了点集拓扑学和函数的自由变量。集合论当中，他的贡献主要是选择公理和连续统假设。还有谢尔宾斯基曲线。谢尔宾斯基继续同卢津合作研究分析和投影集合。他研究函数的自由变量包括函数序列（functional series）、函数的导数（differentiability）和Baire's classification。谢尔宾斯基还深刻的影响了数学在波兰的发展。1921年，他成为华沙大学教务长。1928年，他成为华沙科学协会副主席，同年，当选波兰数学协会主席。
第二次世界大战中，在莫斯科被拘留期间，与卢津等俄国数学家接近。1945年回到华沙。1952年被选为波兰科学院院士，曾任该院副院长。还是荷兰、捷克斯洛伐克等外国科学院院士。
长期从事集合论及其在数学名领域(拓扑学、实变函数论等)中应用的研究，就是在第二次世界大战期间也未停止过。对数学的其他领域，特别是数论方面的研究，也取得较大成就。于1906年证明了 ≦1/3这一利用较深的分析方法；1915年又在二维与三维空间给出了“谢尔平斯基缕垫”和“谢尔平斯基海绵”；另提出了“不存在三个有理数，它们的和与积都等於1”的“谢尔平斯基猜想”等。两个著名的分形是根据他的名字命名，谢尔宾斯基三角形和谢尔宾斯基地毯；另外还有谢尔宾斯基数和谢尔宾斯基问题也是以他的名字命名。
谢尔平斯克的著作很多，包括大学教科书、专著和科普读物等，共有700多种。 谢尔平斯克于1920年在华沙与数学家Z·亚尼舍夫斯基和S·马祖凯维奇等人共同创办了《数学基础》杂志，并于1957年恢复出版国际性杂志《算术编年史》。
谢尔平斯克因在数学上的成就，1949年获波兰人民共和国国家奖金，并多次获得其他各种奖金。他1960年时作为华沙大学教授退休，但是仍然继续在华沙科学院的数论方面的研究生课程直到1967年。他仍然继续他的编辑工作，做Acta Arithmetica的责任编辑，还是Rendiconti dei Circolo Matimatico di Palermo、Composito Matematica 和 Zentralblatt für Mathematik 编辑部成员。1969年10月21 日，他在华沙去世，终年87岁。其他著作有《论超穷数》、《数论》、《连续假说》、《一般拓扑学》、《基数和序数》和《数的基础理论》等 。

Python基础——递归及其经典例题（阶乘斐波那契数列汉诺塔）

文章目录

• • 什么是递归
  • 阶乘
  • 斐波那契数列
  • 汉诺塔

---

什么是递归

递归，从原理上讲，就是函数直接或间接地调用自身的算法。是重复调用函数自身实现循环，遇到满足终止条件的情况时逐层返回结束循环，是一种算法结构。

递归在日常编程中有很多例子，例如谢尔宾斯基三角形：

---

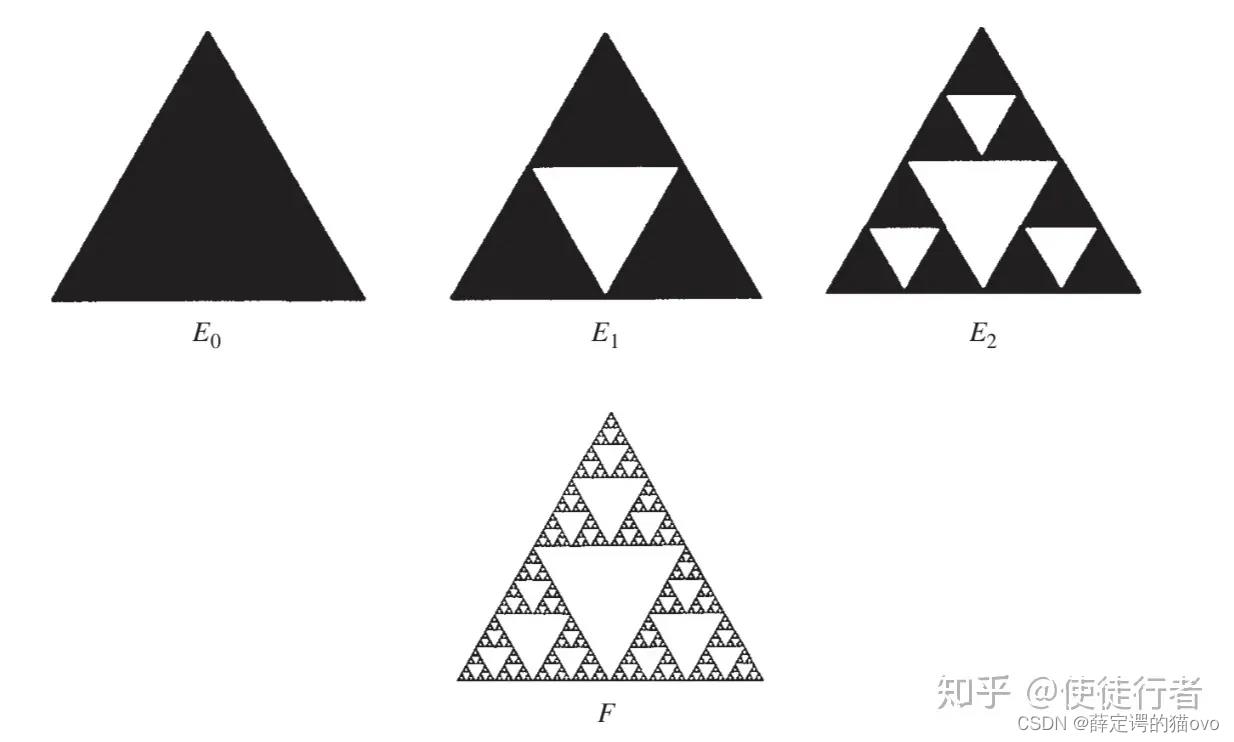
阶乘

正整数的阶乘是指从1乘以2乘以3乘以4一直盛到所要求的的数。例如，所要求的数是5的阶乘，则阶乘式是1×2×3×4×5，得到的积是120，所以120就是5的阶乘。

非递归版本：

# 计算阶乘（非递归）
def recrusion(n):
    result = n
    for i in range(1, n):
        result *= i
    return result

number = int(input('请输入一个整数：'))
result = recrusion(number)
print("%d 的阶乘是：%d" % (number, result))

其执行结果如下：

递归版本：

# 计算阶乘（递归）
def recrusion(n):
    if n == 1:
        return 1
    else:
        return n*recrusion(n-1)

number = int(input('请输入一个整数：'))
result = recrusion(number)
print("%d 的阶乘是：%d" % (number, result))

其执行结果为：

递归函数的实现详细分析如下图所示：

这个例子满足了递归的两个条件：
（1）调用函数本身
（2）设置了正确的返回条件

---

斐波那契数列

再介绍一个递归的经典例题——斐波那契数列。斐波那契数列的发明者，是意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci）。其大致描述是这样的：
假如有一对刚出生的小兔子，只需要一个月小兔子就能长成大兔子，从第三个月开始，这对大兔子每个月都会生下一对小兔子。新出生的小兔子又会花一个月长大，再花一个月开始生兔子…也就是说，兔子在出生两个月后，就有繁殖能力，在拥有繁殖能力后，这对兔子每个月能生出一对小兔子来， 如果每对兔子都经历这样的出生、成熟、生育的过程，并且永远不死，那么每个月兔子的总数是多少呢？

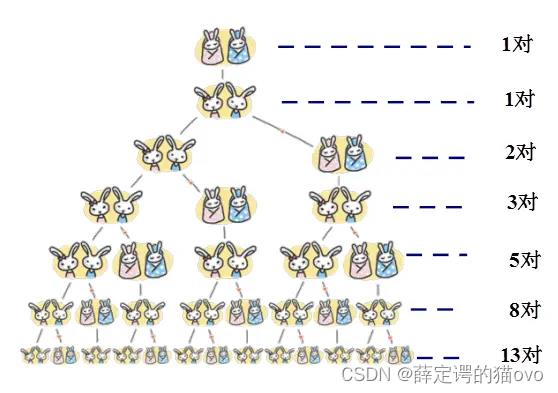
第一个月只有1对兔宝宝。

第二个月只有1对大兔子。

第三个月大兔子生了一对兔宝宝，一大一小2对兔子。

第四个月大兔子继续生一对兔宝宝，小兔子变成大兔子。两大一小3对兔子。

….

于是，我们可以得到每个月兔子的总数：

所经过的月数	1	2	3	4	5	6	7	8	9	10	11	12
1	1	2	3	5	8	13	21	34	55	89	144

可以用数学函数来定义：
$$F(n)=\{\begin{array}{ll}1，& \text{当n=1时}\\ 1，& \text{当n=2时}\\ F(n-1)+F(n-2)，& \text{当n>2时}\end{array}$$

递归实现：

# 实现斐波那契数列
def fab(n):
    if n < 1:
        print('输入有误！')
        return -1
    if n == 1 or n == 2:
        return 1
    else:
        return fab(n-1) + fab(n-2)

result = fab(12)
if result != -1:
    print("第12个月共有%d对兔子" % result)

其执行结果为144。

递归的逻辑很简单，但是递归如果使用不当，效率会很低。因为递归的实现是函数自己调用自身，每次函数的调用都需要进行压栈、出栈、保存和恢复寄存器的操作，所以在这上边是非常消耗时间和空间的。

---

汉诺塔

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

要解决这个问题，其思路如下：
（1）将前63个盘子从A移动到B上，确保大盘在小盘底下。
（2）将最底下的第64个盘子从A移动到C上。
（3）将B上的63个盘子移动到C上。

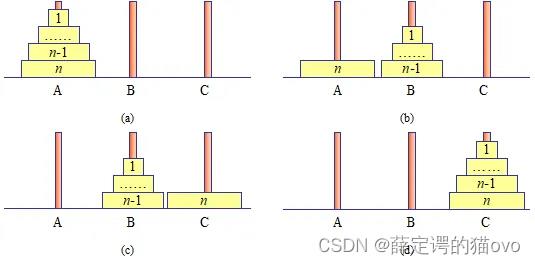
解决问题的思路有了，关键在于步骤（1）和步骤（3）如何执行。由于每次只能移动一个圆盘，所以在移动过程中，显然要借助另外一根针才可以实施。也就是说，步骤（1）将1~63个盘子需要借助C移到B上，步骤（3）将B上的63个盘子借助A移动到C上。

所以，把新的思路聚集为以下两个问题：
问题一：将A上的63个盘子借助C移动到B上；
问题二：将B上的63个盘子借助A移动到C上。

而相应的问题一和问题二的解决方法跟刚才第一个问题的思路是一样的。

问题一（将A上的63个盘子借助C移动到B上）可拆解为：
（1）将前62个盘子从A移动到C上，确保大盘在小盘下。
（2）将最底下的第63个盘子移动到B上。
（3）将C上的62个盘子移动到B上。
问题二（将B上的63个盘子借助A移动到C上）可拆解为：
（1）将前62个盘子从B移动到A上，确保大盘在小盘下。
（2）将最底下的第63个盘子移动到C上。
（3）将A上的62个盘子移动到C上。

所以，这个难题可以用递归来解决：

# 汉诺塔问题
def hanoi(n, a, b, c):  # 将第n层从a借助b移动到c
    if n == 1:
        print(a, '-->', c) # 如果只有一层，直接从a移动到c
    else:
        hanoi(n-1, a, c, b) # 将前n-1个盘子从a移动到b上
        print(a, '-->', c) # 将最底下的第64个盘子从a移动到c上
        hanoi(n-1, b, a ,c) # 将b上的63个盘子移动到c上

n = int(input('请输入汉诺塔的层数：'))
hanoi(n, 'A', 'B', 'C')