三维重建-opencv实现sfm
Posted clxiaoclxiao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了三维重建-opencv实现sfm相关的知识,希望对你有一定的参考价值。
注意:本文中的代码必须使用OpenCV3.0或以上版本进行编译,因为很多函数是3.0以后才加入的。
目录:
SfM介绍
SfM的全称为Structure from Motion,即通过相机的移动来确定目标的空间和几何关系,是三维重建的一种常见方法。它与Kinect这种3D摄像头最大的不同在于,它只需要普通的RGB摄像头即可,因此成本更低廉,且受环境约束较小,在室内和室外均能使用。但是,SfM背后需要复杂的理论和算法做支持,在精度和速度上都还有待提高,所以目前成熟的商业应用并不多。
本系列介绍SfM中的基本原理与算法,借助OpenCV实现一个简易的SfM系统。
小孔相机模型
在计算机视觉中,最常用的相机模型就是小孔模型(小孔成像模型),它将相机的透镜组简化为一个小孔,光线透过小孔在小孔后方的像面上成像,如下图所示。
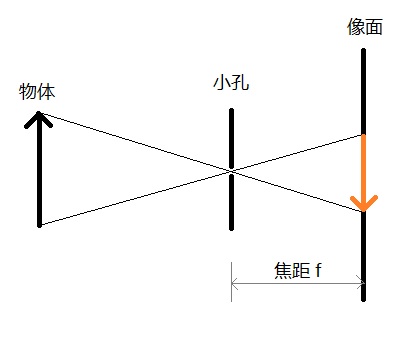
由上图可知,小孔模型成的是倒像,为了表述与研究的方便,我们常常将像面至于小孔之前,且到小孔的距离仍然是焦距f,这样的模型与原来的小孔模型是等价的,只不过成的是正像,符合人的直观感受。在这种情况下,往往将小孔称作光心(Optical Center)。
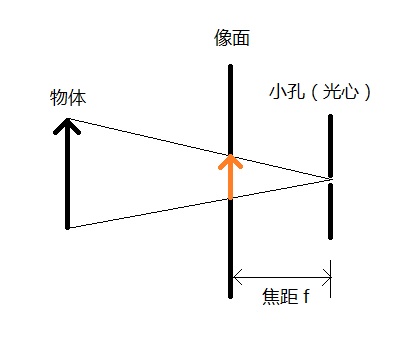
小孔模型是一种理想相机模型,没有考虑实际相机中存在的场曲、畸变等问题。在实际使用时,这些问题可以通过在标定的过程中引入畸变参数解决,所以小孔模型仍然是目前最广泛使用的相机模型。
坐标系
为了用数学研究SfM,我们需要坐标系。在SfM中主要有两类坐标系,一类为相机坐标系,一类为世界坐标系。在本系列中,所以坐标系均为右手坐标系。
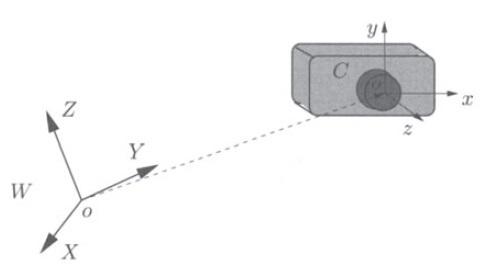
相机坐标系以相机的光心(小孔)作为原点,X轴为水平方向,Y轴为竖直方向,Z轴指向相机所观察的方向。
世界坐标系的原点可以任意选择,与相机的具体位置无关。
内参矩阵
设空间中有一点P,若世界坐标系与相机坐标系重合,则该点在空间中的坐标为(X, Y, Z),其中Z为该点到相机光心的垂直距离。设该点在像面上的像为点p,像素坐标为(x, y),那么(X, Y, Z)和(x, y)有什么关系呢?
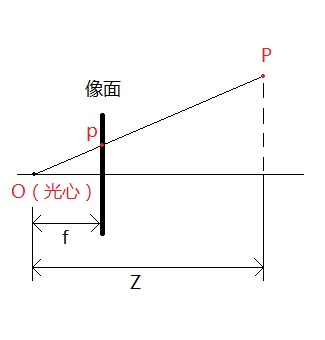
由上图可知,这是一个简单的相似三角形关系,从而得到
但是,图像的像素坐标系原点在左上角,而上面公式假定原点在图像中心,为了处理这一偏移,设光心在图像上对应的像素坐标为 (cx,cy) ,则
x=fXZ+cx, y=fYZ+cy
将以上关系表示为矩阵形式,有
Zxy1=f000f0cxcy1XYZ
其中,将矩阵
K=f000f0cxcy1
称为内参矩阵,因为它只和相机自身的内部参数有关(焦距,光心位置)。
外参矩阵
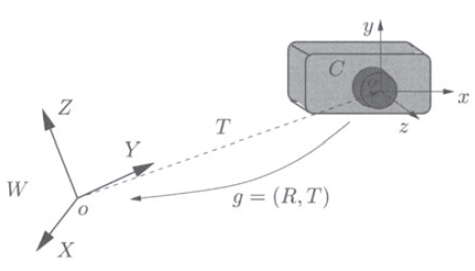
一般情况下,世界坐标系和相机坐标系不重合,这时,世界坐标系中的某一点P要投影到像面上时,先要将该点的坐标转换到相机坐标系下。设P在世界坐标系中的坐标为X,P到光心的垂直距离为s(即上文中的Z),在像面上的坐标为x,世界坐标系与相机坐标系之间的相对旋转为矩阵R(R是一个三行三列的旋转矩阵),相对位移为向量T(三行一列),则
其中 RX+T 即为P在相机坐标系下的坐标,使用齐次坐标改写上式,有
sx=K[RT][X1]
其中 [RT] 是一个三行四列的矩阵,称为外参矩阵,它和相机的参数无关,只与相机在世界坐标系中的位置有关。
相机的标定
相机的标定,即为通过某个已知的目标,求取相机内参矩阵的过程。最常用的标定目标就是棋盘格。用相机对棋盘格从不同角度拍摄多张照片,然后将这些照片导入标定程序或算法,即可自动求出相机的内参。
相机标定的方法和工具,我在这篇文章中已有详细的介绍,这里就不再细述了。在此提醒一下,之后的文章中若无特殊说明,所有相机均假定内参已知。
目录:
极线约束与本征矩阵
在三维重建前,我们先研究一下同一点在两个相机中的像的关系。假设在世界坐标系中有一点 p ,坐标为 X ,它在1相机中的像为 x1 ,在2相机中的像为 x2 (注意 x1 和 xECCV2020优秀论文汇总|涉及点云处理3D检测识别三维重建立体视觉姿态估计深度估计SFM等方向