基于Δ-Σ模数转换器的梳状滤波器的设计与matlab仿真
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于Δ-Σ模数转换器的梳状滤波器的设计与matlab仿真相关的知识,希望对你有一定的参考价值。
欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》
目录
一、理论基础
Δ-Σ模数转换器是一种低速,高精度的过采样模数转换器广泛的应用于信号采集和处理、数字通信、自动检测、自动控制和多媒体技术等领域。作为Δ-Σ模数转换器首级的梳状滤波器的设计就显得非常重要,滤波器的设计直接决定了整个芯片的面积和功耗却是由滤波器部分来决定的。
Δ-Σ数模转换器是由数字插值滤波器、数字Sigma-Delta调制器和模拟低通滤波器组成。数字插值滤波器是将奈奎斯特采样信号转换为过采样信号,数字Sigma-Delta调制器是将过采样信号进行噪声整形,而模拟低通滤波器是用来滤除基带以外的信号噪声并将调制器输出信号重构为连续时间域的模拟信号。关于Δ-Σ模数、数模转换器的基本原理与结构将在第二章节中详细介绍。其基本结果如下所示:
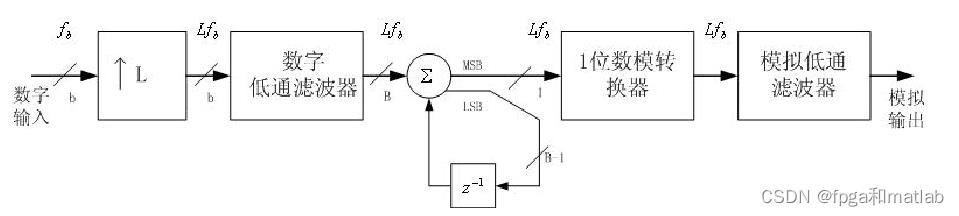
Δ-Σ模数转换器是一种高分辨率的数据转换器,目前正广泛应用于高保真数字处理系统中,作为Δ-Σ模数转换器首级的梳状滤波器的设计就显得非常重要。高速A/D采样得到中频数字信号,将其所需的频带下变到基带,它一般位于信号处理链的前端A/D,主要有数字振荡器(VCO)、数字乘法器、数字滤波器三部分组成。
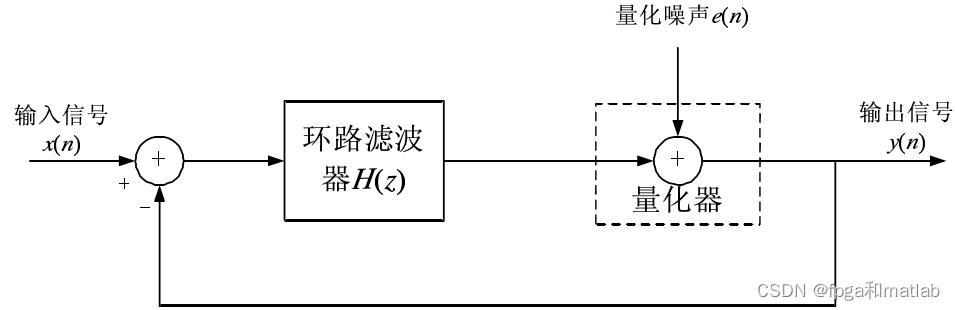
Σ-Δ调制器的基本原理可以概括为利用过采样降低噪声功率在信号频带内的分布,在此基础上再利用噪声整形进一步抑制带内噪声,从而提高带内信号的信噪比。Σ-Δ调制器的基本结构如图2。在假设量化噪声e(n)是白噪声的情况下,输入信号x(n)和量化噪声是e(n)是量化器的两个相互无关的输入,因此量化器的输出可等效为输入信号和量化噪声的叠加。
假设用N级CIC滤波器来代替hn,每一级的滤波器系数长度为R,每一级的差分延迟为M,抽取数为R,那么可以得到CIC抽取滤波器结构图:
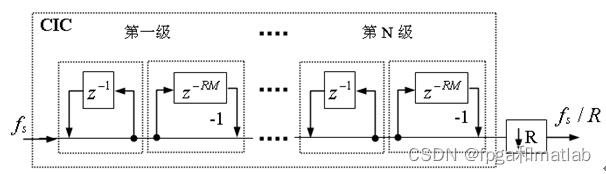
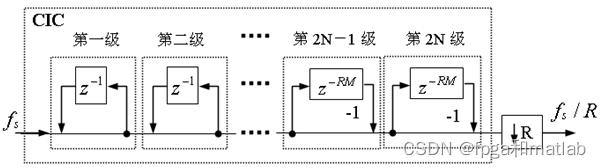
N级CIC滤波器在功能上相当于N级完全相同的FIR滤波器的级联。如果按传统的FIR滤波器方式实现,那么N级FIR滤波器的每一级都需要RM个存储单元和一个累加器,但如果用CIC方式实现,那么N级CIC滤波器的每一级只需要M个存储单元。
二、核心程序
clc;
clear;
close all;
%CIC滤波器的参数
R = 32; %抽取因子
M = 1; %延迟
N = 5; %CIC阶数
B = 8; %有限字长
Fs = 10.24e6; %信号的频率
Fc = 20e3; %信号带宽
%FIR
L = 30; %滤波器的阶数
Fo = R*Fc/Fs;
%% FIR
p = 2e3;
s = 0.25/p;
fp = [0:s:Fo];
fs = (Fo+s):s:0.5;
f = [fp fs]*2;
Mp = ones(1,length(fp));
Mp(2:end) = abs( M*R*sin(pi*fp(2:end)/R)./sin(pi*M*fp(2:end))).^N;
Mf = [Mp zeros(1,length(fs))];
f(end) = 1;
h = fir2(L,f,Mf);
h = h/norm(h);
hz = floor(h*power(2,B));
%% CIC
hrec = ones(1,R*M);
tmph = hrec;
for k=1:N-1
tmph = conv(hrec, tmph);
end;
hcic = tmph;
hcic=hcic/norm(hcic);
%%
hzp = upsample(hz,R);
hp = upsample(h, R);
ht = conv(hcic, hp);
hzt = conv(hcic, hzp);
[Hcic, wt] = freqz(hcic, 1, 4096, Fs);
[Hciccomp, wt] = freqz(hp, 1, 4096, Fs);
[Ht, wt] = freqz(ht, 1, 4096, Fs);
[Hzt, wt] = freqz(hzt, 1, 4096, Fs);
Mcic = 20*log10(abs(Hcic)/max(abs(Hcic)));
Mciccomp = 20*log10(abs(Hciccomp)/max(abs(Hciccomp)));
Mt = 20*log10(abs(Ht)/max(abs(Ht)));
Mzt = 20*log10(abs(Hzt)/max(abs(Hzt)));
%%
figure;
plot(wt, Mcic);
legend('CIC');
grid
xlabel('频率');
ylabel('幅度');
figure
plot(wt, Mt,wt, Mzt);
legend('Total Response (Floating Point)','Total Response Fixed Point')
grid
xlabel('频率');
ylabel('幅度');
title('浮点仿真与定点仿真');
clc;
clear;
close all;
K=500;%仿真时间
k=0:1:K;
w=pi*k/K;
R=1;
M=input('Please input M:');%抽取32
N=input('Please input N:');%滤波器的级数
num=sin(R*M*w/2);
den=sin(w/2)+eps;
H=(num./den).^N;
magH=abs(H);
angH=-1/2*(R*M-1)*N*w;
magH=20*log10(magH+eps);
subplot(2,1,1)
plot(w/pi,magH);grid on;
axis([0,1,-200,300]);
xlabel('frequency in pi units');
ylabel('|H|');
title('Magnitude Response(db)');
subplot(2,1,2);
plot(w/pi,angH/pi);grid on;
xlabel('frequency in pi units');
ylabel('Phase in pi Radians');
title('Phase Response');
三、测试结果
不同阶数的单级CIC梳状滤波器的幅频特性曲线。
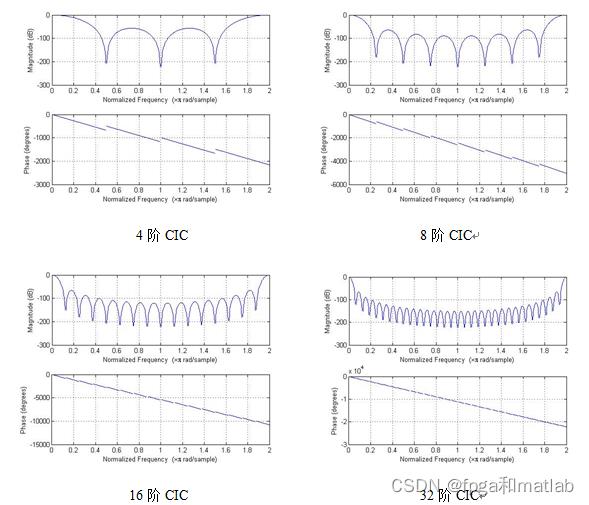
测试的输入信号频率为10.24MHz,基带信号带宽为20KHz。我们将这个输入信号作为测试信号,对滤波器进行测试。通过CIC滤波之后,其仿真结果如下所示:
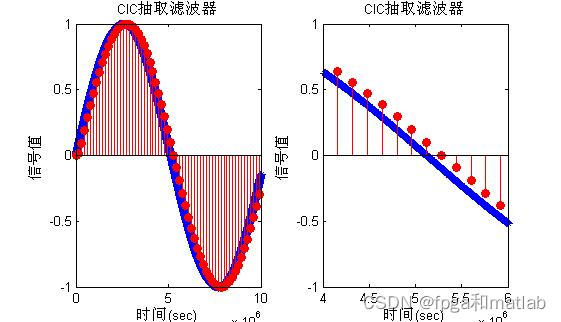
下面考虑梳状滤波器的三个参数变量进行并结合实际的工作环境进行综合仿真,在实际的ADC中,往往会在CIC滤波器之后加入一个FIR滤波器作为补偿滤波器。
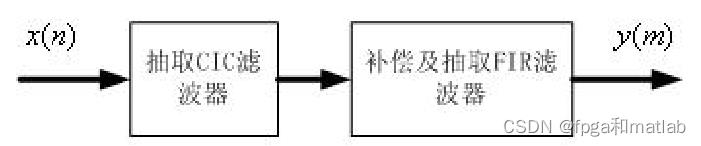
通过仿真,可以看到其仿真结果如下所示:
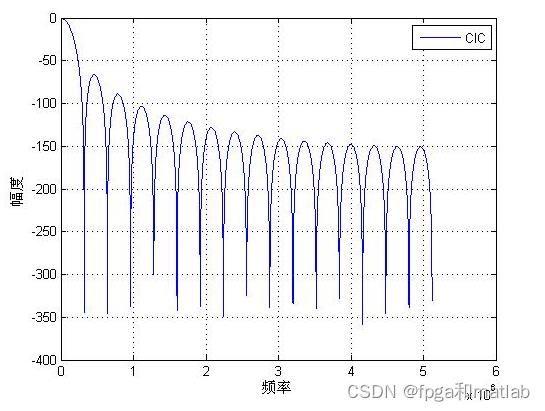
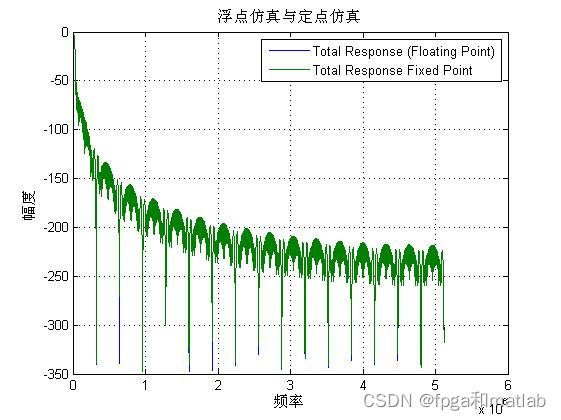
图4 数据字长为32的浮点定点仿真对比图
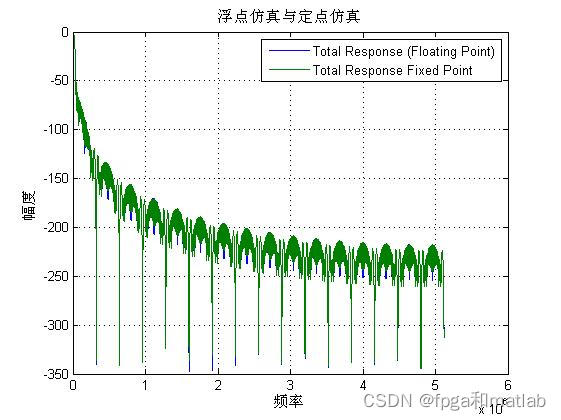
图5 数据字长为16的浮点定点仿真对比图
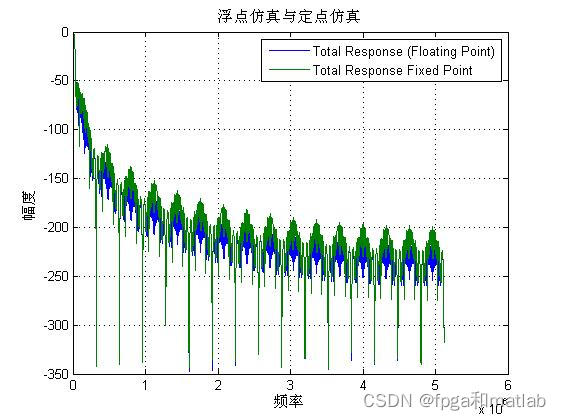
当数据字长为8的时候,浮点仿真结果和定点仿真结果具有较大的误差,而参数选择为16和32的时候,两者之间的误差较小。当考虑硬件资源的时候,我们选择字长为16。A25-03。
以上是关于基于Δ-Σ模数转换器的梳状滤波器的设计与matlab仿真的主要内容,如果未能解决你的问题,请参考以下文章