去除杂波的梳状滤波器

Posted 2022-05-26 卓晴

简 介： 本文分析了两种可以去除周期干扰信号的滤波器，一个是周期平滑滤波器，它可以彻底去除信号中周期信号，但滤波器同时对信号中高频分量与也有较大的衰减。 另一个是延迟相加滤波器，它比较接近于理想的梳状滤波器，但这种滤波器只能去除满足奇谐对称的交流分量。 在实际应用中需要根据信号的特点分别选择不同的梳状滤波器。

关键词： 滤波器，梳状滤波器

 

§01 梳状滤波器

---

一、系统函数与频率特性

  本周的信号与系统课程讲解了系统变换域分析。作为最后的一个重点内容，系统函数的零极点对系统频率特性影响是课程的难点，主要是针对原来理论上关于系统函数在复平面虚轴上的取值（离散时间系统在复平面单位圆上的取值）表征了系统的频率特性。

• 幅频特性： $\left|H_C\left(j\omega \right)\right|,\left|H_D\left(e^{j\omega }\right)\right|$
• 相频特性： $\angle H_C\left(j\omega \right),\angle H_D\left(e^{j\omega }\right)$

  通常情况下我们关注较多的幅频特性将系统分为以下多种系统（一连续时间系统为例）

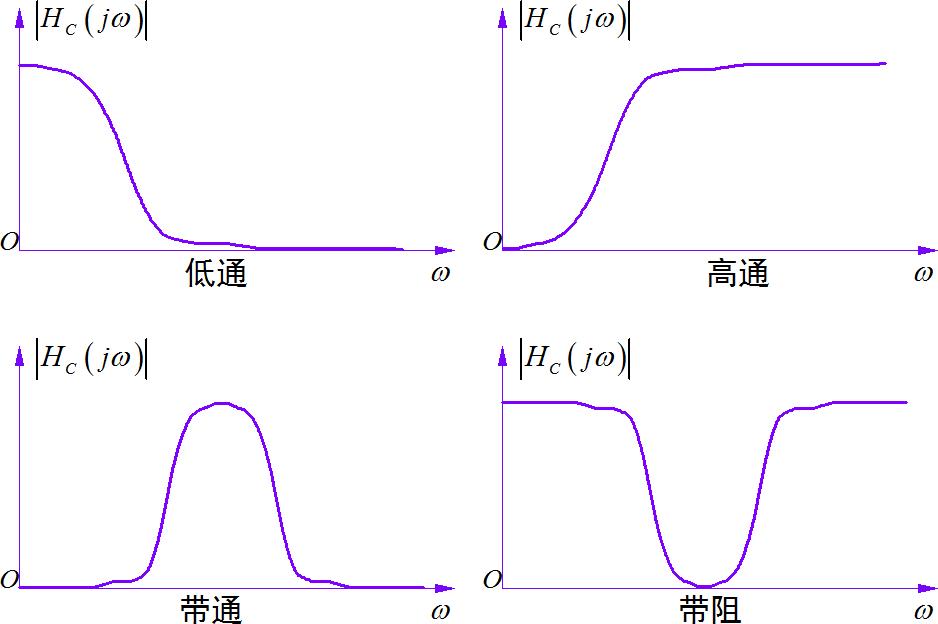
▲ 图1.1.1 基本滤波器类型

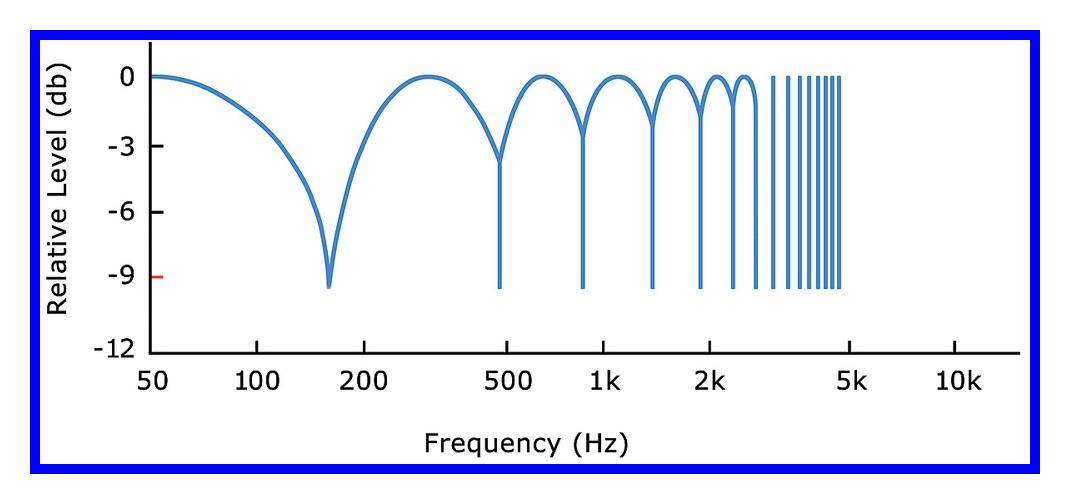
  系统的频率特性主要是由系统函数中靠近虚轴的零点和极点分布决定。 靠近虚轴的极点会在系统幅频特性对应的极点虚部频率处产生峰值；反之靠近虚轴的零点会在系统幅频特性对应极点虚部频率处产生下降凹陷。下面从实际问题出发，介绍一个特殊的滤波器“ 梳状滤波器（Comb Filter） ” 。这种梳状滤波器会在虚轴上分布周期的零点，进而可以把某一频率信号及其谐波信号进行除去。

二、滤除谐波干扰

  参加全国大学竞赛的同学经常会询问一个问题：如何 进行磁铁检测 ？ 在使用 干簧管、霍尔、线圈 等检测方式中，使用线圈检测永磁铁灵敏度最高，检测距离可以超过10厘米。下面是永磁铁检测线圈及其信号单电源放大电路。

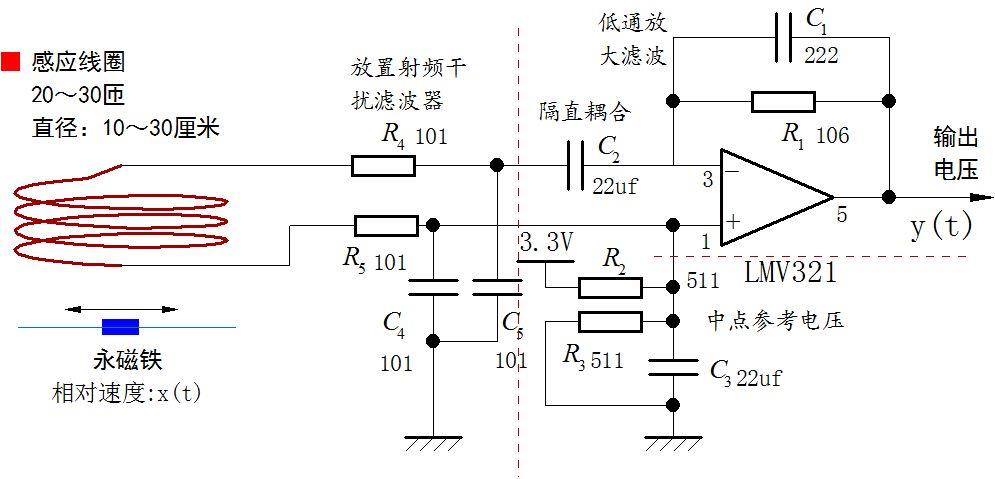
▲ 图1.2.1 . 永磁铁检测线圈以及信号放大电路

  但使用检测线圈时勋在一个最大的问题，就是放大后的信号中存在着较大的工频干扰信号。这些干扰信号来自于我们房间中存在着市电工频干扰。下图现实了检测线圈以及在静止状态下滤波放大后的信号。

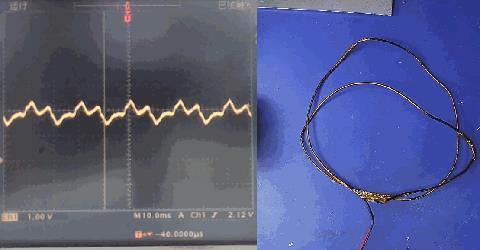
▲ 图1.2.2 感应线圈滤波放大后的信号

  这个信号不是一个纯正弦波，所以它除了50Hz的基频之外，还有很多的高次谐波分量。下图是利用数字示波器采集到的放大器的输出信号数据，在MATLAB中利用FFT得到的信号频谱，可以看到其中存在的各个谐波分量。信号谐波分量还有一个特点，就是奇次谐波（50Hz, 150Hz, 250Hz等）幅值比较大， 偶次谐波（100Hz，200Hz，300Hz等）幅值很小。这个特性是由干扰谐波满足“奇谐对称”有关系， 也就是信号时间延迟半个周期，其中的交流分量恰好极性相反。

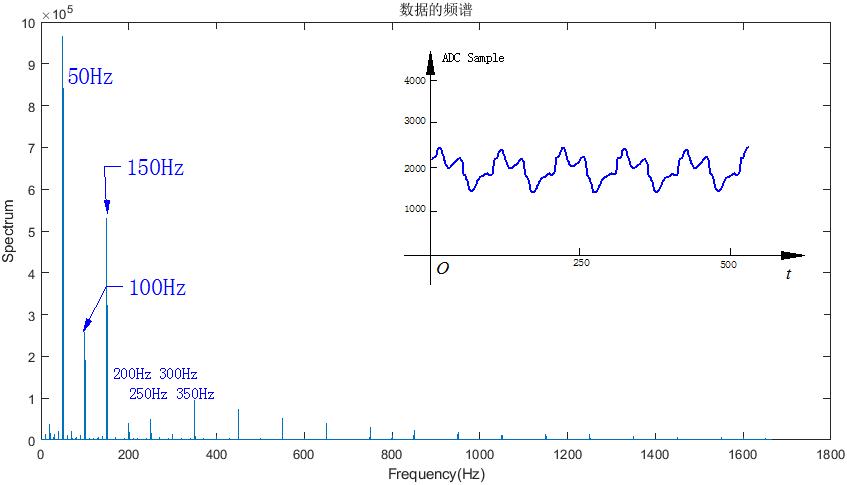
▲ 图1.2.3 利用MATLAB计算出信号中的各个谐波分量

三、梳状滤波器

  如果去除上述干扰信号，同时尽可能保留原来信号的频率分量， 使用梳状滤波器最合适。所谓梳状滤波器就是他的幅频特性出现周期性的“凹陷”，将对应的频率分量进行衰减。 在信号处理中，常见到的梳妆滤波算法包含以下两种。

1、周期平滑滤波

  这是在实践中常用到的方法，就是对信号的一个周期内（或者几个周期内）的数据进行累加平均，这样信号中的周期干扰信号就会被平滑衰减。 从数学上来看，周期平滑滤波相当于信号 $f\left(t\right)$ 与矩形信号 $h\left(t\right)=\frac{1}{T_0}\left[u\left(t\right)-u\left(t-t_0\right)\right]$ 卷积，得到平滑后的信号 $f_{average}\left(t\right)$ ： $$f_{average}\left(t\right)=h\left(t\right)\ast f\left(t\right)=\frac{1}{T_0}{\int }_{t-T_0}^{t}f\left(\tau \right)d\tau$$

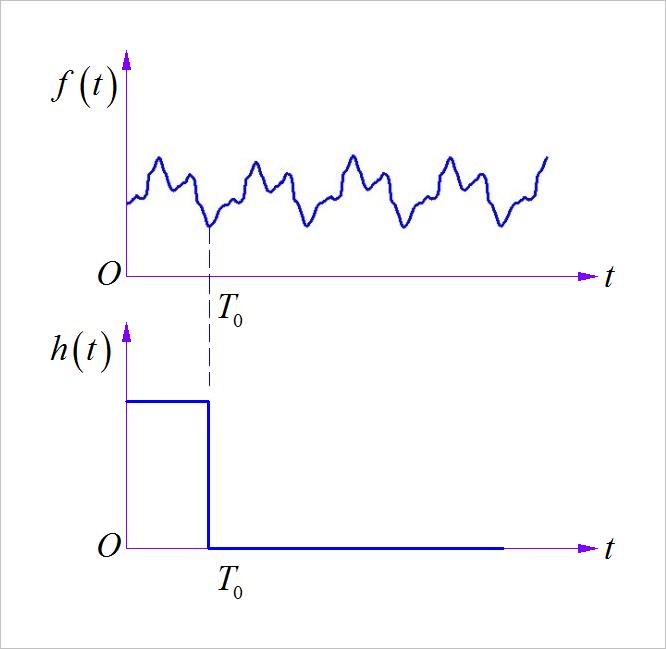
▲ 图1.3.1 信号f(t)与滤波器信号h(t)

  周期平滑滤波器对应的系统函数为 $$H\left(j\omega \right)=\frac{1}{s}\left(1-e^{-s{T}_0}\right)$$ 对应的幅频特性和系统零极点分布如下图所示。 可以看到系统中的零点周期分布在虚轴上， 间隔为 ${\omega }_0=2\pi /T_0$ 。在原点处的极点和零点发生了抵消。

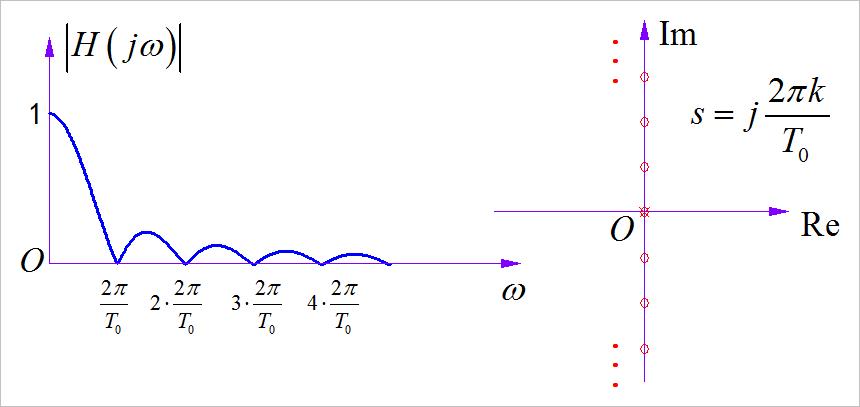
▲ 图1.3.2 周期平滑滤波器的幅频特性与零极点分布

  设置 $T_0$ 等于 50Hz 周期或者周期的整数倍数，那么就可以把50Hz的周期干扰信号彻底清除干净。

  但是上述滤波器有一个缺点，就是它不仅率除了谐波干扰，同时对于信号中的高频分量也进行了衰减，这句是理想的梳状滤波器差别比较大。

2、延迟叠加滤波器

  上述平滑滤波器之所以出现高频衰减，就是因为在传递函数中出现了分母上的 $s$ ， 如果将分母上的 $s$ 去掉，系统函数变成了 $H\left(s\right)=1-e^{-s{T}_0}$ ，此时系统的幅频特性和零极点分布如下。 不过可以看出，这个滤波器不仅去掉了周期信号的各个谐波分量，同时直流分量也没有被保存，这不适合于前面永磁铁检测线圈。

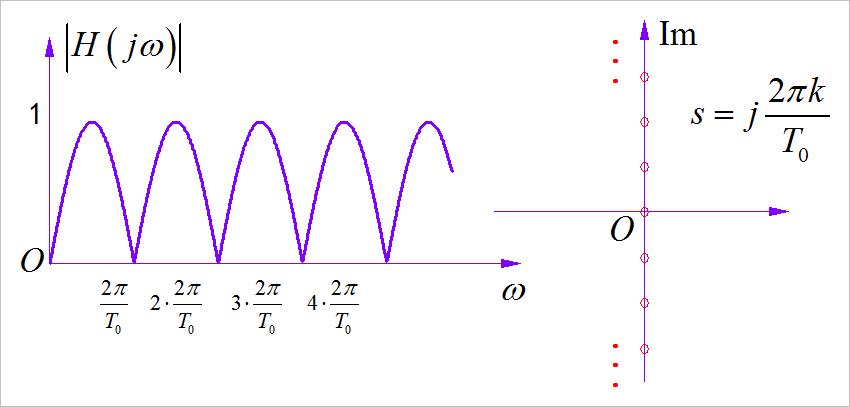
▲ 图1.3.3 延时相减滤波器及其零极点分布

  因为磁铁运动所产生的的电压分量属于缓慢变化的信号，上述滤波器需要进行改造，将其中的减号编程加号。
$$H\left(s\right)=1+e^{-s{T}_0}$$ 对应的幅频特性和零极点分布如下。可以看到此时系统的直流增益就不在是0了。

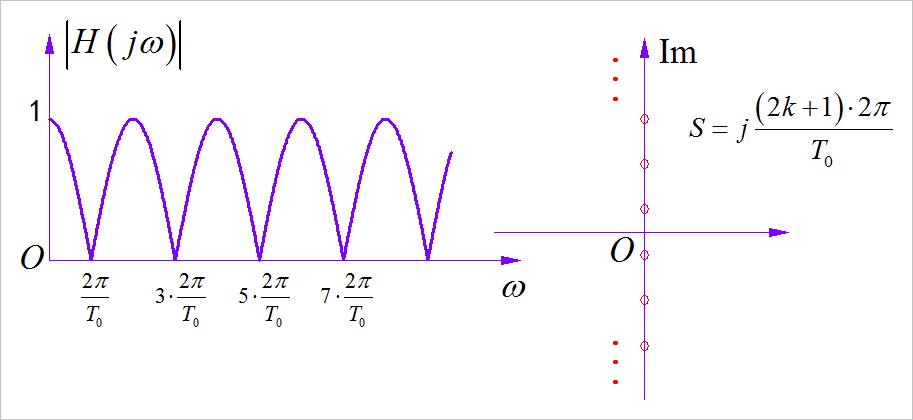
▲ 图1.3.4 延时相加滤波器及其零极点分布

  上述系统函数对应的是一个延迟相加系统，也就是把信号与它的延迟累加。 系统框图如下图所示。

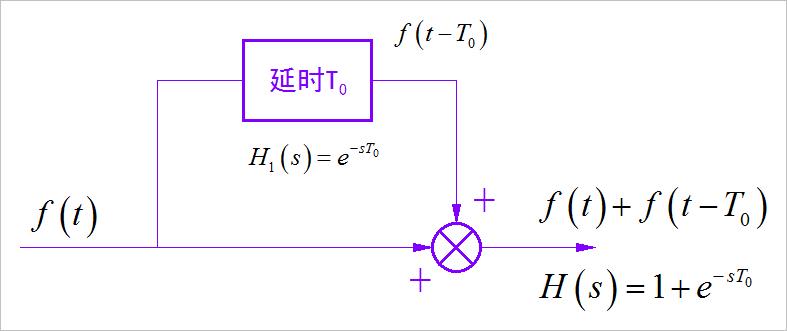
▲ 图1.3.5 滤波器对应的延迟相加系统

  通过观察延迟相加系统的零极点分布，可以看到，为了使得滤波器系统函数第一个零点对准周期信号的基频，那么其它的零点则对应周期信号的奇次谐波，而偶次谐波对应的频率则不是零点。因此，这种滤波器虽然比较靠近梳装滤波器，但只能滤除谐波中的奇次分量，所以这种滤波器对于奇谐对称的交流信号有很好的滤除作用。

  上面电磁检测线圈中的市电干扰信号就基本上满足奇谐对称，所以使用延迟相加所形成的的梳状滤波器也可以去除其中的交流噪声信号。

 

※ 总 结 ※

---

  本文分析了两种可以去除周期干扰信号的滤波器，一个是周期平滑滤波器，它可以彻底去除信号中周期信号，但滤波器同时对信号中高频分量与也有较大的衰减。 另一个是延迟相加滤波器，它比较接近于理想的梳状滤波器，但这种滤波器只能去除满足奇谐对称的交流分量。 在实际应用中需要根据信号的特点分别选择不同的梳状滤波器。

---

■ 相关文献链接:

• 梳状滤波器（Comb Filter）
• 全国大学竞赛
• 进行磁铁检测
• 干簧管的可靠检测

● 相关图表链接:

• 图1.1.1 基本滤波器类型
• 图1.2.1 . 永磁铁检测线圈以及信号放大电路
• 图1.2.2 感应线圈滤波放大后的信号
• 图1.2.3 利用MATLAB计算出信号中的各个谐波分量
• 图1.3.1 信号f(t)与滤波器信号h(t)
• 图1.3.2 周期平滑滤波器的幅频特性与零极点分布
• 图1.3.3 延时相减滤波器及其零极点分布
• 图1.3.4 延时相加滤波器及其零极点分布
• 图1.3.5 滤波器对应的延迟相加系统

开发者涨薪指南 48位大咖的思考法则、工作方式、逻辑体系