DP. 数字三角形模型

Posted 2022-11-28 Debroon

DP.数字三角形模型

• • 1015. 摘花生
  • 1018. 最低通行费
  • 1027. 方格取数
  • 275. 传纸条

 

---

1015. 摘花生

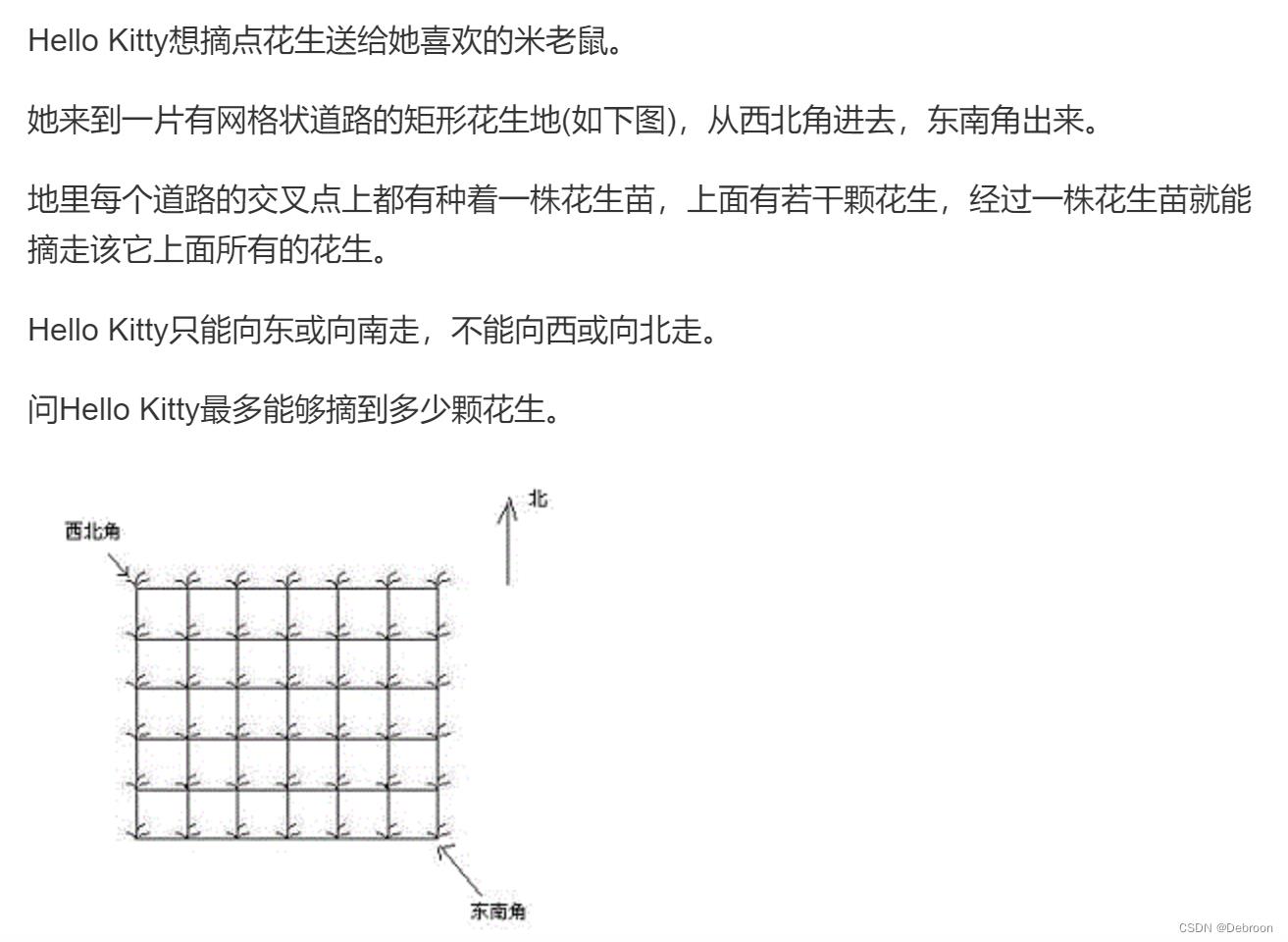
终点：

• 东南角 $(i,j)$
• 设东南角最大花生数 dp[i][j]

那 dp[i][j]，从哪里来？

• 可能一：左边 dp[i-1][j]
• 可能二：上边 dp[i][j-1]
• 转移方程：$dp[i][j]=max(dp[i-1][j]+w[i][j],dp[i][j-1]+w[i][j])$
• 最简单的情况：$dp[0][0]=0$

第 i 层的答案只依赖于第 i 层和第 i - 1 层，可以状态压缩。

• 转移方程：$f[j]=max(f[j],f[j-1])+w$
   

---

1018. 最低通行费

因为从方格左上角走到右下角的距离是：N*N，要在 2N-1 的时间出去，这代表不能走回头路。

在这个限定条件下，整体思路\\代码和摘花生没有区别。
 

---

1027. 方格取数

一开始的思路就是，俩次 DP 即可。

但是分开走的局部最优，不是全局最优。

从 A 点到 B 点共走了两次，我们可以设两条路径是同时出发的。

因为是俩条路径，我们用俩维数组是存不下的，我们开四维的。

走法还是不能走回头路，俩个方向 * 俩个走法 = 4。

按照题目要求，还需要在刷新值，第一次走过的格子要变成 0。

        for (int a = 1; a < n; a++) 
            for (int b = 1; b < n; b++) 
                for (int c = 1; c < n; c++) 
                    for (int d = 1; d < n; d++) 
                        int x = max(f[a - 1][b][c - 1][d], f[a - 1][b][c][d - 1]);
                        int y = max(f[a][b - 1][c - 1][d], f[a][b - 1][c][d - 1]);
                        int z = g[a][b] + ((a == c && b == d) ? 0 : g[c][d]); // 是否走同一个格子，同一个格子只能走一次，第二次赋值为 0 
                        f[a][b][c][d] = max(x, y) + z;
                    
        return f[n - 1][n - 1][n - 1][n - 1];

 

---

275. 传纸条

从小渊传到小轩的纸条只可以向下或者向右传递，小轩传给小渊的纸条只可以向上或者向左传递。

可是这并不影响结果，因为任意一个从点 $(m,n)$ 到点 $(1,1)$ 的路径都可以映射成一个从点 $(1,1)$ 到点 $(m,n)$ 的路径。

这样就和方格取数相同了。

与方格取数不同的是, 一个方格只能经过一次（每个同学只帮一次）。