动态规划数字三角形模型 AcWing 1027. 方格取数 275. 传纸条

Posted 2021-05-18 尘封陌路

思路：

不能分开走

分开两次走（贪心）：第一次走到（n，n）求除最大值并记录路径上点收益为0后再走一次。

第一次走为局部最优并且也对第二次走造成了影响，第二次走是在第一次影响下所能走的局部最优，不具备“无后效性”，因此分开两次走并不是全局最优解。

解法：

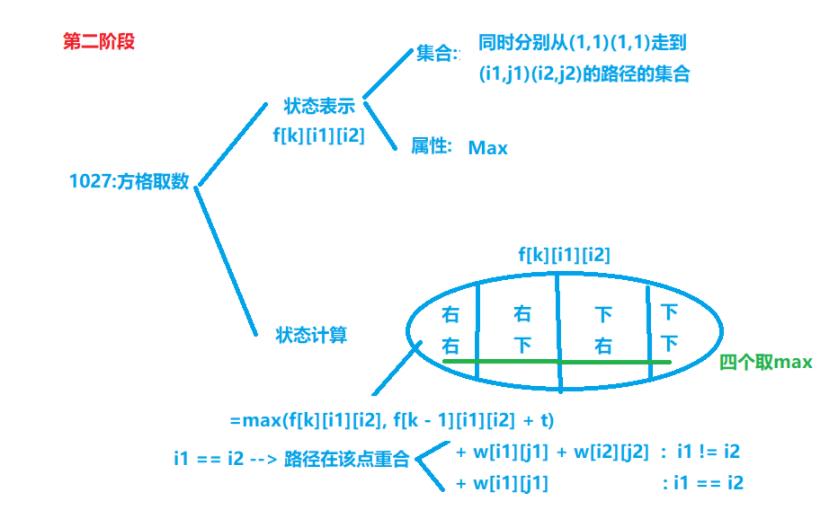
代码如下：

//方格取数 
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int f[N][N][N];
int n;
int g[N][N];
int main()
{
	cin>>n;
	int a,b,c;
	while(cin>>a>>b>>c)
	{
		if(a==0&&b==0&&c==0)
		{
			break;
		}
		g[a][b]=c;
	}
	for(int k=2;k<=n+n;k++)
	{
		for(int i1=1;i1<=n;i1++)
		{
			for(int i2=1;i2<=n;i2++)
			{
				int j1=k-i1;
				int j2=k-i2;
				if(j1>=1&&j1<=n&&j2>=1&&j2<=n)
				{
					int w=g[i1][j1];
					if(i1!=i2) w+=g[i2][j2];
					int& x=f[k][i1][i2];
					x=max(x,f[k-1][i1-1][i2-1]+w);
					x=max(x,f[k-1][i1-1][i2]+w);
					x=max(x,f[k-1][i1][i2-1]+w);
					x=max(x,f[k-1][i1][i2]+w);
				}
			}
		}
	}
	
	cout<<f[n+n][n][n]<<endl;
	return 0;
}

//传纸条 
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int f[N][N][N];
int n,m;
int g[N][N];
int main()
{
	cin>>n>>m;
	int a,b,c;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>g[i][j];
		}
	}
	for(int k=2;k<=n+m;k++)
	{
		for(int i1=1;i1<=n;i1++)
		{
			for(int i2=1;i2<=n;i2++)
			{
				int j1=k-i1;
				int j2=k-i2;
				if(j1>=1&&j1<=m&&j2>=1&&j2<=m)
				{
					int w=g[i1][j1];
					if(i1!=i2) w+=g[i2][j2];
					int& x=f[k][i1][i2];
					x=max(x,f[k-1][i1-1][i2-1]+w);
					x=max(x,f[k-1][i1-1][i2]+w);
					x=max(x,f[k-1][i1][i2-1]+w);
					x=max(x,f[k-1][i1][i2]+w);
				}
			}
		}
	}
	
	cout<<f[n+m][n][n]<<endl;
	return 0;
}